03 Trigo

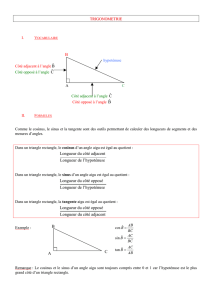
CH III Cosinus, sinus et tangente d'un angle aigu d'un triangle rectangle
!
1. Activité : Découverte des trois rapports trigonométriques
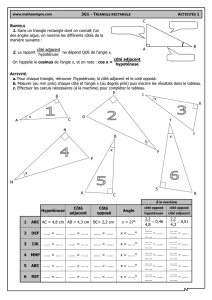
• Voici deux triangles qui ont les mêmes angles.
!
!
!
!
• On peut donc mettre le plus petit à l'intérieur du plus grand. Je les appelle ABC et AB1C1.
!
!
!
!
!
!
!
• Je vois que (BC) // (B1C1). C'est une certitude en utilisant le théorème suivant :
SI deux droites sont toutes deux perpendiculaires à une même troisième droite
LORS elles sont parallèles.
!
• Toutes les conditions sont requises pour utiliser le théorème de Thalès :
Les deux triangles ont leurs longueurs de côté proportionnelles.
!
• Donc :
!
! = ! = ! = ! ou hypoténuse x ! = côté adjacent
Le cosinus est le multiplicateur qui permet de passer de l'hypoténuse au côté adjacent.
C'est un nombre inférieur à 1.
!
! = ! = ! = ! ou hypoténuse x ! = côté opposé
Le sinus est le multiplicateur qui permet de passer de l'hypoténuse au côté opposé.
C'est un nombre inférieur à 1.
!
! = ! = ! = ! ou côté adjacent x ! = côté opposé
La tangente est le multiplicateur qui permet de passer du côté adjacent au côté opposé.
C'est un nombre qui peut être inférieur, ou égal, ou supérieur à 1
AB
AC
AB1
AC1
côté adjacent à A
!
hypoténuse
cosA
!
cosA
!
BC
AC
B1C1
AC
côté opposé à A
!
hypoténuse
sinA
!
sinA
!
BC
AB
B1C1
AC1
côté opposé à A
!
côté adjacent à A
!
tanA
!
tanA
!
A
C
B
C1
B1

2. Reconnaître les côtés dans un triangle quelconque.
!
A) Repérer les côtés par rapport à l’angle aigu choisi
!
!
!
!
!
!
!
!
B) Les formules
Cosinus, sinus et tan sont des coefficients de proportionnalité : !
hypoténuse côté adjacent
!
hypoténuse côté opposé
!
côté adjacent côté opposé
!
C) Pour trouver les angles
! = ! / ! = ! / ! = !
Pour mémoriser :
!
!
A
cosA
!
côté adjacent à A
!
hypoténuse
sinA
!
côté opposé à A
!
hypoténuse
tanA
!
côté opposé à A
!
côté adjacent à A
!
SOH
sin
!
CAH
cos
!
TOA
tan
!
x cos A
∧
: cos A
∧
x sin A
∧
: sin A
∧
x tan A
∧
: tan A
∧
A
B
C
côté adjacent
côté opposé à
hypoténuse
■
côté opposé à
côté adjacent à
hypoténuse
A
C
B
■

3. Savoir calculer un côté.
A) On connaît 2 côtés du triangle
Le triangle EFG est rectangle en E.
Appliquons le théorème de Pythagore
GF2 = EG2 + EF2
5,42 = EG2 + 52
29,16 = EG
2 + 25
EG
2 = 29,16 – 25
EG = ! (cm) valeur exacte
EG ≈ 2,0 (cm) arrondi au dixième
!
B) On connaît un côté et un angle
!
Exemple 1
Le triangle RST est rectangle en S. Utilisons la trigonométrie.
• Je cherche RS : côté adjacent à l'angle !. Je connais l'hypoténuse RT.
RS = RT x cos !
RS = 5,2 x cos 28°
RS ≈ 4,6 (cm)
!
• Je cherche TS : côté opposé à l'angle !. Je connais
l'hypoténuse RT.
TS = RT x sin !
TS = 5,2 x sin 28°
TS ≈ 2,4 (cm)
!
Exemple 2
Le triangle ABC est rectangle en B. Utilisons la trigonométrie.
• Je cherche AC : l'hypoténuse. Je connais le côté adjacent AB.
AC = !
AC = !
AC ≈ 5,9 (cm)
!
• Je cherche BC : le côté opposé. Je connais le côté adjacent AB.
BC = AB x tan !
BC = 5 x tan 32
BC ≈ 3,1 (cm)
!
4,16
R
!
R
!
R
!
R
!
AB
cos A
!
5
cos32°
A
!
4,75
AB
C
5 cm
32°
4,75 2,85
7,6
5,7
5,13
EF
G
5,4 cm
5 cm
5,7
RS
T
28°
5,2 cm
?
?

4. Savoir calculer un angle dans un triangle rectangle.
A) On connaît l’autre angle aigu
Le triangle RTS rectangle en R.
Propriété : Les angles aigus ! et ! sont complémentaires.
! = 90 – !
! = 90° – 28°
! = 62°
!
B) On connaît deux côtés
Exemple 1
Le triangle EGF est rectangle en E. Utilisons la trigonométrie.
Je connais [EF] : c'est le côté opposé.
Je connais [EG] : c'est le côté adjacent.
!
tan ! = !
tan ! = !
! = tan–1 ( ! )
! ≈ 59°
!
Exemple 2
Le triangle EGF est rectangle en E. Utilisons la trigonométrie.
Je connais [EF] : c'est le côté opposé.
Je connais [FG] : c'est l'hypoténuse.
!
sin ! = !
sin ! = !
! = sin–1 ( ! )
! ≈ 68°
!
!
!
ˆ
R
ˆ
T
ˆ
T
ˆ
R
ˆ
T
ˆ
T
G
!
EF
EG
ˆ
G
5
3
ˆ
G
5
3
ˆ
G
G
!
EF
EG
G
!
5
5, 4
ˆ
G
5
5, 4
ˆ
G
tan–1
on utilise la touche pour trouver l'angle.
sin–1
on utilise la touche pour trouver l'angle.
4,75 2,85
EF
G
5 cm
3 cm
?
5,7
RS
T
28°
?
?
4,75 2,85
7,6
5,7
5,13
EF
G
5,4 cm
5 cm

5. Trouver une démarche pour aboutir à un résultat
!
!
!
!
!
!
!
!
!
!
!
Démarche
L'augmentation est égale à EC – IC
• On calcule IC (dans le triangle rectangle IHC)
• On calcule EC (dans le triangle rectangle EHC)
— On calcule d'abord HC pour avoir une 2ème mesure dans le triangle EHC
— On calcule EC
• On calcule de combien on rallonge la laisse.
!
Rédaction
Etape 1 : Je calcule IC
Le triangle IHC est rectangle en H.
On cherche IC, l'hypoténuse et on connaît IH, le côté opposé à l'angle de 40°.
IC =!
IC = !
IC ≈ 9,3 (m)
!
Etape 2 : Je calcule HC
Je cherche HC qui est le côté adjacent à l'angle de 40°. Je connais le côté opposé IH.
HC = !
HC = !
HC ≈ 7,2 (m)
!
Etape 3 : Je calcule IC.
Le triangle CEH est rectangle en H.
Je cherche EC qui est l'hypoténuse. Je connais les deux autres côtés EH et CH.
Selon le théorème de Pythagore :
EC
2 = EH2 + HC2
EC2 = (3 + 6)2 + (!)2
IH
sin C
!
6
sin 40°
IH
tan C
!
6
tan 40°
6
tan 40°
Un propriétaire a un chien attaché au piquet planté en C.
La longueur initiale CI de la laisse permet au chien
d'atteindre le début du portail, au point I lorsque la laisse
est tendue.
Pour une meilleure surveillance de l'entrée, le propriétaire
aimerait que son chien puisse atteindre le portail à l'autre
bout soit au point E.
De quelle longueur minimale le propriétaire doit-il
rallonger la laisse de son chien ?