Comment tracer un triangle dont on connait les 3 longueurs - g

I. Le cercle
Définition :
Un cercle est formé de tous les points situés à la même distance d'un point appelé ………………………….
Cette distance est appelée le …………………… du cercle.
• les …………………………… [DO], [EO] et [OF] sont des …………………… du cercle
• le …………………… [GH] est appelé une ………………………
• le segment [EF] est appelé un ………………………….., qui mesure le …………………
d'un rayon
• la portion de cercle en rouge est appelée un …… …… …………………, noté ……………
II. Les polygones
Définition :
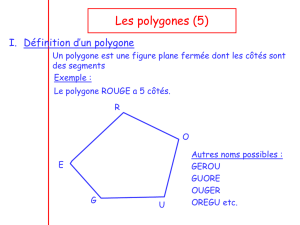
Un polygone est une figure ………………… dont les côtés sont des …………………….
Les points A, B et C … sont des …………………………… du polygone.
Les segments [AB], [BC] et [CD] … sont les ………………………………………………………….
Les segments [AC], [AE] … sont des ………………………………… du polygone.
Pour nommer un polygone, il faut lire les sommets en "……………………." autour du quadrilatère.
On peut donc appeler le polygone …………………………………………………………………mais pas …………………………………………………
1. Cas particulier : les triangles
Définition :
Un ………………………… est un polygone à ………………… côtés.
Comment tracer un triangle dont on connait les 3 longueurs ?
On commence généralement par tracer le plus …………………………… côté.
Avant de commencer un tracé, il est vivement conseillé de faire un croquis à main levé.
Chapitre 4 :
Figures usuelles

Définition :
Un triangle ………………………… est un triangle qui a deux côtés de même longueur.
Exemple :
 Le triangle DSP est un triangle …………………………… en ……….
 Le segment [SP] est appelé la ………………………………… du triangle isocèle.
Propriété :
Dans un triangle isocèle, les angles à la base ont ………………………………………………………………………………………
Définition :
Un triangle ……………………………… est un triangle qui a …… côtés de même longueur.
Exemple :
Le triangle UTF est un triangle …………………………………
Le triangle UTF est également …………………………… en T, en U et en F.
Propriété :
Dans un triangle équilatéral, les trois angles ……………………………………………………………………………………….
Définition :
Un triangle …………………………………… est un triangle qui a un
angle …………………………….
On appelle …………………………………… le côté opposé à l'angle droit.
Le triangle REM est un triangle ……………………en ……. Le segment [RE] s’appelle l’……………………………… du triangle.
Un triangle rectangle isocèle est un triangle qui est à la fois ……………………………………… et …………………………….
Tracé d’un triangle rectangle connaissant les deux côtés de l’angle droit :
Tracé d’un triangle rectangle connaissant un côté de l’angle droit et l’hypoténuse :

2. Cas particulier : les quadrilatères
Définition :
Un ………………………………………………… est un polygone
à ………………… côtés.
LE RECTANGLE
Définition :
Un …………………………………… est un quadrilatère qui a ……… angles droits.
Voici une méthode de construction pour tracer un rectangle ABCD tel que AB = 5 cm et BC = 3 cm.
Propriété :
Un rectangle a ses côtés opposés ………………………………… et de même ………………………….
De plus, ses diagonales ont la même …………………………………… et se coupent en leur …………………………….
LE LOSANGE
Définition :
Un ……………………………… est un quadrilatère qui a ………… côtés égaux.
Voici une méthode de construction pour tracer un losange ABCD tel que AB = 5 cm et AC = 4 cm.
On trace un segment [AB] de longueur 5 cm.
On trace un arc de cercle de centre B et de rayon 5 cm
et un arc de cercle de centre A et de rayon 4 cm.
On trace le point D qui est également à 5 cm du point A et du point C.
A l’aide du compas, on trace un arc de cercle de centre A puis de C de
rayon 5 cm.

Propriété :
Un losange a ses côtés opposés ………………………………….
De plus, ses diagonales sont …………………………………………………… et qui se coupent en leur ………………………….
LE CARRE
Définition :
Un …………………………… est un quadrilatère qui a 4 …………………… ………………………
et 4 ………………………… ………………………… .
Un carré est donc à la fois un …………………………… et un …………………………….
Voici une méthode de construction pour tracer un carré ABCD tel que AB = 4 cm.
Propriété :
Un carré a ses côtés opposés …………………………………. De plus, ses diagonales sont ……………………………………,
se coupent en leur …………………… et ont la même …………………………………….
AUTRES QUADRILATERES
Définition :
Un ………………………………………………… est un quadrilatère qui a deux paires
de côtés consécutifs ……………….
Ses diagonales sont …………………………………………………
Définition :
Un …………………………………………….. est un quadrilatère qui a ses côtés
opposés ……………………………………….
Définition :
Un ………………………………… est un quadrilatère qui a deux côtés
………………………………………. Ces deux côtés sont appelés « …………… du
trapèze », la grande ……………. et la petite ……………..