MP*1-2016/2017 DM5 facultatif Purification par décantation en bassin X-MP-2001-Extrait

1
MP*1-2016/2017
DM5 facultatif
X-MP-2001-Extrait
Purification par décantation en bassin
Constantes physiques :
Charge élémentaire  
Constante de Bolzmann  
Nombre d’Avogadro 
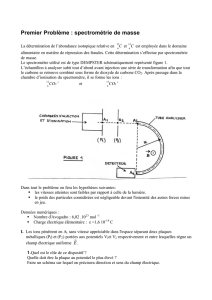
1-a) Représenter l’orientation du champ électrique   en justifiant votre réponse.
1-b) Quelle est la relation liant le potentiel  et la charge volumique  dans la
solution ?
1-c) La solution contient des ions positifs et négatifs de charges  et . On suppose que
le nombre volumique d’ions de charge   est 
 et le nombre
volumique d’ions de charge    est  
 ;  est la constante de
Bolzmann et T la température de la solution. Montrer que la charge volumique s’exprime par
. En déduire l’équation différentielle vérifiée par le potentiel 
2-a) On appelle  le potentiel à la surface de la particule, considérée comme le plan    et
on pose . Estimer un ordre de grandeur de 
 pour une eau à  et  . A
l’aide d’une argumentation judicieuse, commenter l’ordre de grandeur du résultat obtenu.

2
On se placera dans la suite du problème dans le cas 
  .
2-b) Simplifier puis résoudre l’équation différentielle vérifiée par 
On posera  
. Comment interpréter physiquement cette quantité ?
2-c) Le champ électrique 
 dans la solution au voisinage de la surface dépend de la densité
surfacique de charges  sur la surface et de . On prendra 
. Relier  à  et montrer
que cette relation est la même que pour un condensateur plan dont on précisera l’épaisseur.
2-d) Calculer  à la température de  pour une solution d’ions monovalents de
concentrations . Conclure sur la modélisation plane proposée par l’énoncé pour
des particules de  de rayon.
3-a) On peut, toujours dans la modélisation plane mais sans supposer 
 , calculer
l’énergie potentielle par unité de surface entre d’une particule dans le champ d’une autre
particule distante de l ; elle est donnée, après calculs, par : l 
 l  avec  
.
Donner la dimension de  et interpréter physiquement sa dépendance en l.
3-b) Les deux particules interagissent aussi par l’intermédiaire de la force de Van der Waals.
L’énergie potentielle correspondante par unité de surface entre les colloïdes est donnée par
l 
l où A est une constante positive. Il s’agit d’étudier les variations de l’énergie
potentielle totale entre deux colloïdes : lll.
A quelle condition sur  existe-t-il des extrema de l ? On précise que la fonction
 présente un maximum pour    avec     .
3-c) Déterminer la plus petite valeur  pour laquelle la valeur du maximum est nulle.
3-d) On suppose que le colloïde est stable pour  . On définit  la valeur
critique de  pour laquelle la valeur du maximum est nulle. En utilisant l’expression de 
donnée par l’énoncé, indiquer pour quelles valeurs de  le colloïde est stable ou instable.
3-e) Dire simplement pourquoi l’eau de mer est limpide.