Chap 8

Sirius Term S - Livre du professeur
Chapitre 8. Principe d’inertie et quantité de mouvement
© Nathan 2012 8 / 17
Exercices d’application
5 minutes chrono !
1. Mots manquants
a. le solide de référence
b. repère de temps
c. horloge
d. la dérivée ; position
e. le vecteur vitesse
f. immobile ; uniforme
g. son vecteur vitesse
h. système isolé
i. référentiel galiléen
2. QCM
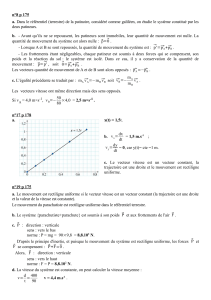
a. La première représentation (ci-contre) est la représentation de x(t) pour un point
en mouvement rectiligne uniforme est une droite :
x(t) = vxt + x0
La deuxième représentation (x(t) = constante) correspond à un point immobile.
La troisième représentation correspond à un point dont la vitesse n’est pas constante.
b. Le passager est en mouvement rectiligne uniforme dans le référentiel terrestre
alors qu’il est immobile dans le référentiel du train.
c. p = mv, la masse étant en kg et la vitesse en ms-1.
36
0,100 3,6 p
=1,0 kgms-1.
-----------------------------------------------------------------------------------------------------------------
Compétences exigibles
3. Un objet tombe dans un train en mouvement.
Dans le référentiel du train, la trajectoire de son centre d’inertie est une droite verticale.
Dans le référentiel terrestre, la trajectoire est une courbe, combinaison du mouvement de
chute et du mouvement du train.
-----------------------------------------------------------------------------------------------------------------
4. a. À t0 = 0 s, x(t0) = 1 et y(t0) = 3.
Le vecteur position est par définition : (t0) = x(t0) + y(t0) .
b. Le vecteur vitesse est la dérivée du vecteur position par rapport au temps :
et = = 5 ms-1 ; = = 0
c. Le vecteur vitesse est un vecteur constant, la trajectoire est une droite et le mouvement est
rectiligne uniforme.
----------------------------------------------------------------------------------------------------------------
5. a. Le vecteur vitesse est la dérivée du vecteur position par rapport au temps.
b. L’expression approchée du vecteur vitesse étant :
Le vecteur vitesse à la date t3 a même direction et même sens que le vecteur .
Sa valeur est donnée par :
4
32.
2
AA
v

Sirius Term S - Livre du professeur
Chapitre 8. Principe d’inertie et quantité de mouvement
© Nathan 2012 9 / 17
Pour tout le quadrillage : 13 carreaux représentent 13 cm dans la réalité et mesurent 7,0 cm
sur le papier, A2A4 représentent x cm dans la réalité et mesure 2,4 cm sur le papier ; la règle de
proportionnalité permet écrire :
2,4 13 2,4 4,5 cm
13 7,0 7,0
xx
2-1
33
4,5 10 0,56 m s
2 40 10
v
-----------------------------------------------------------------------------------------------------------------
6. a. Le tracé correspondant au centre d’inertie du mobile est celui du traceur « B ».
b. Le tracé correspondant au centre d’inertie est formé de points alignés et régulièrement
répartis : le mouvement du centre d’inertie est rectiligne
uniforme. D’après le principe d’inertie, le système étudié
dans un référentiel considéré comme galiléen est alors un
système isolé si : = alors .
c. Le mobile autoporteur est en interaction avec la Terre, le
coussin d’air et l’air ambiant d’où le diagramme suivant :
L’action due à la Terre est modélisée par le poids , l’action
du coussin d’air par une force . En négligeant l’action de
l’air ambiant : + = soit = - .
-----------------------------------------------------------------------------------------------------------------
7. a. Le vecteur quantité de mouvement d’un point matériel de masse m et animé d’une
vitesse
v
est :
.p mv
Le vecteur quantité de mouvement d’un système matériel est égale à la somme des vecteurs
quantités de mouvement des n points matériels qui le constituent : = .
b. p = mv = 1,0 × 103 ×
120
3,6
= 3,3 × 104 kgms-1.
c. On note M, la masse du camion et V, sa vitesse.
p = mv = MV ; d’où V =
mv
M
. A.N. : V =
1120
30
= 4,0 kmh-1.
----------------------------------------------------------------------------------------------------------------
8. a. Dans le référentiel terrestre considéré comme galiléen, on étudie le système constitué par
les deux patineurs.
b. Avant qu’ils ne se repoussent, les patineurs sont immobiles, leur quantité de mouvement est
nulle. La quantité de mouvement du système est alors nulle : = .
Lorsque A et B se sont repoussés, la quantité de mouvement du système est : .
Les frottements étant négligeables, chaque patineur est soumis à deux forces qui se
compensent, son poids et la réaction du sol : le système étudié est isolé.
Dans ce cas, il y a conservation de la quantité de mouvement : = .
Les vecteurs quantité de mouvement de A et de B sont opposés : .
c. L’égalité précédente se traduit par :
(t) = - (t) soit (t)
Les vecteurs vitesse ont même direction mais des sens opposés.
Si vA = 4,0 ms-1, vB =
A
B
m
m
vA =
50
80
× 4,0 = 2,5 ms-1.
-----------------------------------------------------------------------------------------------------------------

Sirius Term S - Livre du professeur
Chapitre 8. Principe d’inertie et quantité de mouvement
© Nathan 2012 10 / 17
Compétences générales
9. On exprime la durée 32 millions d’années en seconde :
Δt = 32 millions d’années = 32 × 106 × 365 jours = 32 × 106 × 365 × 24 × 3600 = 1,0 × 1015 s.
Il y a le même rapport (1015) entre une femtoseconde et une seconde, et entre une seconde et
32 millions d’années.
-----------------------------------------------------------------------------------------------------------------
10. a. R. Feynman décrit ses observations dans un référentiel lié au chariot.
b. Son père se place dans le référentiel terrestre.
c. Le système étudié est le ballon. Il est soumis à son poids et à la réaction du support, les
deux forces se compensent, il est donc isolé.
D’après le principe d’inertie, le centre d’inertie du ballon est soit immobile, soit en
mouvement rectiligne uniforme dans un référentiel galiléen :
- si le chariot et le ballon sont initialement immobiles, lorsque l’on tire le chariot, le
ballon garde sa position dans le référentiel terrestre, il « recule » dans le référentiel du
chariot qui n’est pas galiléen ;
- si le chariot est en mouvement rectiligne uniforme, et qu’on l’arrête brusquement, le
ballon persévère dans son mouvement rectiligne uniforme dans le référentiel terrestre
galiléen. Il se précipite vers l’avant dans le référentiel du chariot qui n’est pas galiléen.
-----------------------------------------------------------------------------------------------------------------
11. La masse du gros poisson est notée M, celle du petit poisson m.
On étudie la quantité du mouvement du système constitué par les deux poissons « avant » puis
« après » que le gros poisson est avalé le petit.
Le système étant supposé isolé, la conservation de la quantité de mouvement donne :
’
kmh-1
-----------------------------------------------------------------------------------------------------------------
12. a. Les trajectoires sont des droites. Les points sont régulièrement répartis : les vitesses sont
constantes. A et B sont donc en mouvement rectiligne uniforme.
b. La vitesse est v =
dt
, d étant la distance parcourue pendant un intervalle de temps Δt.
La distance parcourue par B est plus grande que la distance parcourue par A pendant le même
intervalle de temps Δt donc : vB > vA.
B est le mobile qui a acquis la plus grande vitesse.
c. Les quantités de mouvement étant égales, pA = pB soit mAvA = mB vB.
Si vB > vA, mB < mA.
A est le mobile le plus lourd.
-----------------------------------------------------------------------------------------------------------------

Sirius Term S - Livre du professeur
Chapitre 8. Principe d’inertie et quantité de mouvement
© Nathan 2012 11 / 17
Exercices de méthode
13. Exercice résolu.
-----------------------------------------------------------------------------------------------------------------
14. a. Le mouvement est rectiligne uniforme :
cte.
G
v
b. D’après le principe d’inertie, le référentiel terrestre étant considéré galiléen, si
cte
G
v
alors = .
Le système étudié est alors isolé.
c. Le skieur est en interaction avec la Terre, le sol et l’air.
Il subit trois actions modélisées respectivement par le poids , la réaction et la force de
frottement .
d.
e. D’après le principe d’inertie : + .
Suivant l’axe x’x parallèle à la pente et l’axe y’y normal à la pente :
Px + Rx + fx = 0 P sin α + 0 – f = 0
Py + Ry + fy = 0 - P cos α + R + 0 = 0
La force est telle que = -f de valeur f = P sin α.
A.N. : f = 70 × 9,8 × sin 20° = 2,3 × 102 N.
----------------------------------------------------------------------------------------------------------------
15. a. Par rapport au référentiel terrestre, l’échelle est en mouvement rectiligne uniforme.
Par rapport au référentiel du camion, l’échelle est immobile.
b. L’échelle est le système étudiée : elle est soumise à son poids et à la réaction du support.
Dans le référentiel terrestre considéré galiléen, elle est en mouvement rectiligne uniforme.
D’après le principe d’inertie, elle constitue un système isolé : les deux forces se compensent.
Le raisonnement peut être effectué dans le référentiel du camion qui est aussi galiléen quand
le camion est en mouvement rectiligne uniforme.
c. Lorsque le camion freine, l’étude du système est identique à celle réalisée dans la
question b. dans le référentiel terrestre : l’échelle persévère dans son mouvement et se déplace
donc vers l’avant du camion qui ralentit. Par contre, le référentiel du camion n’est plus
galiléen et le principe d’inertie ne s’applique plus
d. Dans le référentiel terrestre, l’échelle est toujours le système étudié. Elle n’est soumise qu’à
son poids. Le principe d’inertie ne s’applique pas car elle ne constitue pas un système isolé.
Son centre d’inertie ne peut pas être en mouvement rectiligne uniforme.
-----------------------------------------------------------------------------------------------------------------

Sirius Term S - Livre du professeur
Chapitre 8. Principe d’inertie et quantité de mouvement
© Nathan 2012 12 / 17
Exercices d’entraînement
16. a. L’enregistrement du mouvement de A donne des points alignés et équidistants : le
mouvement est rectiligne et uniforme. La vitesse de A est calculée non pas sur un mais sur
quatre intervalles de temps pour une plus grande précision :
vA =
2
2
2,2 10 3
4 2,0 10
= 0,83 ms-1
On détermine de même la vitesse de B :
vB =
2
2
1,6 10 3
4 2,0 10
= 0,60 ms-1
Les trajectoires de A et de B sont colinéaires, les vecteurs vitesse de A et de B ont donc même
direction mais des sens opposés.
b. Le vecteur quantité de mouvement de A est par définition
p
A=
AA
mv
.
Il a même direction et même sens que le vecteur vitesse de A ; sa valeur est :
pA = mAvA = 0,720 × 0,83 = 0,60 kgms-1.
De même le vecteur quantité de mouvement de B est par définition :
p
B =
BB
mv
.
Il a même direction et même sens que le vecteur vitesse de B ; sa valeur est :
pB = mBvB = 0,980 × 0,60 = 0,59 kgms-1.
c. Les vecteurs quantité de mouvement ont même direction et des sens opposés comme les
vecteurs vitesse, leurs valeurs sont quasi égales :
AB
pp
.
La conservation de la quantité de mouvement avant et après l’explosion du système constitué
par les deux mobiles impose que
avant après.pp
Les mobiles avant l’explosion étant immobiles :
p
=
0
.
Après l’explosion, l’étude de l’enregistrement montre que :
p
A+
p
B =
0
.
On a bien
avant après.pp
-----------------------------------------------------------------------------------------------------------------
17. a. x(t) = 1,5t.
b.
x v
=
dx
dt
= 1,5 ms-1 ;
y
v
=
dy
dt
= 0.