Fonction exponentielle et encadrement du nombre e

Fonction exponentielle – Encadrement du nombre  – Exercices corrigés
© SOS DEVOIRS CORRIGES (marque déposée)
1
Sont abordés dans cette fiche : (cliquez sur l’exercice pour un accès direct)
 Exercice 1 : encadrement de  par deux fonctions
 Exercice 2 : encadrement de  obtenu par une fonction et des changements de variables
 Exercice 3 : encadrement de  par la somme de factorielles et écriture d’un algorithme
 Exercice 4 : valeur du nombre  en faisant appel à l’intégration (intégration par parties)
Fonction exponentielle – Encadrement du nombre 
Exercices corrigés

Fonction exponentielle – Encadrement du nombre  – Exercices corrigés
© SOS DEVOIRS CORRIGES (marque déposée)
2
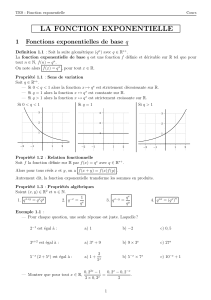
Pour tout , on pose 
 et .
1) Montrer que, pour tout ,  et .
2) En déduire un encadrement de .
1) Montrons que, pour tout ,  et .
a) Montrons tout d’abord que .
Rappel : Fonction exponentielle et inverse d’un réel
Pour tout , 
 avec .
La fonction  est définie par 
 , produit de deux fonctions continues et dérivables sur ,
d’une part la fonction  (fonction inverse de l’exponentielle) et la fonction 
(fonction polynôme de degré 2) d’autre part.
Par conséquent, il vient que la fonction  est dérivable sur  donc sur .
Rappel : Fonction exponentielle et dérivée
Soit  une fonction dérivable sur un intervalle . La fonction définie par  est dérivable sur  et, pour tout
, 
Remarque importante : Il en découle les résultats suivants : pour tout ,  et .
Ainsi, pour tout ,
Pour tout ,  et 
 donc .
Ainsi, pour tout , . La fonction  est donc décroissante sur .
Exercice 1 (2 questions) Niveau : facile
Correction de l’exercice 1  Retour au menu

Fonction exponentielle – Encadrement du nombre  – Exercices corrigés
© SOS DEVOIRS CORRIGES (marque déposée)
3
Par ailleurs, la fonction  étant continue en , 
existe et 
.
En conclusion, pour tout , .
b) Montrons désormais que .
La fonction  est définie par 
 , produit de deux fonctions continues et dérivables sur ,
d’une part la fonction  (fonction inverse de l’exponentielle) et la fonction 
(fonction polynôme de degré 2) d’autre part.
Par conséquent, il vient que la fonction  est dérivable sur  donc sur .
Ainsi, pour tout ,
D’une part, pour tout , . D’autre part, pour tout , . Enfin, pour tout ,
 (car la fonction  est décroissante sur ), d’où  (du fait de la croissance
de la fonction  sur ), c’est-à-dire . Il s’ensuit que, pour tout , . La
fonction  est donc croissante sur .
Par ailleurs, la fonction  étant continue en , 
existe et 
.
En conclusion, pour tout , .
2) Cherchons dès lors un encadrement de .
D’après la question précédente, pour tout ,  est décroissante, donc . Comme
 et comme, d’après la question précédente, , il vient que
.
On a également établi que, pour tout ,  est croissante, donc . La question
précédente a permis de montrer que . Par ailleurs, 
. Par conséquent,
.
Il résulte alors que 
. En multipliant par , il vient finalement que .
Remarque : Ce résultat est conforme à celui affiché par la calculatrice : .

Fonction exponentielle – Encadrement du nombre  – Exercices corrigés
© SOS DEVOIRS CORRIGES (marque déposée)
4
Soit la fonction  définie sur  par .
1) Montrer que, pour tout  réel, .
2) En déduire que, pour tout réel , 
.
Soit  un entier naturel tel que .
3) Démontrer que 
.
4) Démontrer que 
.
5) En déduire un encadrement de  en fonction de .
1) Montrons que, pour tout  réel, , c’est-à-dire montrons que .
La fonction  est la somme de deux fonctions continues et dérivables sur  : d’une part la fonction 
(fonction exponentielle) et d’autre part la fonction  (fonction affine).
Par conséquent, la fonction  est dérivable sur  et, pour tout , .
Rappel : Résolution d’inéquation de la forme 
Soient  et  deux fonctions définies sur un intervalle  (ou une réunion d’intervalles).
Pour tout réel ,  si et seulement si .
Or, . Ainsi, pour tout , , c’est-à-dire
 croissante sur , et pour tout , , c’est-à-dire  strictement décroissante sur .
Autrement dit,  admet un minimum, atteint en . Comme , pour tout ,
. Finalement, pour tout , , c’est-à-dire .
2) Montrons désormais que, pour tout réel , 
.
La question précédente a permis d’établir que, pour tout , . En remplaçant  par , il vient
alors l’inégalité .
Or, pour tout réel ,  car la fonction  est décroissante sur . Par conséquent, pour
tout réel ,   
 car la fonction   est décroissante
sur 
 et car . En définitive, 
 pour tout réel .
Exercice 2 (5 questions) Niveau : moyen
Correction de l’exercice 2  Retour au menu

Fonction exponentielle – Encadrement du nombre  – Exercices corrigés
© SOS DEVOIRS CORRIGES (marque déposée)
5
3) Démontrons que 
, où 
Posons 
 et notons que  existe car .
Pour tout  , d’où 
, c’est-à-dire  .
D’après la question 1), pour tout , . Il vient alors que 
. D’où 
(car la fonction  est croissante pour tout  et tout ). Finalement, pour tout  entier naturel tel
que , 
.
4) Démontrons que 
.
Posons  
 et notons que  existe car .
Pour tout  , d’où  et 
 (d’après la décroissance de la fonction 
 sur 
),
c’est-à-dire 
.
D’après la question 2), pour tout , 
. Il vient alors que 
.
Or, 
. Finalement, pour tout  entier naturel tel
que , 
.
5) Des deux questions précédentes, on conclut que 
.
Remarque : Plus  est grand, plus l’encadrement de  est précis. Si , alors . Si
 ,  (encadrement à  près).
Remarque : est l’intervalle des
entiers naturels supérieurs ou égaux à 2.
En fait, .
Pour tout réel  et pour tout entier relatif
, . Par ailleurs, .