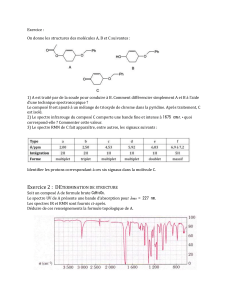
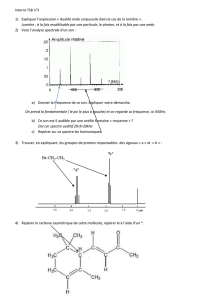
TD d`Analyse Spectrale 1 Calcul fonctionnel continu 2 Spectre 3

FIMFA, Mai 2006
Rachel Ollivier
TD d’Analyse Spectrale
-III-
1 Calcul fonctionnel continu
Soient Aune C∗-algèbre et a∈A.
1. Montrer que pour toute fonction fcontinue sur Sp a∗a∪ {0}, on a af(a∗a) = f(aa∗)a.
2. On suppose que aest hermitien. Montrer qu’il existe un unique élément hermitien bde
Atel que b3=a.
2 Spectre
1. Un élément d’une C∗-algèbre de spectre contenu dans R+est-il toujours positif ?
2. Soit Hun espace de Hilbert. Caractériser par leur spectre les éléments hermitiens de
L(H)qui sont des projecteurs.
3. Soient Hun espace de Hilbert, T∈ L(H)un opérateur normal et λun point isolé du
spectre de T. Montrer que λappartient au spectre ponctuel de T
3 Idempotent dans une C∗-algèbre
Soit Aune algèbre de Banach unifère complexe. On suppose qu’elle contient un idempotent p
de norme 1. On lui associe les ensembles
Cp={a∈A, ap =pa}, Ap={a∈A, ap =pa =a}.
1. Vérifier que Appeut-être considérée comme une algèbre de Banach unitaire dont l’unité
est p.
2. On pose q= 1 −pet l’on suppose que qest de norme 1. Soit a∈Cp, on définit ap=pa,
aq=qa. Ce sont des éléments respectifs de Apet Aq. Montrer que le spectre de aest la
réunion du spectre de apdans Apet du spectre de aqdans Aq.
3. On suppose que Aest une C∗-algèbre et que a∈Aest un élément normal dont le spectre
est égal à la réunion de deux compacts disjoints non-vides Pet Qdu plan complexe.
On désigne par p=1P(a)l’image de la fonction indicatrice 1Ppar le calcul fonctionnel
continu associé à a. Montrer que le spectre de apest P, celui de aqest Q. Montrer que
le calcul fonctionnel associé à apest donné par
Φap(f) = ˜ f(a)p,
où ˜ fest un prolongement de f∈C(Sp ap)en une fonction continue sur le spectre de a.
1

4 Mesure spectrale d’un opérateur unitaire
Soient Hun espace hilbertien complexe, U∈ L(H)une application linéaire continue inversible,
et e∈H. Pour tout n∈Z, on pose en=Un(e). On suppose que (en)n∈Zest une base
hilbertienne de H.
1. Déterminer le spectre résiduel et le spectre ponctuel de U.
2. Soit λun nombre complexe de module 1. Soit Vλl’opérateur unitaire défini par Vλ(en) =
λnenpour tout n∈Z.
(a) Montrer que si µ∈Sp(U)alors λµ ∈Sp(U).
(b) Déterminer le spectre de U.
(c) Déterminer la mesure spectrale de U.
5 Morphismes de C∗-algèbres
Soient Aet Bdes C∗-algèbres et π:A→Bun morphisme involutif. On note respectivement
A+et B+l’ensemble de leurs éléments positifs.
1. Montrer que πcommute avec le calcul fonctionnel : pour x∈Anormal, fcontinue sur
Sp(x), on a π(f(x)) = f(π(x)).Montrer ensuite que pour tout x∈A,π(|x|) = |π(x)|.
2. Montrer que xest un élément positif de Asi et seulement si x=|x|.
3. Montrer que l’on a π(A+) = π(A)∩B+.
6 Monotonie du calcul fonctionnel
Soit Aune C∗-algèbre.
1. Montrer que si a, b ∈A+et a≤balors kak ≤ kbk.
2. Soient a, b, x ∈Atels que a≤b. Montrer que x∗ax ≤x∗bx.
3. Pour tout a, b ∈A, montrer que a∗b∗ba ≤ kbk2a∗a.
4. Soient a, b, x ∈A. Si a∗a≤b∗bmontrer que kaxk ≤ kbxk.
5. Supposons Aunifère. Soient a, b ∈Aet supposons binversible. Alors les propriétés
a∗a≤b∗bet kab−1k ≤ 1sont équivalentes.
6. Supposons Aunifère. Soient a, b ∈A+deux éléments inversibles. Alors les propriétés
a≤bet b−1≤a−1sont équivalentes.
7 A propos du spectre de l’algèbre des fonctions continues sur
un compact
Cet exercice montre que les fonctions continues sur un compact séparent les points. Un espace
topologique Xest dit normal si pour toute paire Aet Bde fermés disjoints de Xil existe des
ouverts disjoints Uet Vde Xtels que A⊂Uet B⊂V.
a) Montrer que tout espace métrique est normal.
b) Démontrer que tout espace compact est normal.
Soit Xun espace topologique.
2

c) Montrer que Xest normal si et seulement si, pour toute partie fermée Fet toute partie
ouverte Vde Xtelles que F⊂V, il existe une partie ouverte Ude Xtelle que F⊂U
et U⊂V.
Soit X un espace topologique normal Fune partie fermée et Vune partie ouverte de X
telles que F⊂V.
d) Montrer qu’il existe une famille Urd’ouverts de Xindexée par Q∩]0,1[ telle que pour
tout couple r, s d’éléments de Q∩]0,1[ tels que r < s on ait F⊂Ur⊂Ur⊂Us⊂Us⊂
V.
e) En déduire qu’il existe une application continue f:X→[0,1] nulle sur Fet égale à 1
hors de V.
3