Correction des exercices Ex 6 p 38 Spectre 1 : spectre de raie, d

Correction des exercices
Ex 6 p 38
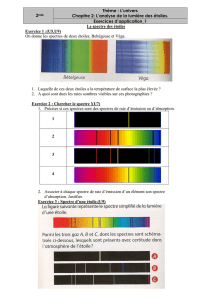
Spectre 1 : spectre de raie, d'émission.
Spectre 2 : Spectre de raie, d'absorption.
Spectre 3. Spectre continu, d'émission.
Relire si problème le 3. p32
Ex 10 p 38
1. a.
Spectre 1 : spectre de raie, d'émission.
Spectre 2 : Spectre de raie, d'absorption.
b. Ces deux spectres correspondent à la même entité chimique car les raies sont situées aux mêmes
endroits : dans un cas il y a émission de lumière (spectre 1), dans l'autre cas la lumière est absorbée.
Relire si problème le 3. p32
2. Pour réaliser le spectre 1 d'émission le montage optique à faire est représenté doc 7 p 32 .
Pour réaliser le spectre 2 d'absorption le montage optique à faire est représenté doc 9 p 32 .
Ex 11 p 38
L'exercice sera corrigé en prenant le niveau 1 de réflexion.
1. a. En utilisant le document 1 p 31
501 nm : couleur verte
587 nm : couleur orangé
668 nm : couleur rouge
b. Le spectre B ne peut pas être celui de l'hélium car il ne possède pas de raie dans le rouge.
c. Le spectre C comporte les couleurs vert, orangé et rouge (plutôt rouge-violet).
2. a L'œil peut déceler des longueurs d'ondes comprises entre 400nm et 800nm.
b. Non car 300 nm < 400 nm, c'est donc invisible.
c. Il s'agit des UV
Ex 14 p39
1. Pour commencer on rentre les valeurs en colonne dans le logiciel Excel (ou l'équivalent dans
la suite open office).
On constate que les points ne sont pas alignés sur une droite qui passe par l'origine donc la
longueur d'onde et la température ne sont pas proportionnelles.
Température en fonction de longueur d'onde
0
500
1000
1500
2000
2500
3000
3500
0 500 1000 1500 2000 2500
Longueur d'onde (nm)
Température (°C)

2. Voici le résultat obtenu :
La dernière colonne doit se calculer automatiquement (à ne pas faire à la calculette) : avec
excel c'est plus simple et rapide. Il suffit de rentrer le calcul pour un cellule, par exemple
C2=1/A2, puis de faire glisser le carré qui apparaît en bas à droite de la cellule.
Voici le graphique obtenu :
3. L'équation de la droite (pour l'obtenir : clic droit sur la courbe, puis « ajouter une courbe de
tendance », puis « afficher l'équation sur le graphique ») est :
y= 2,88 E+06 x – 2,677 E+02
E+06 signifie 106 de même E+02 signifie 102 . Sur le graphique y est en ordonnée, il
représente la température θ et x est en abscisse, il représente
1/
.
On a donc :
=2,884 . 1061
−267,7
soit un résultat très proche de celui recherché.
4. Si on arrive à déterminer la longueur d'onde ou l'émission de l'étoile est maximale, alors on
peut en déduire sa température par la loi de Wien.