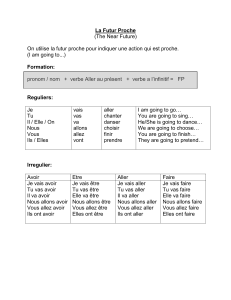
10:00-10:30 Jean-Philippe Bouchaud Une approche instanton pour les intégrales de Harish-Chandra-Itzykson-Zuber dans la limite de grand N

Cleaning correlation matrices,
HCIZ integrals &
Instantons
J.P Bouchaud
with: M. Potters, L. Laloux, R. Allez, J. Bun, S. Majumdar
Thank you Alain for having taught me so much!

Empirical Correlation Matrices
•Empirical Equal-Time Correlation Matrix E
Eij =1
TX
t
Xt
iXt
j
σiσj
Order N2quantities estimated with NT datapoints.
When T < N,Eis not even invertible.
Typically: N= 500 −2000; T= 500 −2500 days (10 years)
−→ q:= N/T =O(1)
•In many application (e.g. portfolio optimisation) one needs
to invert the correlation matrix – dangerous!
•How should one estimate/clean correlation matrices?

Rotational invariance hypothesis (RIH)
•In the absence of any cogent prior on the eigenvectors, one
can assume that Cis a member of a Rotationally Invariant
Ensemble – “RIH”
•In finance: surely not true for the “market mode”
~v1≈(1,1,...,1)/√N, with λ1≈Nρ, but OK in the bulk
•“Cleaning” Ewithin RIH: keep the eigenvectors, play with
eigenvalues
→The simplest, classical scheme, shrinkage:
C= (1 −α)E+αI→b λC= (1 −α)λE+α, α ∈[0,1]

RMT: from ρC(λ) to ρE(λ)
•Solution using different techniques (replicas, diagrams, free
matrices) gives the resolvent GE(z) = N−1Tr(E−zI) as:
GE(z) = Zdλ ρC(λ)1
z−λ(1 −q+qzGE(z)),
•Example 1: C=I(null hypothesis) →Marcenko-Pastur [67]
ρE(λ) = q(λ+−λ)(λ−λ−)
2πqλ , λ ∈[(1 −√q)2,(1 + √q)2]
•Suggests a second cleaning scheme (Eigenvalue clipping, [Laloux
et al. 1997]): any eigenvalue beyond the Marcenko-Pastur
edge can be trusted, the rest is noise.

Eigenvalue clipping
λ < λ+are replaced by a unique one, so as to preserve TrC=N.