rattrapage

S4 SMR 1er septembre 2005
EXAMEN DE THERMODYNAMIQUE
Dur´ee : 1 heure 30 mn
Les documents et les t´el´ephones portables ne sont pas autoris´es. Les calculatrices sont autoris´ees.
Bar`eme approximatif : Premier probl`eme 6 points ; deuxi`eme probl`eme 14 points.
Les deux probl`emes sont ind´ependants.
1 Hydrostatique.
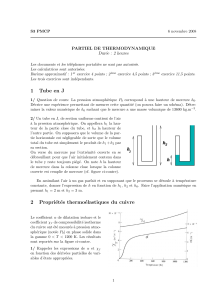
On renverse un verre cylindrique (section
S= 2 ×10−3m2, hauteur h0= 10 cm,
masse n´egligeable) au dessus d’une bas-
sine remplie d’eau, de sorte que le bord du
verre affleure la surface de l’eau (cf. figure
ci-contre, position (a)).
Ensuite, on pose sur le verre une masse
m= 100 g et on se retrouve dans la situa-
tion illustr´ee dans le cas (b) de la figure :
hest la distance entre le fond du verre et
l’interface air/eau `a l’int´erieur du verre et
xest la distance entre cette interface et la
surface libre de l’eau.
(b)
(a)
m
h
0
h
x
On notera ρla masse volumique de l’eau et P0la pression atmosph´erique.
1/ Calculer la valeur de xet de la pression Pde l’air pi´eg´e dans le verre en fonction des
param`etres du probl`eme. Faire l’application num´erique.
2/ On consid`ere l’air comme un gaz parfait. Donner l’expression de hen fonction de h0,m,
g,Set P0. Faire l’application num´erique. Peut-on avoir x > h ? Si oui, tracer la figure
correspondante.
Veuillez tourner la page, SVP
1

2 D´etente irr´eversible.
Dans cet exercice on se propose d’´etudier la varia-
tion d’entropie qui intervient lors d’une transforma-
tion irr´eversible d’un gaz. Le dispositif exp´erimental
est sch´ematis´e sur la figure ci-contre : un cyclindre
est ferm´e par un piston (Π) mobile sans frottements.
Une cloison fixe (F) d´elimite deux compartiments
dans le cylindre. Les parois du cylindre et le piston
sont adiabatiques. La face externe du piston est
soumise `a la pression atmosph´erique P0.
initial
final
(Π)
(Π)
(F)
(F)
V
V V
V P
P
0
02
1
0
0
Initialement, le compartiment limit´e par le piston est rempli d’un gaz parfait dont le capacit´e
thermique `a volume constant CVest ind´ependante de la temp´erature (on note γ=CP/CV). La
temp´erature est T1, le volume V1. L’autre compartiment, de volume V0est vide.
Pour op´erer la d´etente irr´eversible du gaz, on perce un trou dans la cloison fixe (F). Les
conditions intiales sont telles qu’une fois l’´etat d’´equilibre final est atteint, le piston d´elimite un
volume V2entre sa face interne et la cloison (F). Dans l’´etat final, la temp´erature du gaz est T2.
1/ Quelle est la pression du gaz dans l’´etat initial et dans l’´etat final ?
2/ Quel est le volume balay´e par le piston dans son d´eplacement de sa position initiale `a sa
position finale ? En d´eduire le travail Wfourni au gaz par le piston en fonction de V1,V2et P0.
3/ Donner, en la justifiant, l’expression de la diff´erentielle dU de l’´energie interne du gaz en
fonction de la variation dT de la temp´erature, du nombre nde moles ainsi que des constantes γ
et R.
Pour le gaz consid´er´e, calculer la variation de l’´energie interne en fonction des param`etres
de l’´etat initial et de l’´etat final (V0,V1,V2et P0).
4/ Calculer le volume V2et la temp´erature finale T2en fonction de V0,V1,T1et γ. La
temp´erature finale est-elle sup´erieure ou inf´erieure `a la temp´erature initiale ? Faire l’application
num´erique en prenant V0=V1= 1 `,T1= 300 K et γ= 1,4.
Quelle condition V0et V1doivent-ils remplir pour que le piston ne soit pas appliqu´e contre
la cloison fixe dans l’´etat final ?
5/ ´ Ecrire l’identit´e thermodynamique pour un syst`eme `a deux variables ind´ependantes (´energie
et volume). Pour nmoles de gaz parfait, en d´eduire la diff´erence d’entropie entre deux ´etats
(V1, T1) et (V2, T2). Calculer alors la variation d’entropie ∆Sdu gaz de l’exp´erience pr´ec´edente
en fonction de V0,V1,T1et γ. Quel doit ˆetre le signe de ∆S? V´erifier le dans le cas o`u V0=V1.
2