UMBB STH Faculté des sciences

UMBB STH
Faculté des sciences 2010/2011
Département de Physique
Physique2
ETLD 2
Exercice 1 :
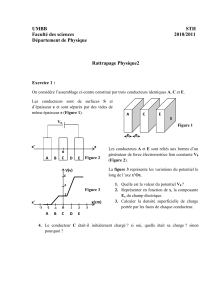
Trois charges ponctuelles   sont placées aux points A, B et D sommets d’un carré
ABCD de coté  comme l’indique la figure 1.
Déterminer :
1. le vecteur champ électrique au point C dû aux trois charges  . Représenter
graphiquement ce champ électrique.
2. le potentiel électrique au point C dû aux trois charges  .
3. le travail nécessaire pour déplacer une charge   de l’infini au point C. Quelle
est alors l’énergie potentielle de la charge  et la force électrique à laquelle est
soumise au point C.
4. l’énergie interne du système des quatre charges   . que représente cette
énergie.
5.
On donne :
          .
Exercice 2 :
1. Déterminer, en utilisant le théorème de Gauss, l’expression du champ électrique
)(rE
crée par une sphère de rayon R uniformément chargée en surface avec une densité σ.
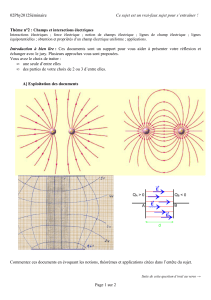
2. Deux sphères S1 et S2, concentriques, creuses, d’épaisseurs négligeables et de rayons
respectifs R1 et R2, sont chargées uniformément en surface avec des densités
respectives (+4σ) et (-σ).
i) Calculer la charge Q1 et Q2 portée par chacune des deux sphères.
ii) En déduire le champ électrique
)(rE
dans les régions : A(
1
Rr 
), B(
21 RrR 
) et
C(
2
Rr 
).
R1
R2
-σ
r
+4σ
O
S2
S1
A
B
C
M

3. Soit un point M situé à 15cm du centre O des deux sphères. Le potentiel électrique
crée en M par ces deux sphères est de 12 Volts.
i) Déterminer les expressions du potentiel électrique dans les régions A, B et C.
ii) Quelle est la forme des surfaces équipotentielles dans les régions A, B et C.
iii) En déduire les positions r1 et r2 des équipotentielles V1=24 Volts et V2=6 Volts.
Conclusion.
AN:
-8 -2
21
R =2 R =20 cm; =10 /4 Cm .
Exercice 3 :
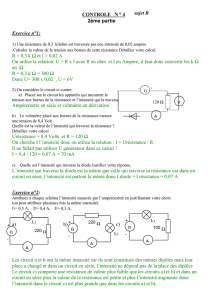
Soit le circuit électrique de la figure ci-dessous. On donne : E1=7V, E2=10V, R1=10Ω,
R2=15Ω, R3=21Ω, R4=15Ω, R5=10Ω et r1= r2=1Ω.
1. Trouver la résistance équivalente RAB entre les points A et B.
2. Calculer les courants qui traversent R1, R2 et RAB. En déduire les courants qui
traversent R4 et R5.
3. Calculer la tension VAB aux bornes de RAB.
4. Quelle est l’énergie dissipée par effet joule dans ce circuit durant 10 minutes de
fonctionnement.
R1
R2
R3
R4
R5
r1
r2
E1
E2
A
B

UMBB STH
Faculté des sciences 2010/2011
Département de Physique
Corrigé Physique2
ETLD 2
Exercice 1 (6 points): choix d’un système d’axes 
Solution : choix d’un système d’axes 
1. Vecteur champ électrique au point C dû aux trois charges:
2. potentiel dû aux trois charges au point C :
0.5
0.25
0.25
0.25
0.25
0.5
0.5

3. le travail nécessaire pour déplacer une charge  de l’infini au point C :
Le travail calculé ici est le travail d’une force extérieure « conservative » qui ne dépend que
de l’état initial et l’état final : 
L’énergie potentielle de la charge  est 
Au point C la charge  est soumise à une force électrique :
4. L’énergie interne du système des quatre charges est :
avec : 
 ,
soit :
Elle représente l’énergie nécessaire (travail qu’on doit fournir) pour assembler les quatre
charges dans la configuration actuelle.
0.5
0.5
0.5
0.5
0.5
0.5
0.5

Exercice 2 (8 points):
1. l’expression du champ électrique
)(rE
crée par une sphère de rayon R uniformément
chargée en surface avec une densité σ.
() rr E r E U
Le flux à travers la surface :
.E dS
Suivant le théorème de gauss :
int
0
.er
Q
E dS
2
int
2
r
. ( ) ( )4
0
( )4 0 ( ) 0
er
Pour R
E dS E r dS E r r
Q
donc
E r r E r
2
2
int
22
22
00
r
. ( ) ( )4
4
41
( )4 ( ) r
er
Pour R
E dS E r dS E r r
QR
donc
RR
E r r E r
2. Deux sphères S1 et S2 concentriques :
i) Calcul de la charge Q1 et Q2 :
2-10
1 1 1
22 -10
2 2 1 2
4 16 4 10 C
4 16 4 10 C
Q dS R Q
Q dS R R Q
ii) le champ électrique
)(rE
:
Dans la région A :
1
rR
int
1
0
( ) 0
er
Q
Er
Dans la région B :
12
R r R
0.5
0.5
0.5
0.5
0.5