Travaux Dirigés 2

Travaux Dirigés 2
Correction
A
1. Les questions 1 et 2 sont assez proches. Je répond aux deux en même temps.
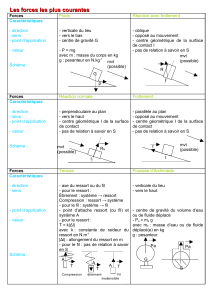
Figure 1 – Schémas du système
2. Pour donner l’expression d’une force, il faut tout d’abord définir un repére. On choisit ici un repére
Oz le long de l’axe du ressort (c’est obligatoire) et dont le vecteur unitaire est −→ uzest orienté dans la
direction du ressort (repére intelligent de la question 2). Quelque soit le sens choisi pour le vecteur,
la force de rappel d’un ressort de longueur au repos, l0et de constante de raideur k, est définie dans
le cours comme −→ F=−k(z−z0)−→ uzoù zest la coordonnée du point d’application de la force (point
A entre le ressort et la masse) et z0la coordonnée correspondant à la longueur du ressort à vide. Ici,
les coordonnées sont toutes positives. Donc z=let z0=l0. Ainsi, −→ F=−k(l−l0)−→ uz.Remarque :
Si le vecteur −→ uzavait été pris dans l’autre sens (vers le haut dans la figure ci-dessus), alors z=−let
z0=−l0. Ainsi, −→ F= +k(l−l0)−→ uz. Dans la pratique, il est souvent plus sage de laisser les formules
avec les coordonnées zet de seulement faire attention à l0.
3. L’origine du repère est pris en O, on note zla côte de la masse. À vide, la côte du point A est z0à
vide et de zavec la masse. La force de rappel du ressort est donc −→ F=−k(l−l0)−→ uz=−k(z−z0)−→ uz.
On vérifie bien ainsi que plus on tire vers le bas, plus le ressort exerce une force importante dirigée
vers le haut.
4.
Par analyse dimensionnelle : on doit avoir le poids qui est compensé par la force de rappel. La question
est : quelle sont les grandeur qui vont intervenir dans l’allongement ? Plus le système a une grande
masse, plus le ressort s’allonge. En outre plus le ressort est souple (kpetit), plus le ressort s’allonge.
Enfin, plus l’attraction de la Terre est grande, donc gest grand, plus le ressort s’allonge. La formule
fait donc intervenir la masse, m, la constante de raideur k, et enfin la constante de gravitation de la
terre g.
On cherche un allongement, ∆l, c’est donc une longueur de dimension L, qui est liée à une masse m
de dimension M, à une constante de raideur ket à g. On suppose donc que 4l=Kmαkβgγ.Kest
une grandeur sans dimension. On note les dimensions d’une variable physique avec des crochets. La
dimension de ∆ls’écrit [∆l]. Ainsi [∆l] = [m]α[k]β[g]γNotez que la constante sans dimension Ka
disparu dans l’équation aux dimensions.
–kest présent dans la formule F=kl Donc kest une force divisée par une longueur. Une force est
une masse multipliée par une accélération (Newton). Donc [k]=[F]/L ={M.(L/T 2)}/L =M/T 2
1

2
–gest présent dans la formule P=mg donc gcorrespond à une force divisée par une masse. D’après
la loi de Newton, F=ma cela correspond à une accélération. Donc la dimension de gest L.T −2
L=Mα(M.T −2)β(L.T −2)γ
On écrit alors un système pour les 3 dimensions L, M et T :
– Pour que l’égalité soit vraie pour la dimension L : γ= 1
– Pour que l’égalité soit vraie pour la dimension M : 0 = α+β
– Pour que l’égalité soit vraie pour la dimension T : 0 = −2β−2γ
– soit α= 1,β=−1,γ= 1,∆l∝mg
k
En utilisant le Théorème du centre d’inertie, on a pour le système {masse} le poids qui est compensé
par le force de rappel du ressort comme indiqué sur le schémas. Dès lors d’après :
X−→
Fext =−→ P+−→ F=−→ 0
en projetant suivant l’axe z, on a (attention P et F sont des grandeurs algébriques qui peuvent
être positives ou négatives. Par contre ket gpar exemple sont des grandeurs numériques, toujours
positives...
F+P= 0
−k(z−z0) + mg = 0
z−z0=mg
k
On retrouve bien le même résultat, mais on connait maintenant la constante. On peut aussi vérifier
que z−z0>0donc zcorrespond à une coordonnée plus grande, donc plus bas que z0ce qui est
normal !
B
Figure 2 – Schémas des forces sur la voiture
1. Dans cette question, la voiture est à l’arrêt. Il n’y a donc pas de force de frottement à considérer. La
réaction du support est uniquement normale. Les forces s’appliquant à la voiture sont, le poids du
véhicule −→ P, la réaction −→ Rdu support (le sol) normale −→ Rn.
2. Ici, il faut décomposer la question.
(a) Tout d’abord, on cherche une puissance, qui est une énergie fournie divisé par un temps. Donc
on va d’abord chercher l’énergie à fournir.
(b) L’énergie est en fait le travail Wque la force de poussée va fournir. On s’intéresse à un travail
entre deux points. On va donc appliquer le TEC ou le théorème de l’énergie mcanique. Il faut
donc s’intéresser aux forces et à leur travail.
(c) Le poids est une force conservative, elle intervient dans l’énergie potentielle uniquement. Ep=
mgz en ayant fait bien attention de prendre un axe Oz orienté vers le haut. Ensuite, la réaction
est toujours perpendiculaire au mouvement, son travail est nul. Enfin, la force de poussée ne
peut pas être considérée comme une force conservative. Essentiellement car on ne connait pas
son expression !

3
(d) On va donc exprimer la variation de l’énergie mécanique entre l’instant 0 (v= 0et z=z0) et
l’instant t(v= 0 à nouveau et z=z0+ ∆zcorrespondant à une longueur L0. On applique le
théorème de l’énergie mécanique, avec une force dissipative :
∆Em=W
∆Ec+ ∆Ep=W
La variation d’énergie cinétique est nulle puisque (vf inale =vinitiale):∆Ec= 0. La voiture
en parcourant la distance L0voit son énergie potentielle varier de ∆Ep=mg∆zdans laquelle
∆z=L0sin(45°) = ∆z=L0√2
2.
(e) La puissance à dépenser se déduit alors
W=P×T0
mgL0
√2
2=P×T0
P=mgL0
√2T0
(f) Il faut noter que nous n’avons pas eu besoin de préciser si la force de poussée était constante ou
non. Seul compte l’état de la voiture (position et vitesse) au début et à la fin du mouvement.
C
1. ω= 2π/T est en rad.s−1. La période correspond au nombre de seconde pour faire un tour (2πrad).
La pulsation correspond au nombre de radian parcouru en une seconde (faites une régle de trois...).
Le rad est un angle, dont la mesure correspond à un rapport de longeur, ce qui n’a pas d’unité. Donc
$est homogéne à l’inverse d’un temps, s−1. Ensuite gest en m.s−2et len m, du coup :pg
/lest en
pm.s−2
/m=s−1. La formule est homogène. Par ailleurs si g= 0 (cas extrême de l’apesanteur), il n’y
aura pas d’oscillation donc ω= 0. Cela “démontre” que gdoit bien être au numérateur dans cette
formule.
Si la corde du pendule est plus grande, le mouvement de balancier prend plus de temps car le bout
du pendule parcourt une plus grande distance ; laugmente implique que ωdiminue, ce qui est bien
le cas avec la formule.
2. La justification est toujours complexe. Mais on peut tenir un peu près le raisonnement suivant... Si
le ressort est vertical, on doit avoir le poids qui est compensé par la force de rappel dans la position
au repos. Mais la masse intervient dans la formule de Newton, donc il est raisonnable de penser
qu’elle intervient dans la période. En outre plus le ressort est raide (kgrand), moins la masse va être
autorisée à s’éloigner, on peut donc penser que la période sera plus courte (donc la pulsation plus
faible). Enfin, plus l’attraction de la Terre est grande, donc gest grand, plus le ressort s’allonge et la
pulsation change, gpeut aussi intervenir à priori. Au final, $∝mαkβgγ. En procédant par analyse
dimensionnelle :
T−1= [m]α[k]β[g]γ
T−1=Mα(M.T −2)β(L.T −2)γ
T−1= (M)α+βLγT−2(β+γ)
Soit −1 = −2(β+γ); 0 = α+β; 0 = γ,pour T, M et L. Donc γ= 0puisβ=1 /2et enfinα=−1 /2,
ω∝pk /m.
En fait le système ne dépend pas de la gravité. En soit cela est logique, car en apesanteur, la force du
ressort est toujours présente, donc les oscillations auront toute de même lieu... Enfin, comme nous
le pensions au dé’but, si le ressort est tout mou, kest faible, le mouvement sera très lente, donc
la période grande et la pulsation faible... le cas extrême étant en l’absence de ressort (k= 0), pas
d’oscillation ω= 0 ! La formule est cohérente.
D
1. Une pression, c’est une force par unité de surface =F
S≡kg.m.s−2 m2=kg.m−1.s−2.
–Y=ραvβ≡(kg.m−3)α(m.s−1)β=kgαm−3α+βs−β
d’où α= 1 et β= 2, résultat classique d’hydrodynamique (fin du semestre ; Bernoulli)

4
–Y=ργgδz≡(kg.m−3)γ(m.s−2)δm=kgγm−3γ+δ+s−2δ
d’où γ= 1,δ= 1 et = 1 : résultat classique d’hydrostatique (fin du semestre)
2. Pour démontrer la cohérence, il faut mieux utiliser les dimensions. On écrit ici les unités entre crochets
pour exprimer la dimension...
(a) [kJ.s−1]≡E/t soit une puissance, dont une unité est le mW donc ok. Pour faire la conversion
d’une unité vers une autre, il faut revenir aux unités standard : 1mW = 10−3W= 10−3J.s−1=
10−3(10−3kJ).s−1= 10−6kJ.s−1
(b) [mg.cm2.s−3] = ML2T−3= (M LT −2)(LT −1)=[F L/T ] = W
t= [kJ.s−1]...ok. 1mg.cm2.s−3=
10−6kg.10−4m2.s−3(attention, l’unité de masse est le kg ). 1 mg.cm2.s−3= 10−10kg.m2.s−3.
Etant dans les unités standards, on peut dire que 1 kg.m2.s−3= 1 J/s = 10−3kJ/s. Donc 1
mg.cm2.s−3= 10−1010−3kJ.s−1= 10−13kJ/s ATTENTION : ERREUR DANS L’ENONCE...
3. 1
H0≡m km.s−1∝sc’est homogène à un temps : Ok !
On transforme H0en unité mks, soit HO=70×103 /3×1022 = 2.33×10−18s−1, d’où 1 /H0= 428.571015s.
Il y a 86400sdans une journée, soit 31.55 ×106sdans une année. 1 /H0=5×1015 /32×106'15 ×109
années, l’ordre de grandeur donné sur la feuille.