TS Spécialité Physique Télescope modélisé Exercice résolu

P a g e | 1
Télescope modélisé Document : M.Moppert - CPF - Beyrouth
TS
Spécialité
Physique Télescope modélisé Exercice
résolu
Enoncé
Remarques :
- Le schéma en annexe (à compléter au fur et à mesure de l’avancement de l’exercice) est un
schéma de principe qui ne respecte pas d’échelle.
- Compte tenu des faibles valeurs des angles et de l’incertitude sur les mesures, on pourra
écrire : tan α
= α (rad).
• Définition : le pouvoir séparateur d’un instrument d’optique mesure le plus petit angle séparant
deux points que l'on parvient à voir comme distincts l'un de l'autre, avec cet instrument.
• Proposition : il n’est pas possible, à l’œil nu, de séparer les graduations millimétriques d’une
règle graduée éclairée située à une distance D = 4,0 m de cet œil .
1. a) Déterminer le diamètre apparent θ de l’objet défini comme un segment AB = 1,0 cm de la
règle.
b) Vérifier que la proposition précédente est vraie pour un œil normal dont le pouvoir séparateur
est ε = 3,0 x 10-4 rad.
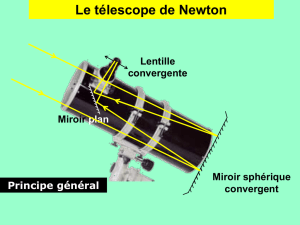
2. À l’aide d’un banc d’optique, on réalise un modèle de télescope de type Newton qui utilise pour
objectif un miroir sphérique convergent (M1) de centre C, de rayon de courbure r = 600 mm. Le
pied A de la règle objet AB précédente est alors situé sur l’axe optique de l’objectif à la distance
D = 4,30 m du sommet S du miroir. A cette distance, on considère que l’objet AB est à l’infini et
qu’il est vu à l’œil nu sous l’angle θ calculé dans la première question.
a) Justifier que la distance focale f’1 de l’objectif soit égale à 300 mm.
b) Où l’image A1B1 donnée par l’objectif va-t-elle se former ?
c) Sur le schéma de l’annexe on a commencé à tracer un rayon (R) issu de B. A partir de ce rayon,
construire l’image A1B1 et calculer la taille de cette image après avoir placé l’angle θ.
3. Cette image ne peut pas être observée directement. Pour y remédier, on place sur l’axe du
miroir sphérique, à 280 mm du sommet S, un petit miroir plan (M2) de centre C’ (point déjà placé
sur le schéma) qui réfléchit la lumière dans une direction perpendiculaire à l’axe optique de
l’objectif (le miroir plan est incliné d’un angle α = 45° par rapport à l’axe optique de l’objectif).
a) Déterminer la taille de l’image A2B2 donnée par le miroir plan et la distance C’A2.
b) Sur le schéma de l’annexe, placer le miroir plan et construisez l’image A2B2.
c) Pourquoi faut-il que le miroir plan soit de petites dimensions ?
4. On observe l’image A2B2 à l’aide d’un oculaire : lentille convergente (L) de centre optique O2,
de foyers F2 et F’2 et de distance focale f’2 = + 50 mm. La mise au point est faite de telle façon
qu’un œil normal puisse observer l’image définitive A’B’ donnée par la lentille sans accommoder.
a) Comment faut-il placer la lentille pour obtenir ce résultat ? Déterminer la distance O2A2.
b) Compléter le schéma de l’annexe en plaçant la lentille (L), ses foyers, et en traçant la marche
du rayon (R) à travers le télescope. Indiquer clairement où se trouvent les points A’ et B’.
c) Comment peut-on qualifier ce télescope ?

P a g e | 2
Télescope modélisé Document : M.Moppert - CPF - Beyrouth
5. a) Sur le schéma de l’annexe, placer l’angle θ’ sous lequel l’observateur voit l’image finale A’B’.
Calculer cet angle. L’observateur peut-il alors distinguer les graduations millimétriques de la
règle objet ?
b) En déduire le grossissement G du dispositif et le comparer au rapport
'
1
'
2
f
f
.
c) Quand la planète Mars est au plus près de la Terre, elle est vue à l’œil nu sous le diamètre
apparent θm = 1,4 x 10-4 rad. Sous quel angle θ’m son image sera-t-elle vue avec le télescope ?
Pourra-t-on alors distinguer nettement les contours de la planète ?

P a g e | 3
Télescope modélisé Document : M.Moppert - CPF - Beyrouth
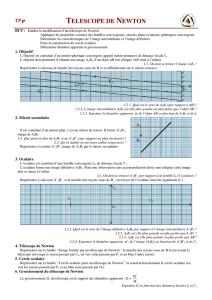
Annexe
S
F’
1
(R)
C’

P a g e | 4
Télescope modélisé Document : M.Moppert - CPF - Beyrouth
A
B
D
θ
θθ
θ
Corrigé
1. a) Déterminer le diamètre apparent θ
θθ
θ de l’objet défini comme un segment AB = 1,0 cm de la règle.
tan θ =
AB
D
et tan θ = θ (rad) => θ =
AB
D
Soit : θ
θθ
θ =
2
1,0
4,0 10
×= 2,5 x 10-3 rad
b) Vérifier que la proposition précédente est vraie pour un œil normal dont le pouvoir séparateur
est ε
εε
ε = 3,0 x 10
-4
rad.
Si le diamètre apparent d’un objet de 1,0 cm est 2,5 x 10-3 rad, le diamètre apparent d’une
graduation millimétrique est 10 fois plus petit soit égal à 2,5 x 10-4 rad. On constate que
ε > 2,5 x 10-4 rad : l’œil ne peut donc pas séparer les graduations millimétriques, ce qui confirme
la proposition précédente.
2. a) Justifier que la distance focale f’
1
de l’objectif soit égale à 300 mm.
La distance focale d’un miroir concave est égale à la moitié de son rayon de courbure : f’1 =
r
2
Soit : f’1 =
600
2
= 300 mm
b) Où l’image A
1
B
1
donnée par l’objectif va-t-elle se former ?
Un miroir concave donne d’un objet situé à l’infini une image placée dans son plan focal. Le pied A1
de l’image est donc confondu avec F’1.
c) Sur le schéma de l’annexe on a commencé à tracer un rayon (R) issu de B. A partir de ce rayon, construire
l’image A
1
B
1
et calculer la taille de cette image après avoir placé l’angle θ.
θ.θ.
θ.
Construction de A1B1 : voir schéma.
tan θ =
1 1
'
1
AB
f
= θ (rad) => A1B1 = θ.f’1 soit : A1B1 = 2,5 x 10 -3 x 300 = 7,5 x 10-1 mm
3. a) Déterminer la taille de l’image A
2
B
2
donnée par le miroir plan et la distance C’A
2
L’image A2B2 est symétrique de A1B1 par rapport au miroir plan. On en déduit que leurs
dimensions sont les mêmes : A2B2 = A1B1 soit : A2B2 = 7,5 x 10-1 mm.
Par symétrie, on constate que C’A2 = C’F’1 => C’A2 = SF’1 – SC’ soit C’A2 = 300 – 280 = 20,0 mm.
b) Sur le schéma de l’annexe, placer le miroir plan et construisez l’image A
2
B
2
.
Voir schéma.
c) Pourquoi faut-il que le miroir plan soit de petites dimensions ?
De telle façon qu’un minimum de rayons entrant dans le télescope soit arrêté.
4. a) Comment faut-il placer la lentille pour obtenir ce résultat ? Déterminer la distance O
2
A
2
.
Un œil normal observe sans accommoder (et donc sans fatigue) à l’infini. Pour cela, l’objet A2B2
(pour l’oculaire) doit être placé dans le plan focal objet de cette lentille.
On doit donc avoir O2A2 = f’2 soit : O2A2 = 50 mm.
b) Compléter le schéma de l’annexe en plaçant la lentille (L), ses foyers, et en traçant la marche du rayon (R) à
travers le télescope. Indiquer clairement où se trouvent les points A’ et B’.
Voir schéma.
c) Comment peut-on qualifier ce télescope ?
Ce télescope est afocal : il donne d’un objet à l’infini une image à l’infini.

P a g e | 5
Télescope modélisé Document : M.Moppert - CPF - Beyrouth
5. a) Sur le schéma de l’annexe, placer l’angle θ
θθ
θ’ sous lequel l’observateur voit l’image finale A’B’. Calculer cet
angle. L’observateur peut-il alors distinguer les graduations millimétriques de la règle objet ?
tan θ’ =
2 2
'
2
A B
f
et tan θ’ = θ’ (rad) => θ’ =
2 2
'
2
A B
f
soit : θ
θθ
θ’ =
1
7,5 10
50
−
×= 1,5 x 10-2 rad.
Si le diamètre apparent de l’image A’B’ est de 1,5 x 10-2 rad, le diamètre apparent d’une
graduation millimétrique est 10 fois plus petit soit égal à 1,5 x 10-3 rad. On constate que ε < 1,5 x
10-3 rad : l’œil peut donc distinguer les graduations millimétriques de la règle objet.
b) En déduire le grossissement G du dispositif et le comparer au rapport
'
1
'
2
f
f
.
G =
'
θ
θ
soit G =
2
3
1,5 10
2,5 10
−
−
×
×= 6,0. Par ailleurs :
'
1
'
2
f
f
=
300
50
= 6,0. On a bien G =
'
1
'
2
f
f
c) Quand la planète Mars est au plus près de la Terre, elle est vue à l’œil nu sous le diamètre apparent
θ
θθ
θ
m
= 1,4 x 10
-4
rad. Sous quel angle θ
θθ
θ’
m
son image sera-t-elle vue avec le télescope ? Pourra-t-on alors distinguer
nettement les contours de la planète ?
G =
'
θ
θ
m
m
=> θ’m = G.θm soit θ
θθ
θ’m = 6,0 x 1,4 x 10-4 = 8,4 x 10-4 rad. On constate que θ’m > ε : ce
télescope permet de distinguer nettement les contours de Mars.
S
F’
1
(R)
C’
A
1
B
1
F2-A2
B
2
O
2
F’
2
B’
∞
A
’
∞