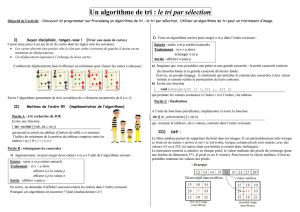
Chapitre 4. Diviser pour régner. Retour. I Maximum d'un tableau

b√nc
a0;a1;···;an−1n
b0;b1;···;bn−1bm=a0
∀i < m, bi6bm∀i > m, bi> bm
b0;b1;···;bm−1bm+1;b1;···;bn−1
x= (x1, ..., xn)x
(i, j i < j xi> xj(2,3,1,5,4)
(1,3),(2,3),(4,5)
O(n2)