Aide à la résolution de circuits électriques Le circuit électrique

ECAM
1
Aide à la résolution de circuits électriques
Le circuit électrique
Un circuit électrique est un graphe dont :
Chaque nœud représente un potentiel
Chaque arc est porteur d’un courant
Il s’en suit que chaque arc est compris entre deux potentiels  il existe une différence de
potentiel aux bornes de l’arc.
Voici un exemple où l’on voit un courant d’un ampère
circuler entre trois potentiels.
Un nœud n’est pas une source ou un puits de courant, il
représente seulement un potentiel. Il est donc logique
que seuls les graphes bouclés sont susceptibles de
permettre la circulation d’un courant.
C’est la raison pour laquelle on parle de « circuit
électrique » pour désigner les cas pratiques.
Cependant, un graphe qui ne montre que des courants et
des potentiels ne présente pas l’ensemble des informations du circuit car il y a en plus des
contraintes. Les contraintes viennent de la nature des composants mais aussi des grandeurs
physiques manipulées.
Contraintes liées aux grandeurs électriques
Bien souvent dans les graphes, les nœuds sont porteurs de grandeurs extensives, qui sont liées
à une position dans l’espace.
Parmi ces grandeurs, on rencontre les tensions électriques qui sont l’expression de l’énergie
potentielle, du travail qu’il faudrait fournir à une charge électrique unitaire pour l’amener
d’un point situé à l’infini vers la position du nœud. Le cours d’électricité montre que cette
valeur dépend d’une constante d’intégration que l’on peut choisir arbitrairement. C’est
pourquoi, on se choisit un potentiel de référence à 0V parmi les nœuds du graphe. Ce qui va
compter par la suite, ce sont les différences de potentiel.
A tout instant, chaque nœud n’a qu’un et un seul potentiel. Dès lors, tout chemin dans le
graphe qui part de ce nœud et y revient, revient au potentiel de son point de départ.
3V
6V
0V
1A
1A
1A

ECAM
2
Ce qui va donner lieu à la première loi fondamentale des circuits électriques :
Loi des mailles = la différence de potentiel aux extrémités d’une
maille (boucle dans le graphe) est toujours zéro.
Autrement dit, la somme des différences de potentiels le long d’une maille est nulle.
De leur côté, les arcs de bien des graphes sont liés à des grandeurs intensives, soumises à un
principe de conservation.
La grandeur conservée est ici la charge électrique dont le courant est la dérivée par rapport au
temps.
Comme les nœuds du graphe n’absorbent pas et ne créent pas de charge, toute charge entrante
doit instantanément sortir par un autre chemin. C’est la seconde loi des circuits électriques :
Loi des nœuds = la somme des courants incidents à un nœud
est toujours zéro.
Ces deux lois sont inhérentes au système de représentation, le graphe que nous avons choisi,
et qui correspond aussi à ce que nous enseigne la théorie de l’électricité pour les phénomènes
électriques vus à l’échelle que nous voulons étudier.
Contraintes liées aux composants
La nature des composants d’un circuit électrique est exprimée par une équation de contrainte
qui relie entre elles ses grandeurs électriques :
- la différence de potentiel à ses bornes,
- le courant qui le traverse.
On appelle cette équation « l’équation d’état » du composant et le terme « variables d’état »
désigne son courant et la différence de potentiel à ses bornes. Or c’est une erreur courante à
l’examen que de mélanger le U et le I de branches qui n’ont rien à voir avec le composant !
On peut exprimer la contrainte de plusieurs manières :
Par un symbole spécifique dans le circuit,
Par une équation mathématique U=f(I) ou I=f(U),
Par une courbe dans un diagramme (U,I) ou (I,U).
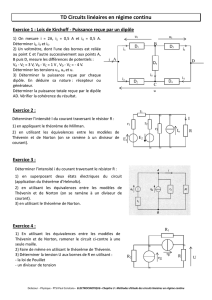
Voici un tableau des contraintes élémentaires :
On y constate qu’un fil est équivalent à une résistance nulle.
On remarquera aussi les sens opposés de U et I autour de la résistance. En effet, ce
composant est passif et consomme l’énergie fournie par les sources du circuit. Le produit UI,
qui est l’expression de la puissance consommée, est ainsi négatif.

ECAM
3
Ua Ub
=
L’équipotentielle représente
un conducteur dans le
circuit : par exemple un fil.
3
I A
=
La source de courant impose
un courant dans la branche
quelque soit la tension à ses
bornes.
20
Ub Ua V
= +
La source de tension impose
une différence de potentiel
entre ses bornes quelque soit
le courant qu’elle devra faire
passer.
U RI
=
La résistance, ici de 10 ohms,
impose un rapport constant
entre U et I
Voici la représentation de ces composants dans un diagramme (U,I) où l’on constate que la
caractéristique d’un fil se confond avec l’axe des courants :
Ua Ub
3A
20V
Ua Ub
10Ω
U
I
I
U
U = constante
I = constante
U = 0V
U = R I

ECAM
4
Réalisation et résolution de circuits
Pendant la phase d’analyse :
Les réseaux et appareillages électriques sont des entités physiques peu adaptés pour
leur analyse. On passe d’abord par un intermédiaire de représentation du système.
La modélisation d’un réseau électrique est un graphe qui représente ce réseau en
mettant en avant ses caractéristiques électriques.
La résolution du modèle consiste à retrouver le circuit électrique, c'est-à-dire les
tensions et les courants compatibles avec les contraintes du modèle.
Pendant la phase de conception :
On part du circuit pour imaginer un ensemble de contraintes dont la résolution donne
le circuit de départ.
On appelle cette étape la réalisation du circuit. Elle mène à un modèle, un plan.
L’étape suivante est la construction du système physique en respectant les données du
plan.
L’objet des exercices de 1BA est la résolution de modèles de réseaux électriques. On parlera
plus facilement de résolution de circuits électriques.
Mise en série, mise en parallèle.
La différence entre grandeur intensive et extensive apparaît lors des compositions
élémentaires dont voici les tableaux.
Le courant est une grandeur intensive soumis à une loi de conservation. On peut additionner
deux courants en un point
réalisation construction
circuit plan
Système
réel
modélisation résolution

ECAM
5
redondance
addition
contradiction
Les tensions sont des grandeurs extensives. Elles dépendent de leur position dans l’espace (et
donc dans le réseau) et ne peuvent s’additionner en un point.
redondance
addition
1A 1A 1A
1A
1A
2A
1A 2A
Impossibilité
1V
1V
1V
1V 1V 2V