Annexe à rendre avec la copie - Meck

Exercice n°1 : le pur son de Lucien
1/ Lorsqu’un récepteur mobile s’éloigne d’un émetteur d’ondes fixe à la vitesse u, la fréquence apparente
mesurée est différente de la fréquence réelle émise et telle que :
où fE est la fréquence de l’onde émise (en Hz)
fR est la fréquence apparente reçue (en Hz)
v est la vitesse de l’onde dans le milieu considéré (en m.s-1)
1.1/ Comment appelle-t-on cet effet ?
1.2/ En rappelant la relation entre célérité, fréquence et longueur d’onde, établir la relation entre λE et λR.
où λE est la longueur d’onde de l’onde émise (en m)
λR est la longueur d’onde de l’onde perçue par le récepteur (en m)
2/ Lucien, en concert, frappe la deuxième corde de sa guitare et émet un
son que l’on considèrera pur, de fréquence f = 110 Hz.
De plus, Lucien porte un pull à rayures bleues. On considèrera que la
lumière diffusée par ces rayures bleues est monochromatique et de
longueur d’onde λ = 450 nm.
Lucien jouant trop fort, un spectateur, Régis, s’éloigne de la scène (et donc des hauts parleurs) à la vitesse
constante notée u = 0,750 m.s-1.
2.1/ Calculer fR pour le son et λR pour la lumière (perçus par Régis), en considérant Lucien immobile par rapport
à la scène.
2.2/ La variation de fréquence du son sera-t-elle perceptible pour Régis ? Justifier.
2.3/ La variation de longueur d’onde de la lumière bleue diffusée sera-t-elle perceptible par Régis ? Justifier.
3/ Après son concert, Lucien, apprenti astronome, observe le ciel étoilé. Il choisit une étoile et mesure grâce
aux raies d’absorption de son spectre un décalage des longueurs d’ondes perçues : λR est plus grande que λE et
le rapport vaut 5,1%.
3.1/ L’étoile considérée s’approche-t-elle ou s’éloigne-t-elle de la Terre ?
3.2/ A quelle vitesse par rapport à la Terre ?
Données :
 Célérité du son dans l’air : v = 340 m.s-1
 Célérité de la lumière dans le vide : c = 3,00.108 m.s-1
 Limite de perception par l’Homme d’une variation de fréquence sonore : ∆f > 1,0 Hz
 Limite de perception par l’Homme d’une variation de longueur d’onde pour la lumière : ∆λ > 10 nm
Exercice n°2 : Diffraction
Objet diffractant Figure de diffraction
On réalise une expérience de diffraction à l'aide d'un laser émettant une lumière monochromatique de longueur
d'onde λ. À quelques centimètres du laser, on place successivement des fils verticaux de diamètres connus. On
désigne par « a » le diamètre d'un fil.
DS N°02
PHYSIQUE -CHIMIE
1h (calculatrice autorisée)
TS1
L

La figure de diffraction obtenue est observée sur un écran blanc situé à une distance D = 1,60 m des fils. Pour
chacun des fils, on mesure la largeur « L » de la tache centrale. À partir de ces mesures et des données, il est
possible de calculer l'écart angulaire « θ » du faisceau diffracté (voir figure 1 ci-après).
2.1 Influence de la largeur de la fente sur la largeur de la tâche centrale de diffraction
2.1.a/ L'angle  étant petit,  étant exprimé en radian, on a la relation : tan  ≈ .
Donner la relation entre L et D qui a permis de calculer  pour chacun des fils.
2.1.b/ On rappelle la relation liant , λ et a :   
 Préciser les unités de , λ et a.
2.1.c/ On trace la courbe  = f(1/a). Celle-ci est donnée sur la figure 2 ci-dessus.
Montrer que la courbe obtenue est en accord avec l'expression de  donnée à la question 2.1.b
2.1.d/ Comment, à partir de la courbe précédente, pourrait-on déterminer la longueur d'onde λ de la
lumière monochromatique utilisée ? En utilisant la figure 2, calculer cette longueur d’onde. Quelle est la
couleur de la lumière émise par ce laser : rouge, vert ou violet ?
2.2 Influence de la longueur d’onde de la lumière utilisée sur la largeur de la tâche centrale
Quatre figures de diffraction sont obtenues successivement avec quatre lasers différents :
 figure n°1 obtenue avec un laser rouge ( = 630 nm ; D = 1,50 m ; a = 40 m)
 figure n°2 obtenue avec un laser jaune ( = 560 nm ; D = 1,50 m ; a = 40 m)
 figure n°3 obtenue avec un laser vert ( = 520 nm ; D = 1,50 m ; a = 40 m)
 figure n°4 obtenue avec un laser bleu ( = 455 nm ; D = 1,50 m ; a = 40 m)
A partir des figures de diffraction obtenues, vérifier la cohérence de la formule    
 quant à l’influence
de la longueur d’onde λ sur la largeur de la tâche centrale. La rédaction devra faire apparaître clairement la
démarche suivie et les résultats obtenus, dont la précision pourra être évaluée.
On pourra s’aider, si nécessaire, de l’annexe prévue pour l’exercice
2.3. Diffraction en lumière blanche
Si l'on envisageait de réaliser la même étude expérimentale en utilisant une lumière blanche, qu’observerait-
on ? Justifier la réponse.
Figure 2
Figure 1

ANNEXE A RENDRE AVEC LA COPIE
ANNEXE A RENDRE AVEC LA COPIE
NOM :
Prénom :
NOM :
Prénom :

Exercice n°2 BIS: lumière monochromatique au passage d’un obstacle
1. Observation du phénomène de diffraction
On utilise un laser (voir schéma suivant) produisant une lumière de longueur d'onde placé devant une fente de
largeur « a » (document 1). Sur un écran placé à la distance « D » de la fente, on observe une figure de
diffraction constituée de tâches lumineuses (document 2).
Objet diffractant (doc.1) Figure de diffraction (doc.2)
La largeur de la tache centrale d sur l'écran varie lorsque l'on fait varier la distance D entre la fente et l'écran, la
longueur d'onde λ de la lumière, ou la largeur a de la fente. Une série d'expériences effectuées montrent que d
est proportionnelle à la longueur d'onde de la lumière.
1.2. On propose les formules (1), (2), (3), (4) et (5) ci-dessous.
Laquelle ou lesquelles peut-on éliminer ? Justifier chaque réponse.
(1)    
 (2)      (3)      (4)      (5)      
2. Influence de la largeur de la fente
Tous les autres paramètres restant inchangés pendant les mesures, on fait varier la largeur a de la fente et on
mesure les valeurs de d correspondantes. Les résultats sont consignés dans le tableau suivant.
a (en µm)
100
120
200
250
300
340
d (en mm)
19
16
10
7,5
6,5
5,5
Préciser laquelle (ou lesquelles) des formules proposées à la question 1.2 est (sont) encore possible(s). Justifier
la réponse.
3. Influence de la distance D entre la fente et l’écran
On fixe λ et a. On déplace l'écran et on obtient les résultats suivants :
D (en m)
1,70
1,50
1,20
1,00

d (en mm)
21
19
15
13
3.1. Quelle courbe est-il judicieux de tracer pour vérifier la réponse à la question précédente ? Justifier.
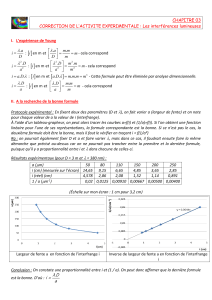
3.2. Tracer cette représentation graphique sur l’ANNEXE (à rendre avec la copie).
3.3. Calculer le coefficient directeur k de la droite obtenue.
3.4. En déduire la valeur de la longueur d’onde , sachant que l'on a fait les mesures pour a = 100 μ m.
Quelle est la couleur de la lumière émise par ce laser : rouge, vert ou violet ?
4. Détermination d’une petite dimension par application du phénomène
Un fil placé à la position exacte de la fente du dispositif précédent produit exactement la même figure sur l'écran.
Des élèves disposant d'une diode laser (λ = 633 nm) décident de mettre en œuvre cette expérience pour mesurer
le diamètre a d'un cheveu qu'ils ont placé sur un support. Ils obtiennent une tâche centrale de largeur d = 22 mm
lorsque l'écran est à D = 1,50 m du cheveu.
4.1. Calculer le diamètre du cheveu (le cheveu joue un rôle analogue à celui de la fente).
ANNEXE A RENDRE AVEC LA COPIE