Sadiki Cherchari Ke=10

1/3 4ème Maths
Collège Sadiki
Devoir de contrôle n° : 3
Sciences physiques
4ème Maths
Dimanche 09 -04-2017
Profs : Hrizi-Abid-Fkih-Medyouni et
Cherchari
Durée : 2h30 heures
Toutes les solutions sont prises à 25°C, température à laquelle le produit ionique de l’eau pure est Ke=10-14.
On dispose au laboratoire de chimie du collège Sadiki d’une solution aqueuse S1 d’un monoacide AH de
concentration molaire C1, on prélève un volume V1=10 mL de cette solution qu’on verse dans un bécher. Le
dosage pH-métrique de S1 par une solution aqueuse SB1 d’hydroxyde de potassium KOH (base forte), de
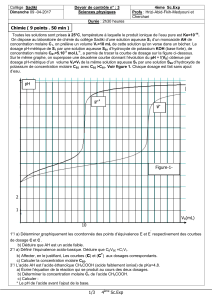
concentration molaire CB1=5.10-3 mol.L-1, a permis de tracer la courbe de dosage sur la figure ci-dessous.
Sur le même graphe, on superpose une deuxième courbe donnant l’évolution du pH = f(VB) obtenue par
dosage pH-métrique d’un volume V2=V1 de la même solution aqueuse S1 par une solution SB2 d’hydroxyde de
potassium de concentration molaire CB2 avec CB2 >CB1. Voir figure 1. Chaque dosage est fait sans ajout
d’eau.
1°/ a) Déterminer graphiquement les coordonnés des points d’équivalence E et E’ respectivement des courbes
de dosage C et C’.
b) Déduire que AH est un acide faible.
2°/ a) Définir l’équivalence acido-basique. Déduire que CBVBE =C1V1.
b) Affecter, en le justifiant, Les courbes (c) et (c’) aux dosages correspondants.
c) Calculer la concentration molaire CB2.
3°/ L’acide AH est l’acide éthanoïque CH3COOH (acide faiblement ionisé) de pKa=4,8.
a) Écrire l’équation de la réaction qui se produit au cours des deux dosages.
b) Déterminer la concentration molaire C1 de l’acide CH3COOH.
c) Calculer :
* Le pH de l’acide avant l’ajout de la base.
1
2
C
C ’
10
Vb(mL)
pH
Figure-1-
Chimie ( 7 points . 50 min )

2/3 4ème Maths
* Le pH du mélange à l’équivalence pour chaque dosage.
4°/ On réalise chaque dosage en présence d’un indicateur coloré convenablement choisi parmi les suivants.
a) Rappeler la définition d’un indicateur coloré.
b) Que veut dire un indicateur coloré convenablement choisi pour un dosage acide-base
c) Faire correspondre à chaque dosage l'indicateur approprié.
5°/ A un volume Va =20 mL d’une solution d’acide éthanoïque de concentration molaire Ca =10-2 mol.L-1 on
ajoute un volume V2 d’une solution d’éthanoate de sodium (Na+ + CH3COO-) de concentration molaire
C2=5.10-3 mol.L-1 et quelques gouttes de rouge de méthyle.
a) Pour quelle valeur de V2 le pH de la solution est égal à 4,8.
b) Donner la couleur de la solution.
c) Calculer la concentration molaire de chaque entité chimique présente dans le mélange.
Indicateur coloré
Teinte acide
Zone de virage
Teinte basique
Hélianthine
Rouge pH<3,2
3,2  pH 4,4
orangé
Jaune pH>4,4
Rouge de méthyle
Jaune pH<4,6
4,6  pH  6
orangé
Rouge pH>6
B.B.T
Jaune pH<6
6  pH 7,6 vert
Bleue pH>7,6
phénolphtaléine
Incolore pH<8,2
8,2 pH 10 rose clair
Rose pH>10
Exercice 1 ( 4 pts. 20 min) :
Une corde élastique homogène de longueur infinie est tendue horizontalement entre l’extrémité S d’une
lame vibrante et un point A ou se trouve un dispositif qui empêche la réflexion des ondes. Lorsque la lame
vibre, le point S effectue un mouvement rectiligne sinusoïdal d’amplitude a et de fréquence N. La corde est le
siège d’une onde progressive transversale qui se propage sans amortissement avec une célérité V=20 m.s-1.
Le mouvement de la source commence à la date t=0s à partir de sa position d’équilibre. On donne, à la date
t1, l’aspect de la corde est schématisé par
la figure 1.
1- Déterminer à partir du graphe :
a- L’amplitude a.
b- La longueur d’onde . Déduire la
fréquence N de l’onde.
c- L’abscisse xf du front d’onde à la
date t1. Déduire t1.
d- La phase initiale S. Écrire la loi
horaire de mouvement de la source
S yS=f(t).
2- Soit un point M de la corde, d’abscisse x par rapport à la source S. En appliquant le principe de
propagation, écrire l’équation horaire du mouvement du point M.
3-Déterminer les lieux des points qui, à la date t1, ont une élongation égale à :
2
a
et se déplacent dans le
sens négatif.
Exercice 2 :(2 pts. 12 min)
Un haut-parleur (HP) branché à un GBF, produit des vibrations sinusoïdales dans l'espace qui l'entoure. Un
microphone (M) est branché sur la voie B d'un oscilloscope. La voie A étant reliée au (HP) (fig-2-). On obtient
sur l'écran de l'oscilloscope les deux graphes suivants (fig-3-).
Les réglages de l'oscilloscope sont :
Sensibilité verticale : 1 div pour 1 V sur
les deux voies A et B
Balayage horizontal : 1 div pour 0,1 ms
1°/ Identifier le graphe traduisant le son
capté par le microphone ? Justifier la
réponse.
2°/ a) Calculer la fréquence du signal
émis par le GBF
b) Sachant que le son se propage
Physique (13 points )

3/3 4ème Maths
dans l’air environnant, à la célérité V = 340 m.s-1. Calculer la longueur d’onde  du son émis par le haut-
parleur.
3°/ a) déterminer le retard du signal capté par le microphone par rapport à celui émis par le (HP)
b) En déduire les distances possibles d séparant le microphone du haut-parleur (sachant que 0<d<0,2m et on
suppose que la membrane du HP coïncide avec l'origine du repère).
Exercice n °3 ( 7 pts. 68 min )
Un solide (S) de centre d’inertie G, de masse m=200 g et pouvant glisser sur un plan horizontal, est relié à
l’extrémité d’un ressort horizontal (R) de masse négligeable, de raideur k et
dont l’autre extrémité est fixe. Lorsque (S) est dans sa position d’équilibre, G
occupe l’origine du repère (O,
i
) d’axe Ox horizontal (figure 1).Un excitateur
approprié exerce sur le solide (S) une force
F
=Fm sin
t
i
où l’amplitude Fm est
constante et la pulsation
est réglable. (S) est à une force de frottement de
type visqueux
vhf 
avec h est un coefficient positif et
v
est la vitesse de G.
L’équation différentielle régissant les variations de l’élongation x(t) est
2
d x dx
m h Kx F(t)
dt dt
, dont la
solution est x(t)=Xm sin (
t)  
.
1- a- Ces oscillations sont dites forcées, expliquer ce terme.
b- Donner l’unité internationale du coefficient de frottement h.
2- a) En utilisant une construction de Fresnel, Déterminer l’expression de l’amplitude Xmax des oscillations en
fonction de Fm, h, K, m et .
b) Établir l’expression de la pulsation r à la résonance d’élongation en fonction de 0 , h et m.
3-
a- Montrer qu’à la résonance d’élongation, l’amplitude des oscillations est
2
2
02
4
e
mr Fm
Xh
hm
b- En utilisant l’analogie électrique mécanique, montrer qu’à la résonance de vitesse l’amplitude des
oscillations est
vm
mr F
Vh
4- A l’aide d’un dispositif approprié on mesure pour différentes valeurs de , l’amplitude Xm des oscillations de
G et l’amplitude Vm de la vitesse de
passage de ce point par la position
O. Les résultats des mesures ont
permis de tracer les courbes Xm()
et Vm() de la figure 2
a) Identifier en le justifiant, la
courbe qui correspond à Xm ().
b) Lire la valeur 0 de la pulsation
propre du résonateur et déduire la
valeur de k.
c) Déterminer la valeur du
coefficient de frottement h.
d) Déduire la valeur de Fm.
5- La pulsation de la force
excitatrice est égale à la pulsation
propre 0.
a- Montrer que la puissance
mécanique moyenne consommée
par le résonateur est maximale.
Calculer sa valeur.
b- Écrire, dans ces conditions
l’expression de la force de frottement f(t).
6- On change le liquide amortisseur ; on constate qu’on n’obtient plus le phénomène de résonance
d’élongation. Déterminer la valeur limite du coefficient de frottement.
Fig.
5
i
O
(S)
(R)
x
Fig 1
10
(rad.s-1)
0,046
0,4
Xm(m) ; Vm(m.s-1)
Figure-2-