Solutions Feuille de Travaux Dirigés n 6

Université Francois Rabelais de Tours
Master de Mathématiques
Solutions Feuille de Travaux Dirigés n◦6
M1, Algèbre Semestre 8
Corps finis
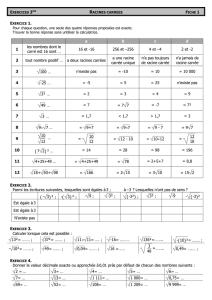
Exercice 1
1) Trouver tous les polynômes degré 4irréductibles sur Z/2Z.
Solution: Déjà fait dans un Td précédent.
2) Soit P(X) = X4+X+ 1 ∈Z/2Z[X],Lun corps de rupture de Psur Z/2Zet αune racine de P
dans L. Quel est le cardinal de L? Donner une base de Lsur Z/2Z.
Solution: Le polynôme Pest irréductible ainsi [L:F2] = 4 et |L|= 24= 16. La famille (1, α, α2, α3)
est une base de Lsur F2.
3) Montrer que αest un générateur du groupe multiplicatif (L∗,×).
Solution: Les ordres possibles pour αsont 2,4,8,16. Pour montrer que αest d’ordre 16, il suffit de
montrer que α86= 1. En effet, dans cas, on ne peut pas avoir α2= 1 ou α4= 1 puisque α8= (α2)4
et α8= (α4)2. On a
α8= (α4)2
= (α+ 1)2
=α2+α6= 1.
4) En utilisant l’automorphisme de Frobenius φdéfini par φ(x) = x2, déterminer explicitement tous les
sous-corps de L(c’est à dire expliciter leurs éléments en fonction de α).
Solution: Soit Kun sous-corps de Lqui contient F2. Alors K∗est un sous-groupe de L∗et |L∗|= 15.
Ainsi |K|= 1,3,5,15. Commençons par traiter les cas les plus simples :
(a) Si |K∗|= 15 alors K=L.
(b) Si |K∗|= 1 alors K=F2.
(c) On ne peut pas avoir |K|= 5 puisque il n’existe pas de corps à 6éléments ! (6 n’est pas une
puissance d’un nombre premier.)
Reste le cas |K∗|= 3. Puisque Kest un corps K∗est cyclique, et donc K∗est engendré par un
élément de la forme αk(1≤k≤14). On doit avoir (αk)3=α3k= 1, ce qui implique que 15 |3ket
5|k. On a donc k= 5 ou 10 et
K∗:= {1, α5, α10}.
On vérifie facilement que {0,1, α5, α10}est un sous-corps de L.
5) Justifier que Lcontient un corps de rupture du polynôme X2+X+ 1 sur Z/2Zet factoriser ce
polynôme dans L.
Solution: Il suffit de montrer que ce polynôme admet une racine dans L. On la cherche sous la
forme a+bα +cα2+dα3. Puisque a, b, c, d ∈F2, on a a2=a, b2=b, c2=cet d2=d. De plus, pour
tout (x, y)∈F2
2, on a (x+y)2=x2+y2. On calcule
P(a+bα +cα2+dα3)=(a+bα +cα2+dα3)2+a+bα +cα2+dα3+ 1
=a+bα2+cα4+dα6+a+bα +cα2+dα3+ 1
=a+bα2+c(α+ 1) + d(α3+α2) + a+bα +cα2+dα3+ 1
=c+1+α(c+b) + α2(b+d+c)
Ainsi Ps’annule en a+bα +cα2+dα3si et seulement si
c+ 1 = 0
c+b= 0
b+d+c
Padmet deux racines dans L:α+α2et 1 + α+α2
1

6) Montrer (par un argument de degré) que l’équation x3+x+ 1 = 0 n’a pas de solution dans L.
Solution: Le polynôme X3+X+ 1 = 0 est irréductible sur F2. S’il admet une racine xdans L,
alors
[F2(x) : F] = 3 et 3|[L:F2]
mais c’est impossible puisque [L:F2]=4.
7) Montrer que si x∈Lest racine de Palors φ(x)est racine de P. En déduire que Lest un corps de
décomposition de P.
Solution: On rappelle que Φest un ismorphisme de corps de Ldans Let donc
P(φ(x)) = (φ(x))4+φ(x)+1
=φ(x4+x+ 1)
=φ(0) = 0
Ainsi puisque αest racine de P, on en déduit que α2,α4et α8sont racines de P. Tous ces éléments
sont distincts puisque αest d’ordre 15. On a donc bien trouvé les 4 racines de Pdans L.
8) On considère maintenant le polynôme Q(X) = X4+X3+X2+X+ 1. Soit L0un corps de rupture
de Qsur Z/2Zet θune racine de Qdans L0. Justifier que Let L0sont des corps isomorphes.
Solution: Qest irréductible sur F2et |L0|= 16. Comme tous les corps finis de même cardinal sont
isomorphes, on a bien L'L0.
9) Est ce que θest un générateur du groupe multiplicatif (L0∗,×)?
Solution: Non. On a
θ5=θ(θ3+θ2+θ+ 1)
=θ4+θ3+θ2+θ
= 1
et θest d’ordre 5.
10) Vérifier que θ+θ2est racine de Pdans L0. En déduire un isomorphisme de corps explicite entre L
et L0.
Solution: On a
P(θ+θ2) = (θ+θ2)4+θ+θ2+ 1
=θ4+θ8+θ+θ2+ 1
=θ4+θ3+θ+θ2+ 1
= 0
Ainsi θ+θ2est racine de P. On peut vérifier que θ+θ2est d’ordre 15 et donc on peut construire
un isomorphisme de Ldans L0en posant αi7−→ (θ+θ2)i.
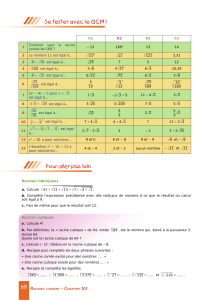
Exercice 2 Soit Fun corps fini de caractéristique pet soit f∈F[X]un polynôme irréductible. L’objectif
de cet exercice est de montrer que fest séparable, c’est-à-dire que fn’admet aucune racine multiple. On
procède par contradiction et on suppose que fadmet une racine multiple.
1) Montrer que pgcd(f, f0)6= 1.
Solution: Soit αune racine multiple de fdasn uen extension de F. On voit alors que αest aussi
racine de P0. Ainsi, le polynôme minimal de αsur Fdivise Pet P0et pgcd(f, f0)6= 1.
2) En utilisant le fait que fest irréductible, en déduire que f0= 0.
Solution: fétant irréductible, on en déuit que pgcd(f, f0)et fsont de même degré. Ainsi pour
que pgcd(f, f 0)divise f0il faut que f0= 0.
3) Montrer qu’il existe un polynôme g∈F[X]tel que f(X) = g(Xp).
Solution: La dérivé d’un terme aXkest akXk−1. Ainsi, si a6= 0, pour que f0= 0 il faut que k= 0
dans Fp. Cela implique que kest un multiple de p. Ainsi fs’écrit sous la forme
p
X
i=0
aiXip =Xai(Xi)p
et en posant g=PaiXion a le résultat.
2

4) Montrer qu’il existe h∈F[X]tel que f(X)=(h(X))p.
[On utilisera le morphisme de Frobenius x7→ xp.]
Solution: On reprend le polynôme gde la question précédente. On pose bi=φ−1(ai)où φdésigne
l’isomorphisme de Frobenius x7−→ xp. Soit h=PbiXi. On a alors
(h(X))p=XbiXip =Xbp
iXip =XaiXip =f(X).
5) Conclure.
Solution: fne peut pas être irréductible et de la forme h(X)pavec p≥2! On a obtenu une
contradiction et donc fne peut pas avoir de racine multiple.
Polynômes cyclotomiques
Exercice 3 Soit nun entier naturel. On note Φnle n-ème polynôme cyclotomique. L’objectif de l’exercice
est de démontrer que Φnest irréductible sur Q. On rappelle que si on note Un⊂Cl’ensemble des racines
n-èmes de l’unité et Pn⊂Unl’ensemble des racines n-èmes primitives, alors
Φn(X) = Y
ω∈Pn
(X−ω)∈Z[X].
Soit Pun facteur irréductible unitaire de Φnsur Qet Q= Φn/P .
1) Rappeler pourquoi Pet Qsont à coefficients entiers.
Solution: Commençons par montrer que
Xn−1 = Y
d|n
Φd.
On remarque tout d’abord que ces deux polynômes sont de même degré puisque Pd|nϕ(n) = n. Soit
ωune racine primitive de l’unité d’ordre n. Les racines de Xn−1sont donc {1,ω,...,wn−1}. Soit
0≤k≤n−1et soit dl’ordre de ωk. On a d|net donc wkest racine de Qd|nΦd.Ainsi toutes les
racines de Xn−1sont aussi racines de Qd|nΦd. Comme ces polynômes sont de même degré, on a
l’égalité souhaitée.
Montrons maintenant par récurrence que Φn∈Z[X]. C’est vrai pour n= 1. On a
Xn−1 = Y
d|n
Φd= Φn·Y
d|n,d6=n
Φd
| {z }
=P∈Z[X]
Puisque Pest unitaire, on peut effectuer la division euclidienne dans Z[X]de Xn−1par Pet par
unicité on obtient que Φn∈Z[X].
Factoriser dans Q[X]est équivalent à factoriser dans Z[X]puisque tous les polynômes en présence
sont unitaires. Ainsi P, Q ∈Z[X].
2) Soit ω∈Cune racine de Pet pun nombre premier tel que p-n. L’objectif de cette question est de
montrer que ωpest encore racine de P. On suppose par l’absurde que ωpn’est pas racine de P.
(a) Montrer que ωpest racine de Q.
Solution: Puisque p-n, la racine nième de l’unité ωpest primitive. C’est donc une racine de
Φn. Puisque
0=Φn(ωp) = P(ωp)Q(ωp)
et P(ωp)6= 0, on a Q(ωp)=0.
(b) Montrer que P(X)divise Q(Xp)dans Z[X].
Solution: Les polynômes P(X)et Q(Xp)ont une racine en commun, ils ne sont donc pas
premiers entre eux. Pétant irréductible, on en déduit que Pdivise Q(Xp).
3

(c) On note Pet Qla réduction modulo pde Pet Q. Soit Kun corps de décomposition de Psur
Z/pZet α∈Kune racine de P. Montrer que αest racine de Q.
Solution: Puisque Kest de caractéristique p, on sait que x7→ xpest un morphisme d’anneau.
Puisque Pdivise Q(Xp), on voit que Pdivise Q(Xp)et donc αest racine de Q(Xp). Mais
Q(αp) = Q(α)p
et donc αest racine de Q.
(d) En déduire que αest racine double du polynôme Xn−1∈Z/pZ[X].
Solution: On a Xn−1 = P Q et αest racine de Pet Qdonc αest racine double de Xn−1.
(e) Obtenir une contradiction.
Solution: Soit αune racine double de Xn−1. On a alors n≥2et αn= 1 et nαn−1= 0 dans
Fp. C’est impossible.
3) Soit ω∈Cune racine de Pet kun entier premier avec n. Soit k=p1···prsa décomposition en
facteurs premiers. Montrer que ωkest encore racine de P.
Solution: On procède par récurrence sur r. Si r= 1, on vient de le prouver. Supposons r > 1. Par
récurrence, puisque ωest racine de P, on sait que wp1...pr−1est aussi racine de P. On applique alors
le résultats de la question précédente à ω0=wp1...pr−1et à p=pret on voit que wp1...prest racine
de P.
4) Conclure que P= Φn.
Solution: Soit ωune racine de P. Puisque ωest aussi racine de Φn,ωest une racine primitive de
l’unité d’ordre n. D’après la question 3, tous les éléments de l’ensemble {ωk|kest premier avec n}
sont aussi racine de P. Mais
{ωk|kest premier avec n}=Pn
et donc P= Φn.
Groupe de Galois d’une extension
Exercice 4 (de cours) Le groupe de Galois d’une extension F⊂Eest défini par
Gal(E:F) := {θ:F7−→ F|θest un ismorphisme et θ(a) = apour tout a∈F}.
1) Montrer que Gal(E:F)est un groupe.
2) Soit θ∈Gal(E:F). Si t∈Eest racine de P∈F[X]alors θ(t)est aussi racine P.
Exercice 5 On considère l’extension Q⊂Q(√2) et on pose G=Gal(Q(√2) : Q).
1) Soit θ∈G. Quelles sont les valeurs possibles de θ(√2) ?
2) Déterminer G.
Exercice 6 On considère l’extension Q⊂Q(√2, i)et on pose G=Gal(Q(√2, i) : Q). Soit θ∈G.
1) Quelles sont les valeurs possibles de θ(√2) ?
Solution: θ(√2) est racine de X2−2ainsi θ(√2) = ±√2.
2) Quelles sont les valeurs possibles de θ(i)?
Solution: θ(i)est racine de X2+ 1 ainsi θ(i) = ±i.
3) Déterminer G.
Solution: D’après les questions précédentes, on voit que |G|= 4. Les éléments de Gsont :
θ1:√27−→ √2
i7−→ i
θ2:√27−→ −√2
i7−→ i
θ3:√27−→ √2
i7−→ −i
θ4:√27−→ −√2
i7−→ −i
Reste à déterminer si G'C4ou G'C2×C2. On vérifie que tous les éléments de Gsont d’ordre 2
donc G'C2×C2.
4

Exercice 7 On considère l’extension l’extension Q⊂Q(j, 3
√2) et on pose G=Gal(Q(j, 3 √2) : Q). Soit
θ∈G.
1) Quelles sont les valeurs possibles de θ(3
√2) ?
Solution: θ(3
√2) est racine de X3−2ainsi θ(3 √2) = 3 √2, j 3 √2ou j23 √2.
2) Quelles sont les valeurs possibles de θ(j)?
Solution: θ(j)est racine de 1 + X+X2ainsi θ(j) = jou j2.
3) Déterminer G.
Solution: D’après les questions précédentes, on voit que |G|= 6. En effet chaque choix de valeur
pour (θ(3
√2), θ(i)) définit un élément de G. Les éléments de Gsont donc
θ1:α7−→ α θ4:α7−→ α
j7−→ j j 7−→ j2
θ2:α7−→ jα θ5:α7−→ jα
j7−→ j j 7−→ j2
θ3:α7−→ j2α θ6:α7−→ j2α
j7−→ j j 7−→ j2
où α=3
√2. Reste à déterminer si G'C6ou G'S3. On remarque θ2◦θ4(α) = jα et θ4◦θ2(α) = j2α.
Le groupe Gn’est donc pas abélien, on a G'S3. Une manière plus explicite de voir cela est de
regarder l’action de Gsur les racines du polynôme X3−2:
θ1:α7−→ α θ4:α7−→ α
jα 7−→ j jα 7−→ j2α
j2α7−→ j2α j2α7−→ jα
θ2:α7−→ jα θ5:α7−→ jα
jα 7−→ j2α jα 7−→ α
j2α7−→ α j2α7−→ j2α
θ3:α7−→ j2α θ6:α7−→ j2α
jα 7−→ α jα 7−→ jα
j2α7−→ jα j2α7−→ jα
On voit par exemple que θ2est un cycle de longueur 3.
5