Télécharger

Devoir de 2h 5/02/2010 Physique appliquée
Exercice n°1 :
On se propose d'étudier quelques éléments constitutifs d'un scooter électrique.Le scooter
fonctionne grâce à un moteur à courant continu à excitation séparée et constante. Il est
alimenté par une source d'énergie embarquée constituée de batteries cadmium-nickel.
Elles sont rechargeables à partir du secteur par l'intermédiaire d'un transformateur et d'un
redresseur.
La vitesse du scooter est réglable par un hacheur.
Dans tout le problème on supposera que la vitesse v du scooter exprimée en km.h-1 est
proportionnelle à la fréquence de rotation n du moteur en tr.min-1.
Pour n= 1000 tr.min-1 le scooter roule à 50 km.h-1.
PARTIE 1 : ÉTUDE DU MOTEUR
A. Étude du moteur à tension d'induit U constante :
Le moteur fonctionne sous tension d'induit nominale : UN = 20V.
L'intensité nominale du courant d'induit : IN = 100A.
Tension d'excitation constante Ue = 18V.
L'intensité du courant d'excitation constante : Ie = 1,5A.
La résistance de l'induit R= 0,050 Ω.
Régime nominal: nN = 1000 tr.min-1 le scooter roule alors à 50 km.h-1.
A.1. Compléter le schéma électrique de ce moteur sur le document réponse 1 avec les
indications jointes au schéma.
Le courant d'induit étant positif, orienter les conducteurs.
A.2. Montrer que la f.é.m. E du moteur est proportionnelle à la fréquence de rotation n en
Bernaud J. 1/6

Devoir de 2h 5/02/2010 Physique appliquée
tr.min-1: E = k.n.
Calculer E. En déduire la valeur du coefficient de proportionnalité k et préciser son unité.
A.3. Montrer que lorsque I = IN = 100A, la fréquence de rotation n (en tr.min-1) et la
tension d'alimentation U (en volts) sont liées par la relation : n = 67.U - 330.
A.4. Montrer que le moment du couple électromagnétique Tem est proportionnel à
l'intensité du courant absorbé par l'induit : Tem = k'.I. Calculer Tem pour le
fonctionnement nominal. Calculer la valeur du coefficient de proportionnalité k' et préciser
son unité.
A.5. Montrer que l'expression liant le moment du couple électromagnétique Tem à la
fréquence de rotation n (en tr.min-1) et à la tension d'induit U (en V) peut se mettre sous
la forme : Tem = 2,80.U - 0,042.n
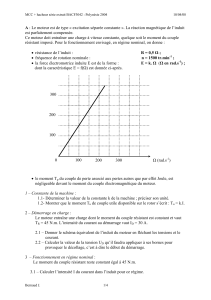
A.6. Pour U = UN = 20 V, déterminer l'équation de la caractéristique Tem = f(n).
Tracer cette caractéristique sur le document réponse 2.
A.7. Calculer les pertes par effet Joule totales de ce moteur pour I = IN.
A.8. Compléter le schéma du bilan de puissances, document réponse 1, de ce moteur
en précisant les expressions littérales des puissances au régime nominal.
A.9. Pour le fonctionnement nominal, la somme des pertes dans le fer et des pertes
mécaniques vaut pc = 100W. Déterminer le rendement.
B. Étude du moteur sous tension d'induit U réduite
Le conducteur du scooter dispose d'un mode de conduite économique. La tension
d'induit du moteur est alors : Ueco = 13 V.
B.1. Pour U = Ueco = 13 V déterminer l'équation de la caractéristique Tem = f(n). Tracer
cette caractéristique sur le document réponse 2.
B.2. Pour un moment du couple électromagnétique développé Tem = 17 N.m, déterminer
o la vitesse de rotation du moteur neco en tr min-1;
o la vitesse du scooter veco en km.h-1.
Bernaud J. 2/6

Devoir de 2h 5/02/2010 Physique appliquée
Dispositif de contrôle de charge de la batterie.
Le schéma du dispositif est sur le document réponse n°3.
La tension E0 provient de l'ensemble des trois batteries. Un relais ouvre le circuit de
charge de la batterie lorsque la tension à ses bornes atteint 20 V.
L'amplificateur opérationnel est parfait et ses tensions de polarisation sont :
Vsat- = 0V et Vsat+ = 15 V. Le transistor est alimenté sous Vcc = 24V
R0= 10 kΩ; R1= 14 kΩ.
B.1 Quel est le mode de fonctionnement de l'amplificateur opérationnel ?
B.2 Flécher la tension différentielle notée vd = (V+-V-) sur le schéma.
B.3 Quel doit être l'état du transistor T pendant la charge de la batterie ?
B.4 Quelle est la valeur de la tension Us pendant la charge ?
B.5 Quelle doit être alors le signe de vd ?
B.6 Quelle est la valeur de la tension V- appliquée à l'entrée inverseuse de
l'amplificateur opérationnel au moment où la charge est coupée? Quelle doit être la valeur
de V+ ?
B.7 Sachant que R1 = 14 kΩ, calculer la valeur à donner à R2 pour que la charge de la
batterie s'arrête dès que E0= 20 V.
Bernaud J. 3/6

Devoir de 2h 5/02/2010 Physique appliquée
Bernaud J. 4/6

Devoir de 2h 5/02/2010 Physique appliquée
Exercice n°2
Le réseau électrique fourni par EDF est un réseau triphasé 11,5 kV / 20 kV ; 50 Hz.
Afin de vérifier le réseau de tensions, nous avons placé un oscilloscope et deux sondes
différentielles de rapport 1/1000 entre la phase 1 et le neutre et entre la phase 2 et le neutre.
On a obtenu l'oscillogramme suivant, figure 1 :
Bernaud J. 5/6