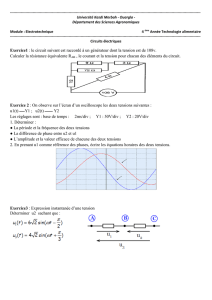
Groupement de montages redresseurs

Association de redresseurs Page 1 sur 11 TS2 ET 2006-2007
Groupement de montages redresseurs
Il s’agit d’améliorer les performances d’un redresseur seul vis-à-vis de la charge, du réseau ou bien des deux.
On peut associer des redresseurs commandés ou non commandés, en série ou parallèle.
I. Association de deux redresseurs P3 non commandés (tensions « faibles » et intensités « élevées »)
Ce montage, représenté ci-contre,
est connu sous le nom de « double
étoile ».
Intérêts :
- une seule diode dans le circuit à
chaque instant : la chute de tension
est limitée.
- meilleur forme de tension que le
P3 seul puisque l’indice
d’ondulation est de 6 au lieu de 3.
i
p1
v
'
1
v'
2
v'
3
u
c
v
3
v
2
v
1
D'
1
D'
2
D'
3
D
1
D
3
D
2
I
c
i
1
i
2
LL
- meilleur facteur de puissance que le P6.
1. Fonctionnement
Hypothèses :
- le courant continu est supposé parfaitement lissé,
i
1
(t) et i
2
(t) sont ininterrompus (ils ne s’annulent
jamais).
- les diodes, le transformateur et la bobine à point
milieu sont supposés parfaits.
A chaque instant : I
c
= i
1
(t) + i
2
(t)
Si v
1
(t) est la plus grande des tensions parmi v
1
(t),
v
2
(t), v
3
(t) : D
1
est passante :
0
d
)(d
)()(
2
1
=−−
t
ti
Ltutv
c
Si v’
2
(t) est la plus grande des tensions parmi v’
1
(t),
v’
2
(t), v’
3
(t) : D’
2
est passante :
0
d
)(d
)()('
1
c2
=−−
t
ti
Ltutv
En additionnant les deux équations :
0)
d
)(d
d
)(d
()(2)(')(
21
c21
=+−−+
t
ti
t
ti
Ltutvtv or
0
d
)(d
d
)(d
21
=+
t
ti
t
ti si le courant est parfaitement
lissé d’où
2
)()(
)(
21
c
tvtv
tu
−
=.
2. Etude des tensions
a. Indiquer les intervalles de conduction des
diodes.
Les deux redresseurs P3 (l’un constitué de D
1
, D
2
,
D
3
et l’autre de D’
1
, D’
2
, D’
3
) fonctionnent
indépendamment : on applique pour chacun les
règles des commutateurs à cathodes communes.
D
1
est passante lorsque v
1
(t) est la plus grande parmi v
1
(t), v
2
(t), v
3
(t) et ainsi de suite…
D’
1
est passante lorsque v’
1
(t) est la plus grande parmi v’
1
(t), v’
2
(t), v’
3
(t) et ainsi de suite…

Association de redresseurs Page 2 sur 11 TS2 ET 2006-2007
b. Représenter la tension aux bornes de la charge, calculer sa valeur moyenne et sa fréquence.
La loi des mailles appliquée sur la maille en
rouge donne : -u
c1
+ u
L1
+ u
c
= 0. L’intensité
i
1
étant périodique, la valeur moyenne de
u
L1
est nulle donc
c c1
3 2 3
V
u u= = π. La
valeur moyenne est égale à celle d’un P3 ce
qui était prévisible car il s’agit de deux P3
en parallèle.
LLLLLLL
D'
1
D'
2
D'
3
v
'
1
v'
2
v'
3
L
i
1
I
c
u
c
i
2
Lv
3
v
2
v
1
D
1
D
2
D
3
i
p1
u
c1
u
L1
Il y a six périodes de la tension redressée sur une période du réseau : la fréquence de la tension redressée est
de 300 Hz si celle du réseau vaut 50 Hz : c’est le double de la fréquence de la tension redressée en sortie
d’un P3 donc le filtrage est plus facile.
c. Représenter la tension aux bornes d’une diode.
On s’intéresse à la diode D
1
(voir l’orientation de v
D1
sur le
schéma ci-contre)
- lorsque D
1
est passante, la tension à ses bornes est nulle : v
D1
= 0
- lorsque D
2
est passante, l’application e la loi des mailles sur la
maille en rouge permet d’écrire : v
1
–v
D1
- v
2
= 0 soit v
D1
= u
12
.
Cette maille est intéressante car la tension aux bornes de D
2
est
nulle dans cette situation.
- lorsque D
3
est passante, l’application e la loi des mailles sur la
maille en bleu permet d’écrire : v
1
–v
D1
- v
3
= 0 soit v
D1
= u
13
. Cette
maille est intéressante car la tension aux bornes de D
3
est alors nulle.
LLLLLLL
L
I
c
u
c
i
2
Lv
3
v
2
v
1
v
D1
D
2
D
3
3. Etude des courants
a. Représenter les courants dans les diodes D
1
et D’
1
.
La diode D
1
est passante de
6
π
à
5
6
π
elle alors parcourue par la moitié du courant circulant dans la charge
soit
c
D1
2
I
i
=
. Elle est bloquée le reste du temps, on a alors
D1
0
i
=
.
La diode D’1 est passante de
7
6
π
à
11
6
π
elle alors parcourue par la moitié du courant circulant dans la charge
soit
c
D2
2
I
i
=
. Elle est bloquée le reste du temps, on a alors
D2
0
i
=
.
b. Représenter le courant ip1.
Les enroulements parcourus par ip1, iD1 et iD’1 sont bobinés sur la même colonne de transformateur. D’après la
loi de compensation des ampère tours :
1 p1 2 D1 2 D'1
n i n i n i
= − (pour les signes, se référer aux têtes
d’enroulement).
De
6
π
à
5
6
π
:
c
2
p1 1
2
I
n
in =
et de
7
6
π
à
11
6
π
:
c
2
p1 1
2
I
n
in = −
c. Calculer le facteur de puissance au primaire et comparer avec celui d’un redresseur P6.
c
c
p p
3
u I
P
k
S V I
= = avec V
p
et I
p
les valeurs efficaces des tensions simples et intensités en ligne au primaire.
1
p2
n
V V
n
= car V est la valeur efficace des tensions aux bornes des enroulements secondaires.

Association de redresseurs Page 3 sur 11 TS2 ET 2006-2007
Calcul de la valeur efficace I
p
de l’intensité en ligne au primaire :
2
c c2 2
p1 1
5 2
( ) .( )
2 6 6 2 3
I I
n n
In n
π π
= − =
Finalement
c
c
1 2
2 1
3 2 3
3
22
32 3
VI
kI
n n
V
n n
π
= =
π
. C’est la même valeur que le PD3.
Ce montage est intéressant car il divise par deux les chutes de tension aux bornes des diodes par rapport au
PD3, il est utilisé pour les charges demandant des courants élevés sous des tensions faibles.
Remarque : si l’intensité n’est pas suffisamment importante, les courant i
1
(t) et i
2
(t) peuvent s’annuler, on
retrouve le fonctionnement du P6.
II. Association série d’un PD3 et S3 non commandés (diminution de l’ondulation et amélioration du
facteur de puissance)
Intérêts :
- l’indice d’ondulation est égal à 12 alors que pour
le PD3 et le S3, il est égal à 6.
- le facteur de puissance de chaque secondaire est
meilleur que celui d’un redresseur seul ayant un
indice d’ondulation égal à 12.
1. Fonctionnement
La mise en série impose que la valeur moyenne de
la tension en sortie de chacun des ponts soit
identique, en déduire la relation entre les nombres
de spires des enroulements du secondaire en
triangle et des enroulements du secondaire en
étoile.
u
c1
u
c2
u
c
I
c
Y
y
d
a
1
c
1
b
1
c
2
b
2
a
2
A
B
C
Les valeurs moyennes des tensions de sortie de chaque pont sont données par reliées aux valeurs efficaces
des tensions aux bornes des enroulements par :
PD3 (pont du haut) :
y
c1
3 2 3
V
u=π V
y
est la valeur efficace de la tension aux bornes
d’un enroulement secondaire.
S3 (pont du bas) :
d
c2
3 2
V
u=
π
V
d
est la valeur efficace de la tension aux bornes
d’un enroulement secondaire.
Relation des tensions pour les transformateurs « colonnes » :
y 2y
1
V n
V n
= et
d 2d
1
V n
V n
= avec n
2y
et n
2d
les
nombres de spires pour les secondaires en étoile et en triangle et V la valeur efficace des tensions simples au
primaire.
Les valeurs moyennes des tensions redressées deviennent
2y
1
c1
3 2 3
nV
n
u=π et
2d
1
c2
3 2
nV
n
u=π. Leur
égalité conduit à la relation
2y 2d
1 1
3 2 3 3 2
nn
V V
n n
=
π π soit
2y 2d
3
n n
=

Association de redresseurs Page 4 sur 11 TS2 ET 2006-2007
2. Etude des tensions
Le schéma ci-contre représente les enroulements primaires et
secondaires du transformateur. Les traits pointillés indiquent que
les enroulements sont placés sur la même colonne du circuit
magnétique (il en est de même pour B, b
1
, b
2
et C, c
1
, c
2
).
Les graphes de la page suivante représentent les tensions secondaires
du transformateur. Celles représentées en gras sont en phase avec les
tensions primaires (v
1
avec v
A
, v
2
avec v
B
et v
3
avec v
C
).
a. Repérer ces tensions.
v
a1
est en phase avec v
1
donc u
a1b1
est en avance de 30° sur v
1
. u
a2c2
est en phase avec v
1
.
v
A
v
B
v
C
A
B
C
a
1
b
1
c
1
a
2
b
2
c
2
b. Indiquer les intervalles de conduction des diodes (voir le document réponse)
Pour le PD3 :
Commutateur à cathodes communes : la diode passante est celle dont l’anode est reliée à la tension la plus
grande. L’anode de la diode D
1
est reliée à v
a1
(qui est en phase avec v
1
), donc D
1
est passante lorsque v
1
est
plus grande que v
2
et v
3
.
Commutateur à anodes communes : la diode passante est celle dont la cathode est reliée à la tension la plus
petite. La cathode de la diode D
4
est reliée à v
a1
(qui est en phase avec v
1
), donc D
4
est passante lorsque v
1
est
plus petite que v
2
et v
3
.
Pour le S3 :
Commutateur à cathodes communes : la diode passante est celle dont l’anode est reliée à l’enroulement dont
la tension est devenue positive la dernière. L’anode de la diode D’
1
est reliée à u
a2c2
(qui est en phase avec
v
1
), donc D
1
devient passante lorsque v
1
devient positive et se bloque lorsque v
2
devient positive (c’est la
diode D’
2
reliée à u
b2a2
qui devient passante).
Commutateur à anodes communes : la diode passante est celle dont la cathode est reliée à l’enroulement dont
la tension est devenue négative la dernière. La cathode de la diode D’
4
est reliée à u
a2c2
(qui est en phase avec
v
1
), donc D’
4
devient passante lorsque v
1
devient négative et se bloque lorsque v
2
devient négative (c’est la
diode D’
5
reliée à u
b2a2
qui devient passante).
c. Représenter les tensions u
c1
(t) et u
c2
(t). En déduire la tension u
c
(t). Quelle est sa fréquence ?
Pour le PD3 :
- Lorsque D
1
et D
5
sont passantes alors u
c1
= v
a1
– v
b1
soit u
a1b1
, cette tension est en avance de 30° sur v
1
(voir graphique).
- Lorsque D
1
et D
6
sont passantes alors u
c1
= v
a1
– v
c1
soit u
a1c1
, cette tension est en retard de 30° sur v
1
(voir graphique).
0
v
1
(t)
u
a1c1
(t)u
a1c1
(t)
u
c1
(t)
t
Pour le S3 :
- Lorsque D’
1
et D’
5
sont passantes alors
u
c2
= – u
b2a2
, cette tension est en opposition de
phase avec v
2
(voir graphique).
- Lorsque D’
1
et D’
6
sont passantes alors u
c2
= u
a2c2
qui est en phase avec v
1
(voir graphique).
0
v
1
(t)
u
b2a2
(t)
u
c2
(t)
t
-u
b2a2
(t)
La tension u
c
(t) est obtenue en faisant la somme des tensions u
c1
(t) et u
c2
(t) (représentation page suivante).

Association de redresseurs Page 5 sur 11 TS2 ET 2006-2007
d. Calculer la valeur moyenne de la tension de sortie.
Les tensions composées au primaire ont pour valeur
efficace 20 kV. Un enroulement primaire comporte
200 spires, un enroulement du secondaire couplé en
triangle comporte 40 spires.
Les deux redresseurs sont en série, la valeur moyenne
de u
c
est égale à deux fois celle de u
c2
(ou deux fois
celle de u
c2
).
23
1
c c2
3 2 6 2 40 20.10
2. 2. . . 6240
200 3
d
nV
n
u u= = = =
π π V
car la valeur efficace des tensions simples primaires
est égale à
3
20.10
3
.
0
v
1
(t)
u
c2
(t)
t
u
c1
(t)
u
c
(t)
3. Etude des courants
Représenter le courant dans un enroulement primaire du transformateur puis calculer le facteur de puissance
primaire.
La loi de compensation des ampères tours permet d’écrire :
2d a2 2y a1 1 A
n i n i n i
+ = soit
2y
2d
A a2 a1
1 1
n
n
i i i
n n
= +
Rappels sur les intensités i
a1
et i
a2
(voir aussi le cours sur
les redresseurs à diodes).
Pour i
a1
:
Sur
0,
6
π
,
5 7
,
6 6
π π
et 11
,2
6π
π
: i
a1
= 0
v
A
A
B
C
v
B
v
C
a
1
b
1
c
1
a
2
b
2
c
2
i
A
i
a1
i
a2
De
6
π
à
5
6
π
:
a1 c
i I
=
et de
7
6
π
à
11
6
π
:
a1 c
i I
= −
Pour i
a2
:
Sur
0,
3
π
, 2
,
3
π
π
:
a2 c
1
3
i I
= ; sur
2
,
3 3
π π
:
a2 c
2
3
i I
=
Sur
4
,
3
π
π , 5
,2
3
π
π
:
a2 c
1
3
i I
= − ; sur
4 5
,
3 3
π π
:
a2 c
2
3
i I
= −
Entre 0 et π le courant i
A
est constitué de trois paliers dont les valeurs sont :
Palier inférieur (entre 0 et
6
π
) :
2d c
A1
3
n I
in =
Palier intermédiaire (entre
6
π
et
3
π
) :
2y
2d c 2d c 2d
A c c
1 1 1 1
3 3 3.
n
n I n I n
i I I
n n n
n
= + = +
Palier supérieur (entre
3
π
et
2
π
) : 2d c 2d
A c
11
233. n I n
i I
n
n
= +
On retrouve les mêmes valeurs absolues pour l’intervalle [π, 2π].
Valeur efficace :
2 2 2
2d c 2d c 2d 2d c 2d
eff c c
1 1 1
1 1
2
4
( ) ( ) ( )
2 6 3 6 3 6 3
3. 3.
n I n I n n I n
I I I
n n n
n n
π π π
= + + + +
π