CHAPITRE 12 : BISSECTRICE Objectifs Connaître et utiliser la

CHAPITRE 12 : BISSECTRICE
Objectifs
Connaître et utiliser la définition de la bissectrice.
TD n°1p77
Utiliser différentes méthodes pour tracer la bissectrice d’un angle.
TD n°2p71
Caractériser les points de la bissectrice d’un angle donnée par la propriété
d’équidistance aux deux côtés de l’angle.
TD n°4 et 5p77
Construire le cercle inscrit dans un triangle.
TD n°1p78
I. Bissectrice
1. Définition
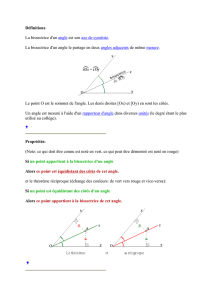
Définition : La bissectrice d’un angle est la demi-droite qui partage cet angle en deux angles adjacents
de même mesure.
Bissectrice de l’angle 
2. Propriétés
Propriété (admise) : Si un point appartient à la bissectrice d’un angle, alors il est équidistant des deux
côtés de cet angle.
Exemple :
Donnée : F appartient à la bissectrice de l’angle 
.
Conclusion : F est équidistant des deux côtés de l’angle. (GF = FH)
Propriété (admise) : Si un point est équidistant des côtés d’un angle, alors il appartient à la bissectrice
de cet angle.
Exemple :
Donnée : F est équidistant des deux côtés de l’angle.
(GF = FH)
Conclusion : F appartient à la bissectrice de l’angle 
.

II. Cercle inscrit
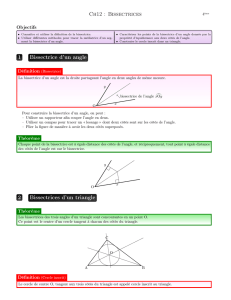
Définition : Le cercle inscrit dans un triangle est le cercle tangent aux trois côtés de ce triangle.
Propriété : Les bissectrices des angles d’un triangle sont concourantes en un point qui est le centre du
cercle inscrit dans ce triangle.
Exemple :
Démonstration :
Soit ABC un triangle, tel que les bissectrices des angles 
 et   s’intersectent au point I.
On sait que I appartient à la bissectrice 
.
Or, si un point appartient à la bissectrice d’un angle, alors il est équidistant des deux côtés de cet
angle.
Donc I est équidistant des côtés [BA] et [BC].
On sait que I appartient à la bissectrice 
.
Or, si un point appartient à la bissectrice d’un angle, alors il est équidistant des deux côtés de cet
angle.
Donc I est équidistant des côtés [CB] et [CA].
Comme I est équidistant des côtés [BA] et [BC] et des côtés [CB] et [CA], alors il est équidistant des
côtés [BA] et [CA].
On sait que I est équidistant des côtés [AB] et [AC].
Or, si un point est équidistant des côtés d’un angle, alors il appartient à la bissectrice de cet angle.
Donc I appartient à la bissectrice de l’angle 
.
Donc I est le point d’intersection des trois bissectrices du triangle ABC.