Term S - Site Gerald VINCENT

ds2tr3ts20112012 Devoir de Sciences-Physiques n°2 (2h) Mardi 30 mars 2012
CHIMIE LA PILE CUIVRE-ALUMINIUM ( points)
Données :
Quantité d’électricité transportée par une mole d’électrons : F = 9,6510 4 C.mol – 1
Masse molaire de l'aluminium: 27 g.mol-1
On introduit dans un becher un volume V = 50 mL d'une solution de chlorure d'aluminium
(Al3+ + 3 Cl–), de concentration en soluté apporté 0,10 mol.L-1, dans laquelle plonge une lame
d'aluminium. Dans un second bécher, on introduit un volume V = 50 mL d'une solution de
sulfate de cuivre (Cu2+ + SO42–), de concentration molaire en soluté apporté 0,10 mol.L-1,
dans laquelle plonge une lame de cuivre. On relie les deux béchers à l'aide d'un pont salin
contenant du nitrate d'ammonium (NH4+ + NO3–).
Lorsqu'on branche un voltmètre électronique avec sa borne COM reliée à l'électrode
d'aluminium, on mesure une différence de potentiel U = + 1,8 V.
1. Quelle est la polarité de la pile ?
2. Quel est le rôle du pont salin ?
3. On relie la pile à un conducteur ohmique de résistance R.
a- Faire un schéma légendé de la pile et du circuit extérieur en indiquant le sens du
courant dans le circuit, et en représentant le déplacement des différents porteurs
de charge à l'intérieur et à l'extérieur de la pile.
b- Écrire et nommer les réactions qui se produisent aux électrodes en précisant
celles-ci.
c- En déduire l’équation de la réaction se produisant dans la pile.
d- Calculer le quotient de réaction initial Qri associée à cette transformation.
e- La constante d'équilibre associée à cette transformation étant égale à K = 1020
montrer que le sens d'évolution est cohérent avec le fonctionnement de la pile.
f- On considère que la pile débite une intensité constante I = 40 mA au cours de son
fonctionnement.
- Quel réactif peut-on considéré comme limitant ? Justifier.
- En déduire la capacité Qmax de cette pile c’est à dire la quantité maximale
d’électricité qu’elle peut fournir (on trouve Qmax = 965 C).
- Dans ces conditions, quelle sera la durée de vie Δt de cette pile ?
g- La pile fonctionne pendant 1 h 30 min en débitant un courant d'intensité constante
I = 40 mA. Calculer la perte de masse de l'électrode d'aluminium.

PHYSIQUE ( points )
Exercice 1 : – LA GRÊLE ( points )
La grêle se forme dans les cumulo-nimbus situés entre 1000 m et 10000 m d’altitude où la
température est très basse, jusqu’à – 40 °C. Le grêlon tombe lorsqu’il n’est plus maintenu au
sein du nuage. Au sol sa vitesse peut atteindre 160 km/h.
On étudie un grêlon de masse 13 g qui tombe d’un point O d’altitude 1500 m sans
vitesse initiale. Il peut être assimilé à une sphère de diamètre 3,0 cm.
Le point O sera pris comme origine d’un axe Oz orienté positivement vers le bas. L’intensité
de la pesanteur sera considérée comme constante et de valeur g = 9,80 m.s-2.
Données : volume d’une sphère V =
3
3
4r
; masse volumique de l’air  = 1,3 kg.m-3
A – CHUTE LIBRE (NE PAS REPONDRE à CETTE PARTIE A !!)
On admettra que le grêlon tombe en chute libre.
1. En appliquant la deuxième loi de Newton, déterminer les équations horaires donnant
la vitesse et la position du centre d’inertie G du grêlon en fonction de la durée t de
la chute.
2. Calculer la valeur de la vitesse lorsqu’il atteint le sol, ce résultat est-il
vraisemblable ? Justifier.
B – CHUTE REELLE
En réalité le grêlon est soumis à deux autres forces, la poussée d’Archimède
A
F
et la force
de frottement fluide
F
proportionnelle au carré de la vitesse telle que F = K×v².
1. Donner l’expression de la valeur de la poussée d’Archimède ; la calculer et la
comparer à celle du poids..
2. On néglige la poussée d’Archimède.
a) Établir l’équation différentielle du mouvement.
Montrer qu’elle peut s’écrire sous la forme
2
B.vA
dt
dv 
et donner l’expression
des constantes A et B.
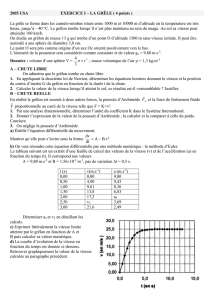
b) On veut résoudre cette équation
différentielle par une méthode d’Euler.
Le tableau ci-contre est un extrait
d’une feuille de calcul des valeurs de la
vitesse (v) et de l’accélération (a) en
fonction du temps (t).
Il correspond aux valeurs
A = 9,80 m.s-2 et B = 1,5610-2 m-1,
- Quelle est la valeur du pas
d’itération t ?
- Etablir les expressions de l’accélération ai et de la vitesse vi+1 par la
méthode d’Euler.
t (s)
v(m.s-1)
a (m.s-2)
0,00
0,00
a0
0,50
4,90
9,43
1,00
9,61
8,36
1,50
13,8
6,83
2,00
17,2
a4
2,50
v5
3,69
3,00
21,6
2,49

- Que vaut l’accélération initiale a0 ?
- Déterminer a4 et v5
en détaillant les
calculs.
c) Exprimer littéralement la
vitesse limite atteinte
par le grêlon en fonction
de A et B puis calculer sa
valeur numérique.
d) La courbe d’évolution de la
vitesse en fonction du
temps est donnée ci-
contre. Retrouver
graphiquement la valeur
de la vitesse calculée à la question précédente.
Exercice 2 : Réalisation artisanale d'un diapason électronique ( points)
Un groupe d'élèves musiciens souhaite réaliser un diapason électronique capable d'émettre
des sons purs, en particulier la note la3 (note la du troisième octave). Cette note sert de
référence aux musiciens pour accorder leurs instruments.
Un son pur est une onde acoustique sinusoïdale de fréquence donnée. Il peut être obtenu
par excitation d'un haut-parleur à l'aide d'une tension électrique sinusoïdale de même
fréquence.
Le circuit électrique qui permet d'obtenir une tension sinusoïdale est constitué d'une
bobine, d'un condensateur et d'une résistance (voir annexe à rendre avec la copie).
Les élèves vont réaliser les différentes étapes du circuit oscillant permettant d'émettre
les sons de la gamme tempérée (gamme musicale élaborée par J.S. Bach et couramment
utilisée en Occident).
Ils étudieront :
l'établissement des oscillations électriques.
l'influence des paramètres du circuit leur permettant d'obtenir la note
souhaitée.
DOCUMENT : octave 3 de la gamme tempérée
Note
do
ré
mi
fa
sol
la
si
Fréquence
(en Hz)
262
294
330
349
392
440
494

1. Réalisation d'oscillations électriques
Le condensateur C est chargé sous la tension E du générateur ; on bascule ensuite
l'interrupteur K en position 2. Cet instant est choisi comme origine des temps.
1.1. La tension u aux bornes du condensateur évolue en fonction du temps de la manière
présentée en annexe (à rendre avec la copie).
a. Noter sur le schéma de l’annexe (à rendre avec la copie) la flèche de tension u
visualisée (convention récepteur).
b. Noter sur le schéma de l’annexe (à rendre avec la copie) les branchements de
l’interface d’acquisition permettant la visualisation de la tension u
c. Les oscillations électriques observées sont amorties.
Quel est le dipôle responsable de cet amortissement ?
d. Qualifier ce régime d'oscillations par un terme approprié.
1.2. Sur la courbe u = f(t) présentée en annexe (à rendre avec la copie), sont notés
deux points C et D. Comment appelle-t-on la durée écoulée entre ces deux points ?
Évaluer graphiquement cette valeur : la « dessiner » sur la courbe.
2. Entretien des oscillations
En feuilletant leur manuel de physique, les élèves constatent qu'il est possible de rajouter
au circuit précédent, un dispositif qui entretient les oscillations.
2.1. Expliquer, en une phrase, le rôle de ce dispositif, d'un point de vue énergétique.
2.2. Sachant que les paramètres du circuit précédent n'ont pas été modifiés,
représenter, sur l'annexe (à rendre avec la copie), la courbe u = f(t) obtenue après
entretien des oscillations.
2.3. Rappeler l'expression de la période propre T0 du circuit oscillant. Calculer sa valeur,
sachant que le condensateur a une capacité C = 1,0 µF et que l'inductance L de la bobine
vaut ici 0,100 H.
2.4. En déduire la fréquence f0 de la tension obtenue.
2.5. Le circuit oscillant est relié à un haut-parleur convertissant cette onde électrique en
onde sonore de fréquence f0. Les élèves souhaitent accorder leurs instruments en
émettant la note la3 à l'aide du circuit précédent.
a- La fréquence précédemment obtenue est-elle un son de l'octave 3 de la gamme ?
b- Quels paramètres peut-on changer pour modifier la valeur de la fréquence émise ?
c- Sachant que les élèves ne disposent pas d'autre condensateur que celui du circuit
initial, calculer la valeur de l'autre paramètre qui permettra d'obtenir la note la3 .

NOM PRENOM
ANNEXE : à rendre avec la copie
Exercice 2 : diapason électronique
G : Générateur de tension constante
E = 12 V
R : Résistance du conducteur
ohmique
R = 1000 Ω
C : Capacité du condensateur
C = 1,0 µF
L : Inductance réglable de la bobine
(résistance r négligeable)