DEVOIR N°4 [CCP PSI 1999 sauf Q18 à Q21 (ESIM PC 1997) et

Spé ψ 2002-2003 page 1/6 devoir n°4 corrigé
DEVOIR N°4
[CCP PSI 1999 sauf Q18 à Q21 (ESIM PC 1997) et Q39 à Q46 (CENTRALE PSI 2000)]
ÉLABORATION ET USAGES DU CUIVRE
PARTIE I
Q1: Les applications du cuivre proviennent de sa conductivité électrique élevée, sa malléabilité, sa
résistance à la corrosion et son aptitude au soudage. Il est donc utilisé comme conducteur électrique
(production, transformation, transport et utilisation de l’électricité), dans les canalisations (eau et
gaz), hélices de bateaux, toitures de bâtiments, …. Il se rencontre également dans de nombreux al-
liages (laitons, bronzes, …).
Q2: Le fer (7×108 tonnes.an—1) et l’aluminium (1,5×107 tonnes.an—1) sont produits en plus grande
quantité que le cuivre (7×106 tonnes.an—1).
Q3 : Le nombre d’atome appartenant à la maille est 8×1/8 + 6×1/2 = 4 atomes.
Q4 : On a ρ =
m
V
M
a
=
4
3
N. A.N.
( )
3
1223
3
10.5,36110.023,6
10.5,63.4
−
−
=ρ = 8,92×
10
3
+
kg.m—3.
PARTIE II
Q5 : Cu2S: no(S) = —II; no(Cu) = +I; CuS: no(S) = —II; no(Cu) = +II;
Cu2O: no(O) = —II; no(Cu) = +I; CuO: no(O) = —II; no(Cu) = +II;
CuFeS2: no(S) = —II donc no(Cu) + no(Fe) = +IV ce qui autorise deux possibilités:
no(Fe) = +III et no(Cu) = +I ou bien no(Fe) = +II et no(Cu) = +II;
Cu2(OH)2CO3: charge de OH: —1; charge de CO3: —2 donc no(Cu) = +II.
Q6 : On constate que l’état du cuivre ne peut pas être déterminé dans le cas de la chalcopyrite
CuFeS2.
Q7 : Le bilan indiqué est celui de l’oxydation de la chalcopyrite par le dioxygène. Dans SO2, le sou-
fre est à l’état +IV. Il est à l’état –II dans CuFeS2.
On peut envisager les variations d’états d’oxydation suivantes :
Les deux électrons restant à enlever peuvent l’être de 2 Fe(+III) passant à 2 Fe(+II) ou de 2 Cu(+II)
passsant à 2 Cu(+I). Cela ne lève donc pas l’ambiguité. On peut cependant présumer que la réduc-
tion des ions cuivriques est plus facile que celle des ions ferriques.
Q8 : Dans chaque atome de O2, l’élément oxygène est à l’état 0; il passe à
l’état —II dans SO2: il est donc réduit.
Il y a 4 atomes de soufre à l’état —II dans 2(CuFeS2). On en retrouve 3 dans
le même état dans Cu2S et 2(FeS). Mais l’atome présent dans SO2 est à l’état
+IV. Il a été oxydé.
Les deux atomes de l’élément Cu de 2(CuFeS2) passent de l’état +II à l’état
+I. L’élément Cu est donc réduit, ce qui met en jeu 2×1 = 2 électrons.
Q9 : S’il n’y avait pas d’ions Cu+, les ions O2— seraient en contact le long de
la diagonale du cube. En notant d la longueur de la demi-diagonale du cube,
2 CuFeS
2
4×(-II)
+ O
2
2
×
(0)
Cu
2
S
(-II)
+ 2
FeS
2
×
(-II)
+ SO
2
(+IV)
2×(–II)
2×(+I)
+VI
–IV
2×(+II)

Spé ψ 2002-2003 page 2/6 devoir n°4 corrigé
on a (2d)2 = 3.
a
Cu O
2
2 soit d = 3
2
2
aCu O. Numériquement, on trouve d = 369,8 pm or on donne pour le
rayon de l’ion O2— rO = 140 pm < d/2. On en conclut que les ions O2— ne sont pas en contact: la
structure n’est donc pas compacte.
Q10 : Le volume de la maille est V = aCu O
2
3. Les ions Cu+ et O2— étant en contact le long d’un quart
d’une diagonale du cube, on a
d
2
= rCu + rO donc rCu =
369
8
2
,
— 140 = 44,9 pm. Les 4 ions Cu+
appartiennent en propre à la maille mais on n’a que 8×1/8 + 1 = 2 ions O2— dans la maille (ce qui
est conforme à la stoechiométrie). Le volume total des atomes de la maille est donc VA-
TOME =
(
)
3
O
3
Cu r.2r.4
3
4+π . La compacité de la structure est alors
(
)
3OCu
3
O
3
Cu
2
a
r.2r.4
3
4
c+π =. Numérique-
ment on trouve c = 0,315.
Q11 : Chaque ion O2— possède 4 plus proches voisins cuivre. Il est au centre d’un tétraèdre dont
chaque sommet est occupé par un ion Cu+.
PARTIE III
Q12 : Les facteurs intensifs d’équilibre d’un système sont a priori la température T, la pression to-
tale pTOTAL et les fractions molaires des différentes espèces. Il n’y a qu’une seule espèce dans la
phase gazeuse (SO2) donc p(SO2) = pTOTAL et sa fraction molaire vaut 1. Les autres espèces sont
solides donc elles sont seules dans leur phase. Les facteurs d’équilibre du système sont donc la pres-
sion totale pTOTAL et la température T. Comme on observe que l’état d’équilibre du système avec
toutes les espèces présentes produit une pression totale déterminée par la température, il n’y a qu’un
seul facteur d’équilibre indépendant: la variance du système vaut donc 1.
Q13 : Le tableau montre que la pression de SO2 obtenue à l’équilibre augmente avec la température
du système. Donc une élévation de température favorise le sens direct du bilan. D’après la loi de
Van’t Hoff, ce sens (direct) est le sens endothermique.
Q14 : On sait que, en supposant ∆rH° et ∆rS° indépendants de la température (approximation
d’Ellingham), on a ∆rG°(T) = ∆rH°— T.∆rS°. D’autre part ∆rG°(T) = —RT ln K°(T) par définition de
K°(T). On peut donc écrire ln K°(T) =
−
°
+
°
∆
∆
r r
H
RT
S
R
. Comme la condition d’équilibre du système
s’écrit K°(T) =
p
p
EQ 2
(SO
)
0
, on trace la courbe de ln
p
p
EQ 2
(SO
)
0
en fonction de
1
T
. On a le tableau de
valeurs:
T (en K) 923 973 1023 1073
1/T (en K—1)1,08×10—3 1,03×10—3 0,98×10—3 0,93×10—3
p(SO2) (en bar) 0,33 0,66 1,23 2,16
ln 
0
2EQp
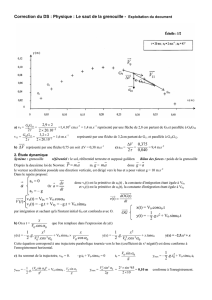
)SO(p —1,11 —0,42 0,21 0,77
On obtient la courbe suivante dont la pente est p = — 1,25×104; or
∆rH° = — p.R donc numériquement: on a
∆rH° = 104 kJ.mol—1.
L’ordonnée à l’origine est y0 = 12,39 et ∆rS° = y0.R donc numérique-
ment on a ∆rS° = 103 JK—1.mol—1
invt/10¬¼
990
1000
1010
1020
1030
1040
1050
1060
1070
lnp
-1
-0.8
-0.6
-0.4
-0.2
0

Spé ψ 2002-2003 page 3/6 devoir n°4 corrigé
Q15 : On peut écrire: ∆rS°= [S°(SO2) + 6×S°(Cu)] —[2×S°(Cu2S) + S°(Cu2O)].
La seule espèce gazeuse est SO2: son entropie standard est la plus élevée car elle présente le plus
grand nombre d’états microscopiques. A l’inverse, parmi les trois espèces solides, Cu possède
l’entropie standard la plus faible car il est constitué d’un seul type d’atomes. On a bien ∆rS° > 0.
Q16 : Avec les valeurs de ∆rH° et ∆rS° trouvées ci-dessus, on obtient, à T = 733°C,
∆rG° = 104-(1006)×103×10—3 = 0. La température Ti = 733°C est donc la température d’inversion
du système. Se placer à une température supérieure favorise le sens direct du bilan, c’est-à-dire la
production de cuivre. Cette considération thermodynamique s’accompagne sans doute aussi par une
augmentation de la vitesse de la réaction.
Q17 : La température 1083°C = 1356 K est la température de fusion du cuivre. En se plaçant à une
température supérieure, on obtient du cuivre à l’état liquide ce qui le rend plus facile à séparer des
autres réactifs et à couler en lingots.
Q18 : A l’anode se produit les oxydations. On peut envisager :
Cu(S) → (Cu2+)aq + 2 e– E = 0,34 V ;
3 H2O → ½ O2 + 2 H3O+ + 2 e— E = 1,23 V à pH = 0.
A la cathode se produit les réductions. On peut envisager :
(Cu2+)aq + 2 e— → Cu(S) E° = 0,34 V ;
2 H+ + 2 e— → H2(G) E = 0,0 V à pH = 0.
Q19 : On peut tracer l’allure des courbes intensité-potentiel : La réaction qui se produit à l’anode
est donc l’oxydation du cuivre
métal en Cu2+. L’anode se décom-
pose ce qui explique le terme
« anode soluble ».
A la cathode se produit la réduction
des Cu2 + en Cu(S).
En indiçant par A et C les espèces à
l’anode et à la cathode, le bilan d’électrolyse s’écrit :
CuA + Cu2+C = CuC + Cu2+A
Compte tenu des surtensions, la tension minimale d’électrolyse est 0,1 V.
Q20 : Pendant une durée τ circule la charge q = iτ soit la quantité d’électrons n
i
N e
i
eA
= =
τ
τ
F. Or
pour fabriquer une mole de Cu(S), il faut 2 moles d’électrons d’après la demi-équation redox. Pen-
dant τ, il est donc produit une masse de cuivre mCu = nCu.MCu =
i
τ
2
F
MCu. A.N.
mCu =
×
×
××−
3
20
60
2 96500 635 10 3
,= 1,18 g.
Q21 : On peut tracer ajouter sur le diagramme précédent l’allure des courbes intensité-
potentiel pour l’argent et le nickel, en tenant compte des surtensions.
V
i
1,73
0,34
0,24
–0,20
Cu(S) → Cu
2+
Cu(S) ← Cu
2+
H2O → O2(G)
H2(G) ← H
+
V
i
1,73
0,34
0,24
–0,20
Cu(S) → Cu
2+
Cu(S) ← Cu
2+
H2O → O2(G)
H2(G) ← H
+
Ag(S) → Ag
+
Ni
(S) → Ni
2+
Ni
(S) ← Ni
2+
0,90
–0,15
–0,65

Spé ψ 2002-2003 page 4/6 devoir n°4 corrigé
A l’anode, le cuivre est oxydé dès que le potentiel anodique dépasse 0,34 V : cela libère les impu-
retés nickel et argent. Si le potentiel ne dépasse pas 0,90 V, l’argent n’est pas oxydé et tombe au
fond de la cuve. Par contre, le potentiel est supérieur à –0,15 V donc le nickel est oxydé en Ni2+.
A la cathode, les ions Cu2+ sont réduits si le potentiel cathodique est inférieur à –0,15 V. Ils se trans-
forment en cuivre qui se dépose sur la cathode. Mais si le potentiel n’est pas inférieur à –0,65V, les
ions Ni2+ ne sont pas réduits et restent en solution. On a donc « dissolution » de l’anode de cuivre
impur et dépôt de cuivre pur à la cathode.
PARTIE IV
Q22 : La condition d’équilibre s’écrit K3
02
2
=+
+
[ ]
[ ]
Cu
H O
3
. Or sur le diagramme potentiel-pH, la frontière
entre les domaines de Cu2+ et CuO correspond au début de précipitation de CuO c’est-à-dire que
l’on a [Cu2+] = 1,0×10—2 mol.L—1. On lit qu’alors pH = 4,8 donc
( )
2
8,4
2
0
310
10.0,1
K−
−
= soit
K° = 3,98×107.
Q23 : La limite de précipitation d’une solution cuivrique de concentration 5 mol.L—1 correspond à
un pH tel que
[
], . H O
327
5
3 9810
+= d’où [H3O+] = 3,5.10—4 et pH = 3,4. Pour avoir une solution de
Cu2+ à 5 mol.L—1 entièrement dissous, il faut donc se placer à pH < 3,4.
Q24 : Notons C la concentration de l’acide sulfurique, on peut ne tenir compte que de la première
réaction qui est totale. On a alors h = C = 2 mol.L–1 d’où pH = 0,3 .
Q25 : La quantité de CuO introduite dans 1L de la solution est n(CuO) =
( ) 165,63 10.3,89 3 +
− = 1,12×10—3
mol. C’est donc le réactif limitant car on a initialement 2,02 mol de H
3
O
+
et la réaction ne
consomme pratiquement pas de H3O+.
Q26 : L’étape limitante est supposée du premier ordre par rapport à C donc on peut écrire
v
kC
=
.
Q27 : L’expression de la vitesse molaire spécifique de disparition de CuO est v
S
dn
dt
= − 1CuO
b
g
. Or
on a n(CuO) =
m
M
(
(
CuO)
CuO) =
N
m
MA CuO
.
b g où m est la masse d’une particule. En notant r le rayon de
cette particule, on a m =
4
3
3
π ρr. et S = 4πr2. L’expression de la vitesse devient
vrd
dt rN M
= −
F
H
G
I
K
J
1
44 3
23
ππρ
A
CuO
bg = −
N
M
dr
t
dt
A
CuO
(
)
ρ
b g . L’équation différentielle vérifiée par r(t) est
donc.dr t
dt kM NC
( ) CuO
A
= −
b
g
ρ d’après la loi cinétique.
Q28 : Comme on a vu que C reste pratiquement constant, on peut intégrer l’équation précédente en
r t r k M
NC t( ) ( ) CuO
A
= −0
b
g
ρ.
Q29 : Avec les données du tableau 2, on trace la courbe de r
en fonction de t. On obtient une droite ce qui confirme le
modèle précédent. La pente est p = —0,627 (pour r en µm

Spé ψ 2002-2003 page 5/6 devoir n°4 corrigé
et t en min). On en déduit k = 0 627 10
60 6 02 10 649 79 5 10 210
6 23
3 3
, ,, . × × ×
× ×
−
− = 2,56.1016 m.s—1.
On notera que C doit être exprimée en mol.m—3 dans ce calcul.
Q30 : Lorsque les solutions sont très concentrées, le coefficient d’activité des espèces solubilisées
n’est plus voisin de 1. On ne peut plus remplacer les activités par les concentrations dans les rela-
tions thermodynamiques.
Q31 : L’oxyde cuivreux n’est pas stable à pH = 0 d’après le diagramme potentiel-pH. Il est oxydé
en Cu2+ et réduit en Cu(S) suivant le bilan:
Cu2O(S) + 2 (H3O+)aq = Cu(S) + (Cu2+)aq + 3 H2O.
Q32 : L’élément Cu de Cu2O est oxydé et réduit: il subit une dismutation.
Q33 : Le tétraaquocuivre(II) possède 4 molécules d’eau comme ligand.
Sa formule est donc [Cu(H2O)4]2+.
Q34 : La formule développée plane de ce complexe est la suivante:
Q35 : A l’anode se produit l’oxydation. La seule espèce susceptible
d’être oxydée dans la solution est H2O.
On a donc 3 H2O → ½ O2 + 2 H3O+ + 2 e—;
A la cathode se produit la réduction. Les espèces susceptibles d’être réduite sont Cu2+ et H2O.
Il se produit (Cu2+)aq + 2 e— → Cu(S) à cause de la valeur des potentiels standard.
Q36 : Le bilan global de la réaction mise en jeu dans l’électrolyseur est donc
(Cu2+)aq + 3 H2O = ½ O2 + 2 H3O+ + Cu(S)
Q37 : Par définition, l’affinité thermodynamique est
A= − ° −
F
H
G
G
I
K
J
J
+
+
∆G T RT p
c p
( ) ln H O O
Cu
3
2
2
1 2
2 0 0 1 2
b
g
ch
/
/
. . .
Le phénomène n’est pas spontané puisque c’est une électrolyse. Donc la condition d’évolution est
A.dξ < 0. Pour une évolution non spontanée dans le sens direct du bilan, il faut A < 0.
PARTIE V
Q38 : Le bilan (3) est une combinaison linéaire des bilans (1) et (2) selon (3) = 2×(1) – (2) donc
∆rG3°(T) = 2×∆rG1°(T) – ∆rG2°(T).
A.N. ∆rG3°(T) = –292000 + 220,8. T en J.mol–1.
Q39 : L’oxyde de cuivre (I) est Cu2O. Il se dismute en Cu et CuO suivant le bilan :
Cu2O(S) = Cu(S) + CuO(S)
ce qui correspond à la combinaison linéaire (1/4)[(3) – (2)].
Q40 : On applique la règle de Gibbs v = c + 2* – ϕ avec
Ÿ c = 3 – 1 = 2 constituants indépendants ;
Ÿ 2* = 1 car ∆rH° ≠ 0 donc T est facteur d’équilibre mais p n’est pas facteur d’équilibre car
il n’y a pas d’espèce gazeuse.
Ÿ ϕ = 3 car il y a trois espèces solides.
On obtient donc v = 0. On ne peut pas choisir la valeur de T pour réaliser cet équilibre. La condition
d’équilibre s’écrivant K° = 1 puisque les activités des solides sont égales à 1, l’équilibre existe à la
température telle que ∆rG°(TEQ) = -RT LnK° = 0 d’où ∆rG3°(TEQ) = ∆rG2°(TEQ). Cela nécessite
H2
O
OH2
H2O
H2O
Cu
2+