Parallélogrammes

Figures élémentaires de géométrie : trapèzes et parallélogrammes
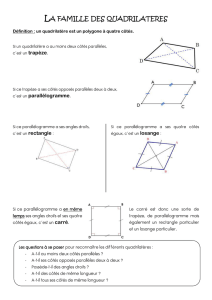
Définition : On appelle quadrilatère toute figure composée de 4 sommets et 4 côtés.
(Chaque sommet est le point de départ de deux segments).
1- Le trapèze
Définition : On dit qu’un quadrilatère est un trapèze lorsque 2 de ses côtés sont parallèles.
Définition : On appelle trapèze rectangle un trapèze ayant un angle droit.
Définition : On appelle trapèze régulier un trapèze dont les côtés obliques ont la même
longueur.
2- Le parallélogramme
Définition : On dit qu’un quadrilatère est un parallélogramme lorsque ses côtés opposés
sont parallèles 2 à 2.
1/2
Les quadrilatères
I

Propriété 1 : Un parallélogramme admet un centre de symétrie qui est le point d’intersection
de ses deux diagonales.
Conséquences : a) Les diagonales d’un parallélogramme se coupent en leur milieu.
b) Les angles opposés d’un parallélogramme ont la même mesure.
c) Les côtés opposés d’un parallélogramme ont la même longueur.
Remarque : un parallélogramme est un trapèze particulier.
Autrement dit : Tous les parallélogrammes font partie de la famille des trapèze.
Par contre, les trapèzes ne sont pas tous des parallélogrammes.
Propriété 2 : Un quadrilatère (convexe) ayant 2 côtés parallèles et de même longueur est un
parallélogramme.
Propriété 3 : Un quadrilatère (convexe) ayant les côtés opposés de même longueur est un
parallélogramme.
2/2
Les quadrilatères
I
I
I