UE4-Fonctions numériques

Fonctions numériques
A l'école élémentaire, à travers diverses activités proposées aux enfants, il est possible de rencontrer plusieurs
types de fonctions numériques. En voici quelques unes. Pour chacune d'entre elles, essayez de proposer d'autres
types de désignation que celle utilisée.
1) Voici un tableau donnant les prix de places de cinémas en fonction de leur nombre :
nombre de places
1
2
3
5
10
...
prix en euros
8
16
24
40
80
...
2) le prix d’une course en taxi est constitué d’une partie fixe ou prise en charge (3 euros) et d’une partie
proportionnelle à la distance parcourue(0,5 euros par kilomètre).
3) Un magasin de location de VTT propose les tarifs suivants:
- pour moins de trois heures, on paie un forfait de 25€ et 10€ de l'heure.
- De trois heures à moins de 15 heures, on paie un forfait de 25€ et 8€ de l’heure.
- De 15 heures à moins de 24 heures, on paie un forfait de 150€.
Toute heure commencée est due.
4)La distance nécessaire pour freiner sur route sèche en fonction de la vitesse est donnée dans le tableau
suivant:
vitesse en km/h
0
10
20
30
40
50
60
70
distance de freinage en
m
0
1
4
9
16
25
36
49
5) Un rectangle a pour aire 84 cm2 . Pour des valeurs données d'une dimension on peut trouver la valeur de
l'autre.
6) Il y a bien longtemps, le général romain Térence demanda à être récompensé pour les nombreuses victoires
qu'il avait remportées. L'empereur lui proposa de puiser des sesterces dans son trésor personnel de la manière
suivante :
Tu en prendras un le premier jour, 2 le deuxième jour, 4 le troisième jour et ainsi de suite en doublant
chaque jour le nombre de pièces emportées la veille.
7) Comment traduire la variation des restes des divisions euclidiennes d'un nombre entier naturel par 5 ?
8) Trouvez, en fonction de sa longueur, la largeur d'un rectangle de périmètre 84 cm.
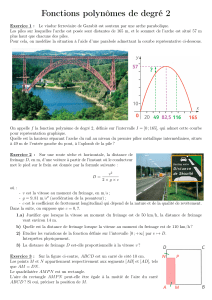
Exercice 1 : Amiens 2000-2
Voici deux propositions de tarifs de location de vélos.
location du camping :
Moins de 8 jours : 15€ par jour et par vélo
8 jours ou plus : forfait de 40€ plus 10€ par jour et par vélo
Location de la plage :
12,5€ par jour et par vélo
Clara souhaite louer un vélo au tarif le plus intéressant.
1) Où doit-elle s'adresser si elle souhaite louer son vélo pendant 12 jours ? 20 jours ?
2) Clara a loué au camping et Paul a loué à la plage.
Pour une même durée de location, ils ont payé la même somme.
Déterminez par le calcul la durée de location.
3) a) Sur un même graphique, représentez l’évolution du coût de la location en fonction de la durée pour les 2
types de contrat.
b) Retrouvez le résultat obtenu à la question 2.
c) Comparez les 2 types de contrat d’un point de vue financier.
Exercice 2 sujet 1-2011
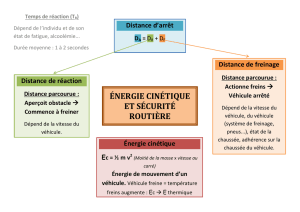
Le temps de réaction est le temps qui sépare le moment où le conducteur voit un obstacle de
celui où il commence à appuyer sur la pédale de frein. Dans tout le problème on considère que
le temps de réaction est d’une seconde.
On note DR la distance parcourue pendant le temps de réaction.
La distance de freinage DF d’un véhicule est la distance parcourue durant le freinage du
véhicule jusqu’à l’arrêt complet.
Le graphique ci-dessous indique la distance de freinage en fonction de la vitesse du véhicule
au moment du début du freinage.
La distance d’arrêt DA d’un véhicule est la distance parcourue par le véhicule entre le moment
où le conducteur voit un obstacle et commence à freiner et celui où le véhicule s’arrête.
On a l’égalité DA = DR + DF.
a) A l’aide du graphique, indiquer la distance de freinage, au mètre près, pour la vitesse
v1 = 90 km/h, puis pour la vitesse v2 = 130 km/h.
b) Calculer la distance d’arrêt, au mètre près, lorsque le véhicule roule à la vitesse v1, puis à la
vitesse v2.
c) A quelle vitesse en km/h roule l’automobiliste si la distance parcourue pendant le temps de
réaction est 15 mètres ?
d) Déterminer la distance d’arrêt à un mètre près.
Exercice 3 sujet 2-2011
On étudie la fonction f qui, à la vitesse v d’un véhicule (exprimée en mètre par seconde)
associe la distance de freinage (exprimée en mètre).
Cette fonction est définie par f : v → k x v2 , où k est un coefficient qui dépend notamment de
l’état de la route.
€
Partie 1
Dans des conditions « normales », lorsque la route est sèche, le coefficient k est égal à 0,08.
1. On utilise un tableur pour créer le tableau de valeurs ci-après :
a) Donner une formule qui, entrée dans la cellule B2 (puis recopiée vers la droite), permet de
compléter la ligne 2.
b) On veut qu’en modifiant la valeur de k en B3, les distances soient recalculées
automatiquement. La formule proposée au a) satisfait-elle cette nouvelle contrainte ?
Si oui, pourquoi ? Si non, en proposer une autre qui convient.
2. a) Calculer la distance de freinage sur route sèche pour une vitesse de 72 km/h.
b) À partir de quelle vitesse (arrondie à l’unité, en km/h), la distance de freinage sur route
sèche est-elle supérieure à 45 mètres ?
Partie 2 :
Sur une route mouillée, le coefficient k est différent de 0,08.
Après avoir modifié la valeur de k dans la feuille de calcul précédente, on a construit la
représentation graphique qui donne la distance de freinage sur route mouillée en fonction de
la vitesse.
1. En utilisant cette représentation graphique, estimer la valeur du coefficient k sur route
mouillée.
2. Où se situerait la représentation graphique donnant la distance de freinage sur route sèche
en fonction de la vitesse, par rapport à la représentation graphique tracée ? Justifier la réponse
par le calcul.
Exercice 4 groupe 5 2008
Un fabricant de parfum veut fabriquer deux flacons de même contenance, suivant les schémas ci-dessous.
L’unité de longueur est le centimètre.
1) Le flacon 1 est constitué de deux pavés droits.
x désigne la mesure de la hauteur du pavé droit supérieur.
Montrer que la mesure V1 du volume du flacon 1 s’exprime en fonction de x sous la forme :
V1(x) = 2 x + 100
2
x
1
5
Flacon 1
4
5
2) Le flacon 2 est constitué
− d’une pyramide tronquée à base rectangulaire identique au solide ABCDEFGH de la figure 1. La droite
(SO) est la hauteur de la pyramide ; elle perce le rectangle EFGH en O’. On donne: SO = 11 cm;
SO’ = 5,5 cm; AB = 6 cm; BC = 4 cm; EF = 3 cm; FG = 2 cm,
− et d’un pavé droit de dimensions 2, 3, et x comme indiqué ci-dessous.
S
2
H
E
x
G
O
’ F
3
C
D
4
O
A
B
figure 1
6
Flacon 2
Montrer que la mesure V2 du volume du flacon 2 s’exprime en fonction de x sous la forme :
V2(x) = 6 x + 77
On rappelle que le volume d’une pyramide est donné par la formule :
1
V = (aire de la base × hauteur de la pyramide).
3
3) Dans un repère orthogonal du plan :
− sur l’axe des abscisses, un centimètre représente une longueur de 1 cm,
− sur l’axe des ordonnées, un millimètre représente un volume de 1 cm3.
a) Représenter graphiquement, dans ce repère, les fonctions V1 et V2 pour des valeurs de x comprises entre 0
et 10.
b) Déterminer graphiquement une valeur approchée de x au dixième près pour laquelle V1(x) = V2(x).
c) Résoudre l’équation V1(x) = V2(x) par le calcul.
d) Calculer le volume correspondant à la valeur x trouvée précédemment et l’exprimer en centilitre.
Exercice 5 :(extrait sujet groupe6 2006)
Le jardin de monsieur Durand a la forme d’un trapèze rectangle, ABCD, tel que AB = 50 m, AD = 30 m,


DC = 70 m. Les angles A et D sont droits.
Soit M un point du segment [AB]. On pose AM = x.
La parallèle à la droite (AD) passant par M coupe la droite (DC) en G. Le jardin est ainsi partagé en deux
parties :
− le rectangle AMGD qui est le potager ;
− le reste qui est la pelouse.
1) Calculer l’aire du jardin.
2) Exprimer en fonction de x, l’aire du rectangle AMGD (le potager). En déduire l’aire de la pelouse BCGM.
3) Pour quelle valeur de x la pelouse et le potager ont-ils la même aire ? Quelle est alors la forme du potager.
Justifier les réponses.
4)
a. Représenter sur un même graphique, les fonctions donnant l’aire du potager AMGD et l’aire de la pelouse
BCGM en fonction de x. On utilisera pour cela la feuille de papier millimétré et on prendra comme unités
graphiques : 1 cm pour 10 mètres sur l’axe des abscisses, 1 cm pour 100 m2 sur l’axe des ordonnées.
La feuille de papier millimétré est à rendre avec la copie.
b. Retrouver graphiquement le résultat de la question 3. Expliquer.
5) Sachant que dix kilos de semences sont nécessaires pour une pelouse de 500 m2, quelle quantité est
nécessaire pour ensemencer 900 m2 ?
. Exercice 6
Monsieur Martin possède un capital de 10 000 euros qu'il veut faire fructifier. Il hésite entre deux sortes de
placement:
- le placement P rapporte 8% par an. Les intérêts sont versés chaque année et ne s'ajoutent pas au capital. Il
s'agit d'intérêts simples. Ils sont soumis à une imposition annuelle de 15%.
- le placement Q rapporte 5% par an net d'impôts. A la fin de chaque année, les intérêts sont ajoutés au capital.
Il s'agit d'intérêts composés. On appellera intérêts nets d'impôts les intérêts perçus après imposition.
1) Etude du placement P
a) Pour un capital placé de 10 000 euros, calculez les intérêts nets acquis au bout d'un an après l'imposition.
b) Par rapport au capital, calculez le pourcentage que représentent ces intérêts nets.
c) Soit S le total des 10 000 F placés et des intérêts nets acquis réellement au bout de n années.
Exprimez S en fonction de n.
Si l'on note S = f(n), n étant un nombre entier quelconque, quelle est la forme de la représentation graphique de
S?
2) Etude du placement Q :
Pour les deux questions a) et b) qui suivent, on suppose que le capital placé vaut C.
a) Avec le placement Q, exprimez, en fonction de C, le capital obtenu au bout d'un an.
b) Donnez l'expression, que l'on notera g (n), de la valeur acquise par le capital C au bout de n années. Aucune
démonstration n'est demandée.
3) Comparaison des deux placements
On se propose de faire une représentation graphique permettant de comparer les deux formules pour un capital
de
10 000 euros.
Pour cela, utilisez le document joint en annexe 1 sur lequel figure la représentation graphique de la fonction g
(n) définie à la question 2b)
a) Représentez graphiquement, sur ce document, la fonction f (n) définie à la question lc).
b) Pour un placement d'une durée de huit ans, déterminez graphiquement le placement que Monsieur Martin a
intérêt à choisir en expliquant votre réponse.
c) On appelle n0, le nombre entier non nul d'années de placement pour lequel les deux sortes de placements sont
équivalentes.
A l'aide d'une lecture graphique, déterminez n0 .
Par le calcul, déterminez l'écart entre les deux valeurs acquises par ce capital au terme de ces n0 années.
Annexe1 :
Exercice 7 AIX 2000-1
La figure F ci-dessous est constituée d'un demi-cercle de diamètre [BC] de centre O et de rayon 1, et des côtés
[AB], [CD], [DA] du carré ABCD.
1) Calculez l'aire A de la surface S délimitée par F.
2) La figure F est la trajectoire, d'origine A, du point mobile M qui se déplace dans le sens des aiguilles d'une
montre.
Le réel x désigne la distance parcourue par le point M depuis son départ de A.
On associe, à x, l'aire, notée A(x), de la surface balayée par le segment [OM] pendant le déplacement de M.
Démontrez l'égalité A(x) =
x
2
dans les trois cas suivants :
a) M appartient au segment [AB].
b) M appartient au demi-cercle d'extrémités B et C.
c) M appartient au segment [CD].
3) Le point mobile M s'arrête en un point P au moment où l'aire de la surface balayée par le segment [OM] est le
€ la surface S.
quart de l'aire de
a) Calculez la distance exacte x parcourue par le point M à ce moment-là.
b) Faites une figure et placez le point P de manière précise en justifiant sa position.