chimie -méca-sujetA.11PYPLME1

11PYPLME1
1
BACCALAUREAT TECHNOLOGIQUE
Session 2011
Épreuve :
PHYSIQUE – CHIMIE – ÉLECTRICITÉ
Partie :
MÉCANIQUE – FLUIDIQUE - CHIMIE
Série
SCIENCES ET TECHNOLOGIE DE LABORATOIRE
PHYSIQUE DE LABORATOIRE ET
DE PROCÉDÉS INDUSTRIELS
Durée de l'épreuve : 3 heures coefficient : 5
L'usage de la calculatrice est autorisé.
Le sujet comporte 9 pages.
LE CANDIDAT COMPOSERA LA PARTIE CHIMIE ET
LA PARTIE MÉCANIQUE SUR DEUX COPIES SÉPARÉES

11PYPLME1
2
Partie Chimie : Les propriétés du cuivre (8 points)
Le cuivre est l’un des rares métaux que l’on trouve à l’état pur dans la nature (mines
de cuivre).
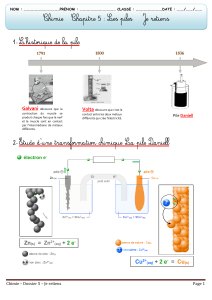
Ses propriétés permettent des utilisations variées : il a été utilisé dans la première
pile électrique de Volta, actuellement dans les câbles électriques et les
microprocesseurs.
Les scientifiques ont réussi à obtenir des isotopes du cuivre utilisés dans le secteur
de la médecine nucléaire (radiothérapie) grâce à leurs propriétés radioactives.
Cette étude des propriétés du cuivre comporte deux parties indépendantes :
• Fonctionnement d’une pile cuivre- nickel,
• Radioactivité d’un isotope artificiel du cuivre.
A . Etude d’une pile (4,5 points)
On se propose dans cette première partie d’étudier la propriété conductrice du
cuivre naturel, dans le fonctionnement d’une pile cuivre – nickel.
Données :
Masse molaire :
Chlorure de nickel II : M
NiCl2
= 129,6 g. mol
-1
Potentiels standards :
E°
Cu2+/Cu
= + 0,34 V
E°
Ni2+/Ni
= - 0,25 V
Relation de Nernst :
Pour une demi équation du type a ox + n e
-
= b red
ox désignant l’oxydant et red le réducteur, la loi de Nernst donne l’expression
du potentiel correspondant pour l’oxydant et le réducteur en solution :
E
ox / red
= E°
ox / red
+
n
0,06 log (
b
red
a
ox
C
C)
avec C
ox
et C
red
concentrations molaires de l’oxydant et du réducteur
Dans le cas particulier où le réducteur est à l’état métallique, la relation de
Nernst s’écrit :
E
ox / red
= E°
ox / red
+ n
0,06 log (
a
ox
C )

11PYPLME1
3
1- On prépare par dissolution :
- Une solution (S
1
) de chlorure de nickel II de volume V
1
= 250,0 mL et de
concentration C
1
= 0,216 mol. L
-1
,
- Une solution (S
2
) de sulfate de cuivre II de volume V
2
= 250,0 mL et de
concentration C
2
= 0,238 mol. L
-1
.
a) Ecrire l’équation de dissolution du chlorure de nickel II dans l’eau.
b) Calculer la masse m
1
de chlorure de nickel II solide à peser pour préparer la
solution (S
1
).
c) Décrire le mode opératoire permettant de réaliser la solution (S
1
) de chlorure de
nickel II en précisant la verrerie utilisée.
2- On réalise une pile « nickel-cuivre » en associant les deux demi-piles suivantes :
• Demi-pile N° 1 : Electrode de nickel plongeant dans la solution de chlorure de
nickel II (S
1
),
• Demi-pile N° 2 : Electrode de cuivre plongeant dans la solution de sulfate de
cuivre II (S
2
).
a) Ecrire, pour chaque couple redox, la demi-équation correspondante.
b) Calculer les potentiels E
1
et E
2
de chaque demi-pile.
c) En déduire la force électromotrice de la pile en début de fonctionnement.
d) Faire le schéma annoté de la pile débitant dans un récepteur, en indiquant les
polarités des électrodes, le sens de circulation des électrons et celui du courant.
e) Déduire du schéma et de la question 2.a) l’équation de la réaction globale lorsque
la pile délivre du courant.
B . Radioactivité du cuivre (3,5 points)
Dans cette partie on se propose d’étudier les propriétés radioactives d’un des
isotopes artificiels du cuivre.
Données :
Extrait de la classification périodique :
Elément Co Ni Cu Zn Ga Ge
Numéro
atomique (Z)
27 28 29 30 31 32
Loi de décroissance radioactive : ln ( 0
A
A) =
- λ t ou A = A
0
e
- λ t
A représente l’activité de l’échantillon à l’instant t
A
0
représente l’activité de l’échantillon à l’instant t = 0
λ est la constante de désintégration radioactive

11PYPLME1
4
1- Le cuivre naturel possède principalement deux isotopes
63
Cu et
65
Cu.
a) Définir le terme « isotopes ».
b) Donner la composition du noyau
63
Cu.
2- Pour le traitement des cancers, on utilise l’isotope artificiel du cuivre
67
Cu,
émetteur β
-
, dont la période radioactive est suffisamment courte, ce qui permet aux
patients de sortir rapidement après traitement.
a) Préciser la nature de la particule émise lors d’une désintégration de type β
-
.
b) S’agit-il d’une réaction nucléaire spontanée ou provoquée ?
c) Ecrire l’équation de la réaction de désintégration du nucléide
67
Cu en précisant
les lois utilisées.
La période radioactive de l’isotope
67
Cu est T = 62 h.
d) Définir en une phrase la période radioactive.
e) Montrer que λ = T2 ln .
f) Calculer la valeur de la constante radioactive λ de
67
Cu en précisant l’unité.
g) Du cuivre
67
Cu ayant été administré au patient, ce dernier est autorisé à sortir
lorsque l’activité de l’isotope devient égale à 80 % de son activité initiale.
Au bout de combien de temps le patient peut-il quitter l’hôpital ?
h) Selon vous, quels sont les moyens de protection utilisés autour d’une enceinte
de radiothérapie ?

11PYPLME1
5
Partie Mécanique/Fluidique (12 points)
A – Principe de l’expérience de CAVENDISH (6 points)
Henry Cavendish (1731 – 1810)
« J’ai pesé la Terre ! » aurait déclaré Cavendish en 1798. En effet, grâce à la mise au
point d’une astucieuse balance de torsion (photo ci-dessous), il venait de mesurer
les infimes forces de pesanteur qui agissent entre des masses ordinaires. Ceci lui
permettait de déterminer la valeur de la constante universelle de gravitation G
intervenant dans la loi de Newton énoncée en 1687.
L’expérience de Cavendish a permis d’établir une valeur de référence pour la
constante universelle de gravitation que nous noterons G
référence
.
Cette valeur (6,67 x 10
-11
N.m².kg
-2
) a permis le calcul de la masse de la Terre :
M = 6 x 10
24
kg.