DS en Seconde

CLASSE : 2nde CONTROLE sur le chapitre :
Géométrie dans l'espace
Durée approximative : 2 h
La calculatrice est autorisée.
EXERCICE 1 / 4 points Difficulté :
On considère un triangle ABC rectangle en A tel que AB = 5 cm et AC = 3 cm.
1. Donner le nom du solide (S) engendré par la rotation du triangle ABC autour de la droite (AB).
2. Calculer le volume de (S) en cm3.
3. Dessiner un patron de (S).
EXERCICE 2 / 3 points Difficulté :
On place dans un cube de côté 10 dm une boule tangente à ses 6 faces.
1. Calculer le rapport du volume de la boule sur celui du cube..
2. Calculer ensuite le rapport de la surface de la boule sur celle du cube.
3. Que penser de ces rapports pour des cubes d'autres dimensions ?
EXERCICE 3 / 3 points Difficulté :
On considère l'algorithme suivant :
Nom : MonAlgo
Entrées : deux réels notés X et Y
Sortie : le volume V d'un certain solide
Variables : deux réels V1 et V2
Début
V1 prend la valeur de pi*X^2*Y
V2 prend la valeur de 1/3*pi*X^2*Y
V prend la valeur de V1+V2
Renvoyer « le volume est : » V
Fin
1. Que renvoie cet algorithme pour X=2 et Y=3 ?
2. V1 et V2 sont en fait les volumes de deux solides usuels. Quels sont ces deux solides ?
Préciser leurs éléments caractéristiques pour qu'ils correspondent aux calculs de l'algorithme.
3. Représenter en perspective un solide dont le volume V serait donné par cet algorithme.
EXERCICE 4 / 3 points Difficulté :
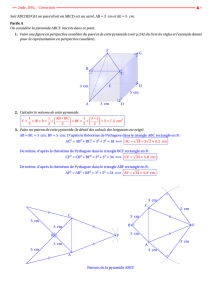
Soit SABCD la pyramide de sommet S représentée sur la feuille annexe.
Les constructions suivantes sont à faire sur la feuille :
1. Construire le point I, intersection de (BC) et (AD).
2. Déterminer et construire, en rouge, l'intersection des plans (SBC) et (SAD).
3. Déterminer et construire, en bleu, l'intersection des plans (SBD) et (SAC).
Ce devoir n'est qu'un exemple. En aucun cas il ne constitue un modèle.

EXERCICE 5 / 7 points Difficulté :
Soit SABCD une pyramide régulière à base carrée et de sommet S dont les arêtes ont toute une
mesure égale à 10 m. On note O le centre de ABCD.
Partie A (3 points)
1. Calculer AO.
2. En déduire que
SO =5 2
m.
3. Calculer la valeur exacte du volume de cette pyramide puis une valeur approchée au litre
près.
Partie B (4 points)
Soit A' un point sur l'arête [SA]. Le plan passant par A' et parallèle au plan (ABC) coupe [SB] en B' ,
[SC] en C' et [SD] en D'. On pose SA' = x et on note V la fonction qui à x associe le volume V(x) de la
pyramide régulière SA'B'C'D' à base carrée et de sommet S.
1. Pierre, élève de Seconde pense que le tableau de variations de la fonction V est celui-ci :
x0 + ∞
Variations de V
10
0
a. Ce tableau comporte des erreurs. En citer deux en justifiant les raisons pour lesquelles
Pierre s'est trompé.
b. Donner un tableau de variations plus cohérent.
2. Jacques, élève de Seconde aussi, a utilisé un logiciel pour obtenir la courbe représentative de
V sur [3;6] :
Il en déduit que lorsque x = 5, le volume de SA'B'C'D' n'est pas égal à la moitié de celui de
SABCD. Qu'en pensez-vous ?
3. Exprimer V(x) en fonction de x.
Ce devoir n'est qu'un exemple. En aucun cas il ne constitue un modèle.

CLASSE : 2nde ANNEXE
Géométrie : Espace
Figure de l'exercice 4.
Ce devoir n'est qu'un exemple. En aucun cas il ne constitue un modèle.