DS 4 le second degré Exercice 1: discriminant (8pts) 1. Résoudre

DS 4 le second degré
Exercice 1: discriminant (8pts)
1. Résoudre 4x2+17x−15 =0.
2. Résoudre 4x2+17x−15 ≤0.
3. (a) Donner la forme factorisée de 4x2+17x−15.
(b) Résoudre 4x2+17x−15 +(x+5)(x2−2x)=0.
(c) Simplifier 4x2+17x−15
4x−3.
Exercice 2: œufs (5pts)
Trois concurrents lancent des œufs au dessus de leur tête respective. Marc a son œuf qui a pour altitude z0(t)=
−5t2+10t+2, celui de Piotr z1(t)=−5t2+14t+2 et enfin celui de Naranbaatar z2(t)=−5t2+8t+2. Les altitudes sont
données en mètres.
1. Ils ont lâché l’œuf au niveau de leur tête et le chronomètre s’est enclenché (t=0s). Quelle est la taille des inter-
venants ?
2. Quel est l’œuf qui est allé le plus haut ? Préciser les altitudes maximales des œufs.
3. Combien de temps l’œuf de Naranbataar est resté en l’air avant de s’écraser violemment sur sa tête ?
Exercice 3: liens entre coefficients et courbes (4pts)
On sait que très peu de choses sur chacun des polynômes du second degré P,Q,R,S, les nombres a,b,c,x2sont
différents et inconnus pour chacun d’eux. Les quatre polynômes sont différents.
P(x)=a(x−5)(x+x2)
Q(x)=−2x2+bx +cet a un discriminant
positif.
R(x)=ax2+bx +cavec −b
2a=2.
S(x) a un discriminant négatif.
2
4
6
8
10
12
14
16
−2
−4
123456−1−2−3
C1
C2C3C4
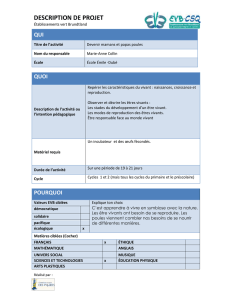
1. Dire quelles sont les représentations graphiques de chacun d’eux (C1est la courbe de P,Q,Rou S?).
2. Justifier ses choix.
Exercice 4: œufs la suite (3pts)
Naranbataar vient de recevoir son œuf sur la tête.
Gengis Khan, fou de rage devant un tel spectacle, décide de lancer l’œuf à plus de 20 mètres au dessus de sa tête.
1. Quelles sont les valeurs de bqui conviennent (si z3(t)= −5t2+bt +2) ?
2. Calculer en fonction de ble temps nécessaire pour voir Gengis Khan convulser car il aura reçu son œuf sur la
tête.
3. Donner un programme qui demande la valeur de bpuis calcule et affiche le temps avant réception de l’œuf.

DS 4 correction le second degré
Exercice 1: discriminant (8pts)
1. Résoudre 4x2+17x−15 =0.
C’est une équation du second degré avec a=4,b=17,c=-15. On calcule donc le discriminant ∆=172−4×4×(−15) =529. Comme ∆>0il y a
deux solutions. x1=−17 −p529
8=−5et x2=3 4.
2. Résoudre 4x2+17x−15 ≤0.
On forme le tableau de signes en pensant « qu’à l’intérieur »des racines le signe est celui de −a= −4. Ainsi les solutions sont dans l’intervalle
·−5; 3
4¸.
3. (a) Donner la forme factorisée de 4x2+17x−15.
∆est positif donc la forme factorisée est du type a(x−x1)(x−x2)soit ici 4(x−(−5))µx−3
4¶=4(x+5)µx−3 4¶
(b) Résoudre 4x2+17x−15 +(x+5)(x2−2x)=0. Développer conduit à un polynôme du troisième degré. Il existe des formules. Mais
nous ne les connaissons pas. On tente donc de remplacer le polynôme par sa forme factorisée. 4x2+17x−15 +(x+5)(x2−2x)=0
⇔4(x+5)³x−3
4´+(x+5)(x2−2x)=0
⇔(x+5)h4³x−3
4´+(x2−2x)i=0⇔(x+5)£4x−3+x2−2x¤=0
⇔(x+5)£x2+2x−3¤=0⇔x+5=0ou x2+2x−3=0On reconnait une autre équation du second degré qui a pour discriminant
∆=16 donc deux solutions que l’on sait calculer.
⇔x=−5ou x =1ou x =−3
(c) Simplifier 4x2+17x−15
4x−3.
4x2+17x−15
4x−3=
4(x+5)³x−3
4´
4x−3=(x+5)(4x−3) 4x−3=x+5pour x 6= 3
4.
Exercice 2: œufs (5pts)
Trois concurrents lancent des œufs au dessus de leur tête respective. Marc a son œuf qui a pour altitude z0(t)= −5t2+10t+2, celui de Piotr
z1(t)=−5t2+14t+2 et enfin celui de Naranbaatar z2(t)= −5t2+8t+2. Les altitudes sont données en mètres.
1. Ils ont lâché l’œuf au niveau de leur tête et le chronomètre s’est enclenché (t=0s). Quelle est la taille des intervenants ?En remplaçant t par
0on trouve 2m pour tous.
2. Quel est l’œuf qui est allé le plus haut ? Préciser les altitudes maximales des œufs.L’extremum est atteint en t =−b
2a. Vu que a = −5pour les
trois polynômes on aura bien un maximum en cette valeur. Pour z0le plus haut point est atteint en t =1s et vaut 7m. Pour z1le plus haut
point est atteint en t =1,4s et vaut 11,8m. Pour z2le plus haut point est atteint en t =0,8s et vaut 5,2m. Piotr a lancé son œuf plus haut.
3. Combien de temps l’œuf de Naranbataar est resté en l’air avant de s’écraser violemment sur sa tête ? On cherche quand l’œuf est à une
altitude de 2m. Soit z2(t)=2⇔ −5t2+8t=0⇔t=0s ou t =1,6s. On n’est pas trop surpris de voir que l’oeuf met autant de temps pour
redescendre qu’il avait mis pour monter 0,8s +0,8s.
Exercice 3: liens entre coefficients et courbes (4pts )
On sait que très peu de choses sur chacun des polynômes du second degré P,Q,R,S, les nombres a,b,c,x2sont différents et inconnus pour
chacun d’eux. Les quatre polynômes sont différents.
P(x)=a(x−5)(x+x2)
Q(x)=−2x2+bx +cet a un discriminant positif.
R(x)=ax2+bx +cavec −b
2a=2.
S(x) a un discriminant négatif.
2
4
6
8
10
12
14
16
−2
−4
1 2 3 4 5 6−1−2−3
C1
C2C3C4
P admet une racine 5donc sa courbe passe par (5,0) et C4est la seule à passer par ce point.
Q a sa courbe tournée vers le bas et traverse l’axe des abscisses deux fois mais plusieurs courbes sont dans ce cas.
R a son extremum en x =2donc forcément sa courbe est C3et celle de Q est forcément C2
S a sa courbe qui ne rencontre pas l’axe des abscisses donc elle est C1
Exercice 4: œufs la suite (3pts)
Naranbataar vient de recevoir son œuf sur la tête.
Gengis Khan, fou de rage devant un tel spectacle, décide de lancer l’œuf à plus de 20 mètres au dessus de sa tête.
1. Quelles sont les valeurs de bqui conviennent (si z3(t)= −5t2+bt +2) ? Il faut que z3(t)=20 ait au moins une solution dans [0;+∞[. Le
discriminant de −5t2+bt −18 doit être positif ou nul. ∆=b2−360 ≥0est équivalent à b ∈]−∞;−6p10]∪[6p10;+∞[. Mais le maximum est
atteint en −b
2aon devine que si b est négatif la solution serait dans les temps négatifs. Le tableau de variation en apporte la preuve. Il faut donc
b>0soit b ∈[6p10;+∞[.
2. Calculer en fonction de ble temps nécessaire pour voir Gengis Khan convulser car il aura reçu son œuf sur la tête. item Il faut résoudre
z3(t)=2 donc −5t2+bt =0 ou encore t=0sou t=b
5. Gengis Khan doit attendre b/5 secondes.
3. Donner un programme qui demande la valeur de bpuis calcule et affiche le temps avant réception de l’œuf.
0 b=input ( ’ valeur de b ? ’ )
i f b<=0:
print ( ’aucune chance de
recev oi r son oeuf sur
la tet e ’ )
i f b>0:
print ( b/5 , ’ secondes avant
reception ’ )

DM 7 second degré
1. Le polynôme P(x)=x2+4x+ca son coefficient cobtenu par un lancer de dé. Le dé a six faces.
(a) Calculer les racines de Psuivant les valeurs de c.
(b) Quelle est la probabilité que le polynôme n’ait pas de racine ?
2. Développer a(x−x1)(x−x2) et déterminer la valeur de a,bet cen fonction de celles de a,x1et x2.
3. Sur python recopier, puis faire tourner le programme (on pourra répondre faux pour voir ce qu’il se passe).
0import random
reponse_correcte= False
nombre_tentatives=0
while not ( repon se_corr ecte ) :
x1=random . randi nt ( 1 ,1 1)
5 x2=random . randi nt ( 1 ,1 1)
a=1
b=x1+x2
c=x1*x2
print ( ’ quel les sont l e s s ol uti on s de x^2+ ’ , b, ’ x+ ’ , c , ’ =0? ’ )
10 xx1=input ( ’ x1 ? ’ )
xx2=input ( ’ x2 ? ’ )
i f ( ( x1== f l o a t ( xx1 ) ) and (( x2== f l oa t ( xx2 ) ) ) or ( x2== fl o at ( xx1 ) ) and ( x1== f l o a t ( xx2 ) ) ) :
reponse_correcte=True
el se :
15 print ( ’non l es bonnes reponses et a i e n t x1= ’ , x1 , ’ e t x2= ’ , x2 )
nombre_tentatives=nombre_tentatives+1
print ( ’ ex er ci ce r e u s s i en ’ , nombre_tentatives , ’ t entative ( s ) ’ )
4. Modifier le programme pour qu’il demande 10 équations et affiche la note obtenu sur 20.
5. Modifier le programme pour que les équations aient un coefficient anon nul mais différent de 1 (attention les coefficients bet cchangent.
DM 7 second degré
1. Le polynôme P(x)=x2+4x+ca son coefficient cobtenu par un lancer de dé. Le dé a six faces.
(a) Calculer les racines de Psuivant les valeurs de c.
(b) Quelle est la probabilité que le polynôme n’ait pas de racine ?
2. Développer a(x−x1)(x−x2) et déterminer la valeur de a,bet cen fonction de celles de a,x1et x2.
3. Sur python recopier, puis faire tourner le programme (on pourra répondre faux pour voir ce qu’il se passe).
0import random
reponse_correcte= False
nombre_tentatives=0
while not ( repon se_corr ecte ) :
x1=random . randi nt ( 1 ,1 1)
5 x2=random . randi nt ( 1 ,1 1)
a=1
b=x1+x2
c=x1*x2
print ( ’ quel les sont l e s s ol uti on s de x^2+ ’ , b, ’ x+ ’ , c , ’ =0? ’ )
10 xx1=input ( ’ x1 ? ’ )
xx2=input ( ’ x2 ? ’ )
i f ( ( x1== f l o a t ( xx1 ) ) and (( x2== f l oa t ( xx2 ) ) ) or ( x2== fl o at ( xx1 ) ) and ( x1== f l o a t ( xx2 ) ) ) :
reponse_correcte=True
el se :
15 print ( ’non l es bonnes reponses et a i e n t x1= ’ , x1 , ’ e t x2= ’ , x2 )
nombre_tentatives=nombre_tentatives+1
print ( ’ ex er ci ce r e u s s i en ’ , nombre_tentatives , ’ t entative ( s ) ’ )
4. Modifier le programme pour qu’il demande 10 équations et affiche la note obtenu sur 20.
5. Modifier le programme pour que les équations aient un coefficient anon nul mais différent de 1 (attention les coefficients bet cchangent.