PST- Solides 2

Muriel Fénichel – Mai 2011
L3- PST-Pre-CRPE
Culture mathématique – Géométrie
Activités autour des solides
Cours du 17/05/2010
1. Dualité
On considère un cube ABCDEFGH.
On appelle I, J, K, L, M et N les centres des faces
ABCD, EFGH, BHCG, ABHE, DAEF et CDFG.
On joint I à K, I à M, l à L, et I à N..
On joint J à K, J à M, J à L et J à N.
On obtient ainsi un polyèdre.
Décrire ce polyèdre (nombre de faces, de sommets et
d’arêtes et nature des faces)
Le polyèdre obtenu possède :
• 6 sommets qui sont les centres des faces du
cube : I, J, K, l, M et N.
• 2 arêtes [IK], [IL], [IM], [IN], [JL], [JK], [JM],
[JN], [KM], [ML], [LN] et [KN]
• 8 faces.
Montrons que ces faces sont des triangles équilatéraux
isométriques.
Traçons les diagonales [BD], [BE] et [DE] des faces
carrées ABCD, ABHE et AEFD du cube.
Si a est la mesure de la longueur de l’arête du cube, la
mesure de la longueur de ces diagonales est a 2
I est le milieu de [BD] et M est le milieu de [DE]. Dans
le triangle BDE, I et M sont donc les milieux de deux
côtés. D’après le théorème de la droite des milieux, IM est égal à la moitié de DE soit a 2 /2.
On démontrerait de la même manière que [IL], et [LM] ont pour mesure de longueur a 2 /2.
Le triangle IML est donc équilatéral.
On pourrait faire la même démonstration pour toutes les faces du polyèdre.
Ce polyèdre est donc un octaèdre régulier.
2. Polyèdres tronqués
Activité 1 : tétraèdre tronqué
On considère un tétraèdre régulier en bois dont la mesure de longueur de chaque arête est a.
On tronque ce tétraèdre en coupant le morceau obtenu à partir de chaque sommet en retirant le tiers de chaque
arête.
Indiquer le nombre de faces, de sommets et d’arêtes du nouveau solide en précisant la nature des faces.
Le solide obtenu est un tétraèdre tronqué. A chaque sommet du tétraèdre, on a enlevé un
petit tétraèdre dont la mesure de la longueur de l’arête est a/3.
Les sections obtenues à chaque sommet sont des triangles équilatéraux. Il y en a quatre.
Les faces du tétraèdre initial sont remplacées par des hexagones réguliers. Il y en a quatre.
Le solide obtenu a donc 8 faces dont 4 sont des hexagones réguliers et 4 sont des triangles
équilatéraux.
Il a 12 sommets.
Il a 18 arêtes.
De chaque sommet partent 2 hexagones et un triangle équilatéral.
Ce n’est pas un polyèdre régulier puisque ses faces ne sont pas des polygones identiques.
A
B
C
D
F E
H
G
I
M
L
J
K
N
A
B C D
E
F
I
K
G
L
J H

Muriel Fénichel – Mai 2011
Activité 2 : cube tronqué
On considère un cube en bois dont la mesure de longueur de chaque arête est b.
On tronque ce cube en coupant le morceau obtenu à partir de chaque sommet en retirant la moitié de chaque
arête.
Décrire le nouveau solide obtenu.
Le solide obtenu est un cube tronqué. A chaque sommet du cube, on a enlevé un tétraèdre non régulier puisque
ses faces ne sont pas des triangles équilatéraux identiques. Trois de ces faces sont des triangles isocèles dont les
côtés égaux ont pour mesure de longueur b/2 et dont le troisième côté est la diagonale d’un carré dont la mesure
de longueur du côté est b/2, soit b 2 /2 ( application du théorème de Pythagore (cf chapitre 1 partie géométrie).
Les sections obtenues à chaque sommet du cube sont des triangles équilatéraux dont le côté a pour mesure de
longueur b 2 /2.
Les faces du cube sont remplacées par des carrés dont les sommets sont les milieux des arêtes du cube et dont la
mesure de longueur du côté est b 2 /2.
Le solide obtenu a 14 faces : 8 sont des triangles équilatéraux, 6 sont des carrés. Il a 12 sommets et 24 arêtes.
De chaque sommet partent 2 triangles équilatéraux et 2 carrés.
Ce n’est pas un polyèdre régulier puisque ses faces ne sont pas des polygones identiques.
Ce solide s’appelle un cuboctaèdre
3. Représentations planes des solides
Plusieurs représentations d’un solide sur un plan peuvent être envisagées : une perspective centrale, une
perspective parallèle (cavalière ou axonométrique), une représentation des différentes vues, un patron.
Ce passage de l’espace à la représentation plane entraîne la perte de certaines informations. C’est ce qui explique
l’existence de plusieurs types de représentations planes, chacune conservant et transmettant certaines
informations au détriment d’autres.
1
Une représentation ne peut rendre compte à la fois de la vision d’un objet et de ce que l’on sait de lui. On retrouve
le conflit entre le « voir » et le « savoir ». Il faut alors prendre en compte ce qu’on attend d’une représentation.
Perspective cavalière
La perspective cavalière résulte d’une projection oblique sur un plan appelé plan de projection. La projection se fait
dans une même direction.
Exemple 1 : Cube projeté sur un plan parallèle à la face de devant.
Pour comprendre la projection permettant de donner cette représentation à partir
d’un cube posé sur un plan horizontal, on peut imaginer des segments obliques et
parallèles partant de chaque sommet du cube et arrivant sur un plan vertical. La
figure, formée sur ce plan, en reliant les points intersections des segments et du
plan vertical, est une perspective cavalière du cube.
Cette figure ne contient véritablement que deux carrés. Pourtant, elle représente
un cube constitué de six carrés. Les faces parallèles au plan de projection ne sont
pas déformées. De façon générale, les éléments situés dans des plans parallèles
au plan de projection sont conservés. Les arêtes du cube qui sont
perpendiculaires au plan de projection sont représentées par des droites parallèles appelées fuyantes. L’angle
formé par ces fuyantes et la direction horizontale caractérise la perspective cavalière choisie, le plus souvent
l’angle est égal à 45°, mais parfois il peut aussi valoir 30°. Les dimensions des segments portés par les fuyantes
sont, en général, réduites par rapport aux dimensions réelles. Le rapport de réduction est aussi une caractéristique
de la perspective cavalière.
Le parallélisme des droites est conservé ainsi que le rapport des longueurs de segments parallèles.
Pour des éléments qui ne sont pas situés dans des plans parallèles au plan de projection, les distances, les angles
ne sont pas conservés ce qui peut être traduit par la non conservation des formes géométrique des faces.
L’alignement des points est conservé : des points alignés dans l’espace le sont sur la représentation mais la
réciproque est fausse en général. Des droites qui paraissent se couper sur la représentation peuvent ne pas être
concourantes dans la réalité.
Remarque : cette perspective aurait été utilisée par les militaires pour dessiner des projets de fortification et de
terrassement, c’est la raison pour laquelle on lui donne aussi le nom de perspective militaire. L’avantage de cette
1
D’après l’ouvrage Rouche N., Lismont L. (2001) , Formes et mouvements. Perspectives pour l’enseignement de la géométrie, Centre de
recherche de l’enseignement des mathématiques

Muriel Fénichel – Mai 2011
représentation est qu’elle permet d’effectuer des mesures sur le dessin quand on en connaît les caractéristiques :
l’angle que font les fuyantes avec la direction horizontale et le rapport de réduction mentionné précédemment.
Perspective centrale
Exemple du cube :
Les angles, le parallélisme, l’orthogonalité, les longueurs, les rapports de longueur ne sont en général pas
conservés dans ce type de représentation. Par contre, la forme et les rapports de longueur d’un objet situé dans un
plan parallèle au plan de projection sont conservés.
Remarque : on peut envisager aussi des perspectives centrales avec plusieurs points de fuite mais à l’école
élémentaire seule la perspective centrale à un point de fuite est abordée par l’utilisation de photos. Ces dernières
ont l’avantage de fixer le plus fidèlement possible la perception visuelle et ainsi d’en permettre la conservation.
Projections orthogonales (Vues)
Une vue d’un solide est une représentation plane qui provient d’une projection orthogonale sur un plan parallèle à
une face.
Exemple : Vue de dessus d’un cube.
Pour comprendre la projection permettant d’obtenir cette vue de dessus à partir d’un
cube posé sur un plan horizontal, on peut imaginer des segments verticaux partant des
sommets du solide et arrivant sur un plan horizontal.
Suivant le plan sur lequel le solide est projeté, différentes vues sont possibles : vue de
dessus (le plan est parallèle à la face de dessus), vue de droite (le plan est parallèle à
la face de droite), vue de face…
Le dessin technique utilise ce type de représentation. Pour qu’un objet puisse être construit à partir des différentes
vues, trois vues sont nécessaires : vue de face, de droite, de dessus ainsi que des conventions de traçage. En
particulier, ce qui est vu est formé avec des traits pleins, ce qui est caché avec des traits en pointillé
On peut aussi évoquer le mot « empreinte ».
Pour un prisme droit posé sur sa base, la vue de dessus correspond à l’empreinte du prisme. La vue de dessus du
cube donné en exemple précédemment correspond à l’empreinte du cube. Par contre, pour un solide quelconque,
l’empreinte est souvent différente de la vue de dessus. L’empreinte d’une boule est un point alors que sa vue de
dessus est un disque. On pourrait dire que la vue de dessus est le « trou » que ferait un solide dans un plan si on
l’enfonçait perpendiculairement à ce plan. On a ainsi une bonne illustration d’un exemple d’une projection
orthogonale d’un solide pour des élèves de l’école élémentaire
Patron
Un patron d’un solide est une surface plane qui permet de reconstruire le solide uniquement par pliage et sans
recouvrement ; ou, en reprenant la définition de Gobert (2001), « un patron de solide est un dessin, où toutes les
faces du solide sont représentées, toutes juxtaposées les unes aux autres, permettant après découpage du
contour et pliage suivant les segments, de reconstituer le solide en volume »
2
Le terme de développement du solide s’emploie quelquefois à la place du mot patron.
Gobert (ibid.) effectue deux types de remarques : celles concernant le patron à partir du solide et celles concernant
le solide à partir du patron.
A partir du patron :
« Deux faces adjacentes sur le patron sont toujours adjacentes sur le solide. Mais attention, deux faces qui ne sont
pas l’une à côté de l’autre sur le patron peuvent être des faces adjacentes sur le solide, ou ne pas être des faces
adjacentes sur le solide. »
« Un segment commun à deux faces sur le patron est une arête du solide. Mais on peut avoir deux segments sur
le patron qui correspondent à une même arête du solide »
2
GOBERT S.(2001) Questions de didactique liées au rapport entre la géométrie et l’espace sensible, dans le cadre de l’enseignement à l’école
primaire, thèse Université Paris VII: p. 143
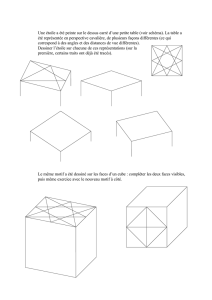
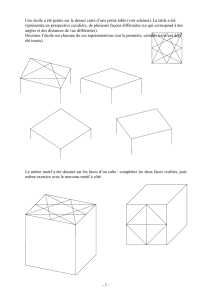
Pour représenter un cube, on peut utiliser une perspective centrale
à un point de fuite
: on choisit une ligne d’horizon, un point de fuite
sur cette ligne et on projette sur un plan vertical appelé plan du
tableau. Toute arête vertica
le du cube est représentée par un
segment vertical dans le plan du tableau, toute arête horizontale du
cube parallèle au plan du tableau est représentée par une droite
horizontale dans le plan du tableau. Toutes les autres arêtes se
rejoignent au point de fuite.

Muriel Fénichel – Mai 2011
A partir du solide :
« Deux faces adjacentes sur le solide peuvent être adjacentes sur le patron ou ne pas l’être. Par contre, deux
faces non adjacentes sur le solide ne peuvent jamais être adjacentes sur le patron »
« Une arête d’un solide peut être représentée une ou deux fois sur un patron du solide »
« Un sommet du solide peut être représenté par un ou plusieurs points sur le patron »
3
« Ces connaissances sont en jeu dans les activités proposées en général aux élèves. Elles sont très rarement
formulées, et pourtant elles permettent d’avoir des repères qui peuvent faciliter, améliorer, faire progresser la
capacité à remonter un patron en volume dans sa tête et à lire sur les patrons les propriétés du solide »
4
Un polyèdre peut avoir plusieurs patrons différents. Exemple : Le cube a onze patrons.
Certains solides ne sont pas développables ; ils n’ont pas de patron. Exemple : La boule.
4. Eléments de corrigé des exercices (cours du 17/05/2011)
4.1 Les patrons de la pyramide
Voici les 6 patrons non donnés dans l'énoncé (il fallait en dessiner 3 à main levée).
4.2 Le patron du tétraèdre tronqué
Nommons les sommets dans l’ordre alphabétique en ne différenciant les occurrences d’un même sommet que par
un changement d’indice :
Nous avons utilisé les lettres de A à L, il y a donc 12 sommets. La
formule de Descartes-Euler nous permet de calculer le nombre
d’arêtes : 18 (8 + 12 − 2)
Remarque : On aurait pu dénombrer directement les arêtes,
contrairement aux sommets dont le nombre d'occurrences peut varier
(une pour A, B, C, D, E et F, deux pour J et K, trois pour G, H, I et L) il
y a une ou deux occurrences pour les arêtes. Une pour celles
communes à deux faces sur le patron (elles sont au nombre de 7 : 6
pour l'hexagone central et 1 commune à l'hexagone et le triangle en
bas à droite sur le patron) et deux pour les autres qui sont au nombre
de 22 et qui comptent donc pour 11. Cela fait 18 arêtes en tout.
3
GOBERT S.(2001) : p. 143
4
GOBERT S.(2001) : p. 143
B A
F
C
D E
G
1
G
2
G
3
G
1
H
1
H
2
H
3
I
1
I
2
I
3
J
1
J
2
K
1
K
2
L
1
L
2
L
3

Muriel Fénichel – Mai 2011
Ci-dessous sont coloriés de la même couleur les côtés des polygones qui vont se juxtaposer pour former une
arête lorsqu’on pliera le patron
4.3 Les 11 patrons du cube
A
A
2
B
1
B
2
C
D
E
F
G
H
I
1
I
2
I
3
B
3
A
3
J
1
K
1
L
1
L
2
L
3
J
2
K
2