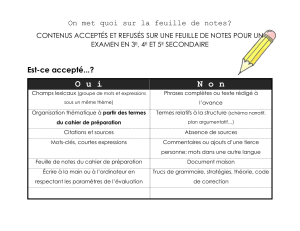
Feuille d`exercices

EXERCICES ET PROBLÈMES
Ch. 7 : Calcul littéral - Développement
: Oral : Application : Approfondissement
Rappels
1Calculer chacune des expressions suivantes
pour a= 2 et b= 1
1. 3a
2. 5−4a
3. −5x2+ 9
4. 2ab
5. −5(a+b)
6. 3b2−2a
2Calculer chacune des expressions suivant pour
a=1
2et b=2 3.
1. 4a−6b
2. 5a−9b
3. 7(a+b)
4. 2ab
3
1. Développer les expressions données.
(a) 7y(−2x−5)
(b) b(−2b−4,3)
(c) (4 + 2y)(−3,5)
(d) 53
10 +2 5x
2. Factoriser les expressions données.
(a) 5a−5b
(b) 6x−18a
(c) 42 + 28y
(d) −5a2+ 10
4L’aire d’un triangle est 14x+ 7x2où xdé-
signe un nombre positif. La longueur d’une de ses
hauteurs est égale à 7x.
1. (a) Factoriser l’expression 14x+ 7x2
(b) En déduire la longueur du côté relatif à
la hauteur indiquée.
2. On donne x= 1,5cm, dessiner un tel tri-
angle en vraie grandeur et calculer son aire.
Réduction
5Réduire chaque expression dès que c’est pos-
sible !
1. 2x+ 5x
2. 8y−5x
3. 9b−4b
4. 3x+ 2y+ 2z+t
5. −4a+ 8b−9b+ 4a
6. −10x+ 7y+ 5y+ 20x
6Réduire les expressions données.
1. 3x2+ 5x2−x2
2. 7x+ 5 + 9a−6 + x−6a
3. 3x2+ 5x−10x2
4. 10x−15 + x2−12x
5. 45x2−10x+ 35x2+ 8x−3+2x
6. −7y−5y2+ 10y+ 3y2−3y
7Monsieur Ledoux souhaite faire peindre le
mot BOULANGERIE sur la façade de son nouveau
magasin. Il estime que toutes les lettres de ce mot
sauf la lettre I doivent avoir une largeur de xcm,
que la lettre Idoit avoir pour largeur x
3cm et que
l’espace entre deux lettres doit être de x
2cm.
1. Exprimer en fonction de xla longueur to-
tale du mot BOULANGERIE à peindre, et
réduire l’expression.
2. La façade du magasin de Monsieur Ledoux
mesure 3,22 m de long. Quelle sera en cm
la largueur maximale de cahcune des lettres
peintes ?
8Le cercle C1a pour centre Iet diamètre x.
Le cercle C2a pour centre Jet diamètre 2x, où x
désigne un nombre positif.

1. Montrer que la longueur du cercle Cde dia-
mètre 3xest égale à la somme des longueur
des cercles C1et C2.
2. Montrer que l’aire de la partie colorée en
bleu est égale à celle d’un disque de rayon
x.
Supprimer parenthèses
9Supprimer les parenthèses de chaque expres-
sion puis la réduire.
1. 5 + (3x+ 2)
2. 2y+ (6 −3y)
3. 3b+ (−5b−7)
4. 4−(3y+ 1)
5. 2x−(−3x−6)
6. 5a−(−3a+ 4)
10 Pour chacune des expressions suivantes, sup-
primer les parenthèses puis réduire.
1. 4x−(3x+ 5)
2. 21 −(x−3−5y)
3. −5−(−1 + x−2y) + (3x−2y)
4. 7x2−(9x−5) + (1 −x2+x)
11 
1. Développer les produits : −2(3y−6y2+ 4)
et 3(−2−4y).
2. En déduire la forme réduite de l’expression
B=−2(3y−6y2+ 4) + 3(−2−4y).
12 Aïcha achète 5cahiers, 3stylos et 2pa-
quets de copies. Un cahier coûte 0,30 ede plus
qu’un stylo et le prix d’un paquet de copie est le
double de celuid’un cahier.
On note xle prix, en euros, d’un stylo.
1. Exprimer en fonction de x
(a) le prix d’un cahier ;
(b) le prix d’un paquet de copies ;
(c) le montant total des achats d’Aïcha. On
donnera le résultat sous sa forme déve-
loppée et réduite.
2. Un stylo coûté 1e. Quel est le montant des
achats d’Aïcha.
Double distributivité
13 Dans chaque égalité, dire quel terme le
complète.
1. (2x−3)(x+ 7) = 2x2+. . . −3x−21
2. (x−6)(9 + x)=9x+. . . −. . . −6x
3. (1 −5x)(2x+ 1) = 2x+ 1 −. . . −. . .
4. (4x+ 1)(1 −5x) = . . . −20x2+ 1 −. . .
14 Développer et réduire les expressions don-
nées.
1. (1 + 3x)(7 + 5x)
2. (10x+ 9)(10 + 9x)
3. (−6 + x)(3 −x)
4. (8a−5)(−a+ 2)
5. 3
2−x(4x−6)
6. 3x+2
5(−2 + 2x 3)
15 
1. Calculer le produit (7x−5)(2 −3x)pour
x= 10 sans le développer.
2. Développer et réduire le produit (7x−5)(2−
3x).
3. Remplacer xpar 10 dans l’expression obte-
nue à la question précédente et vérifier que
le résultat est identique à celui obtenu à la
première question.
16 On considère le programme de calcul :
— Choisir un nombre de départ.
— Multiplier ce nombre par −2.

— Ajouter 5au produit.
— Multiplier le résultat par 5.
— Écrire le résultat obtenu.
1. Vérifier que lorsque le nombre de départ est
2, on obtient 5.
2. Arthur prétend que, pour n’importe quel
nombre de départ x, l’expression (x−5)(x−
5) −x2permet d’obtenir le résultat du pro-
gramme de calcul. A-t-il raison ?
Problèmes
17 Réduire le plus possible, l’expression
R=n+ 1
n−n n−1.
18 Attention à la canicule !
En France, on mesure la température en degrés
Celsius (◦C) alors qu’en Grande-Bretagne, on la me-
sure en degrés Fahrenheit (◦F).
Voici une formule permettant de convertir des
◦C en ◦F :
TF=9×TC
5+ 32,
où TFest la température en ◦F et TCla température
en ◦C.
1. Quelle température en ◦F correspond à une
température de 20◦C
2. Kévin affirme que le record de chaleur en Eu-
rope est de 100◦F ; Gaïa lui rétorque que lors
d’une canicule les températures ont dépassé
ce record et ont atteint 42◦C. Qui a tort ?
19 Distance de sécurité
La distance de sécurité entre deux véhicules en
mouvement est la distance minimale qu’il faut lais-
ser entre les deux pour éviter une collision si le pre-
mier véhicule freine. Pour calculer la distance de sé-
curité entre deux véhicules, on admet qu’un conduc-
teur met deux secondes à réagir en cas de freinage
d’urgence. Elle se calcule de la façon suivante :
dS =V×1000
3600 ×2,
dS est la distance de sécuité en m et Vest la vitesse
de déplacement en km/h.
On rappelle que toute vitesse se calcule à l’aide
de la formule V=d
t, où Vreprésente la vitesse en
km/h, dla distance parcourue en km et tle temps
en heures.
1. Expliquer la formule de calcul de la distance
de sécurité dS.
2. Calculer, en mètres, la distance de sécurité
à laisser entre deux véhicules roulant à 90
km/h.
3. Sylvie affirme que, pour calculer la distance
de sécurité, il faut utiliser la formule sui-
vante : dS =V×0,56. A-t-elle raison ? Ex-
pliquer la réponse.
20 Ne t’emballe pas !
Le débit cardiaque est souvent mesuré chez les
personnes cardiaques ou les sportifs.
On l’obtient par la formule suivante : DC=
F×V, avec :
—DC: débit cardiaque (L/min),
—F: fréquence cardiaque (batte-
ments/minute),
—V: volume de sang ejecté par le coeur par
battement (L/battement).
1. Quel est le débit cardiaque d’un homme
dont la fréquence cardiaque est de 70 batte-
ments/minute et dont le coeur éjecte 7cL
de sang par battement ?
2. Expliquer pourquoi F=DC
V.
3. La tachycardie est une maladie qui concerne
les personnes ayant une fréquence cardiaque
supérieure à100 battements/minute.
Un homme au repos dont le débit cardiaque
est égal à 5L/min et dont le volume de sang
éjecté par le coeur est de 0,045L/battement
est-il atteint de tachycardie ?
4. Le débit cardiaque augmente lorsqu’une per-
sonne a une activité physique, ou est sou-
mise à un stress ou une émotion forte. De
façon quotidienne, au cours de la digestion
des repas, le débit cardiaque augmente car
l’appareil digestif a besoin de sang supplé-
mentaire.
On dit que le débit augmente de 10% envi-
ron pour la digestion d’un petit déjeuner et
qu’il augmente de 30% lors de la digestion
d’un repas normal.

Calculer le débit cardiaque durant ces deux
types de digestion chez une femme dont
la fréquence cardiaque au repos est de 75
battements/min et dont le volume de sang
éjecté par le coeur est de 4,8cL/battement.