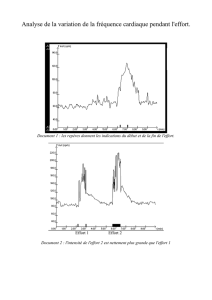
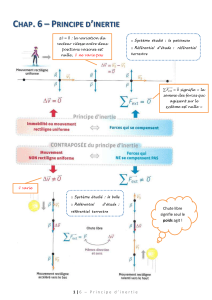
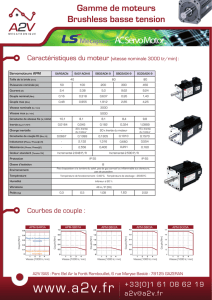
TALK CH3-web

Ch. III GEOMETRIE DES MASSES
I. Masse
1. Définition
• strictement positive : m (S) > 0
• additive : (extensive)
• invariante : même valeur dans tous les référentiels
• conservée pour un système fermé (solide par exemple) :
dm
dt
= 0
2. Système discret : (S)= ensemble de N points matériels de masse mi () :
3. Système continu :(S) = solide
dm :masse élémentaire d’un élément de matière de (S)
Distribution Volumique de masse volumique ρ
ρ ρ
ρ:
: :
:
ρ
ρρ
ρ = Cte : 
Distribution Surfacique de masse surfacique σ
σ σ
σ:
::
:
σ
σσ
σ = Cte. m = σ s

Distribution Linéique de masse linéique λ
λλ
λ :
II. Centre d’inertie
1. Définition
Système discret
Le ce
ntre d’inertie (ou centre de masse) d’un système matériel (S), constitué d’un ensemble de N points
matériels Mi, de masse mi (), est le point géométrique G tel que :
i
Il s’agit du barycentre des points matériels Mi pondérés par leur masse mi.
Si A est un point quelconque de l’espace, alors :
i
Système Continu
Si A est un point quelconque de l’espace:

2. Méthodes de détermination du centre d’inertie
2.1 Calcul direct
(O; ,, ) : repère orthonormé direct.
G : Centre d’inertie d’un système matériel (S) : 
Système discret
(S) = { N points matériels Mi () }, respectivement, de masse mi.
Vecteur position, dans (): 
Coordonnées de G:
Système continu
M : point matériel quelconque de (S)
Vecteur position dans (): 
Coordonnées de G :

Exemple : Demi-disque homogène de rayon R
Le demi-disque est dans le plan (xOy) :
z = 0 donc z
G
= 0
Coordonnées polaires  
Surface élémentaire : 
Masse élémentaire : 
Système homogène : σ
σσ
σ = Cte donc  et 
Coordonnées du centre d’inertie, G :
Donc le centre de masse G a pour coordonnées dans ():
G
O
θ
θθ
θ
r
dr
y
x

2.2 Utilisation de la symétrie
Le centre d’inertie, G d’un système (S) est un point invariant
des opérations de symétrie et par conséquent, il appartient
aux éléments de symétrie de (S).
Symétrie par rotation : G appartient à l’axe de rotation
Symétrie plane (miroir) : G appartient au plan de symétrie.
Exemple : Demi-disque homogène de rayon R
Le plan (yOz) est un plan de symétrie (miroir).
Donc le centre d’inertie G appartient au plan (yOz).
Par conséquent : x
G
= 0
G
y
x