Chapitre 8 bis: Énergie mécanique

Chapitre 8 bis:
Énergie mécanique
A) Le travail est-ce de l’énergie fournie?
1) Qu’est-ce que l’énergie potentielle mécanique? C’est la capacité que possède un
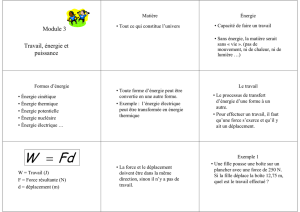
corps à faire un travail mécanique. Le travail mécanique c’est l’énergie qu’il faut
déployer pour déplacer un objet en exerçant une certaine force (W = F x ∆s).
Symbole: Ep Unité: le joule (J)
2) a) Quelle est l’énergie qu’il faut fournir si on veut soulever un objet? L’énergie
nécessaire pour appliquer une force qui vaincra le poids de l’objet et l’amènera à
la hauteur désiré.
b) Qu’est-ce que l’énergie potentielle gravitationnelle? c’est l’énergie emmagasinée
par un corps lorsqu’il est soulevé à une certaine hauteur.
formule algébrique: Ep = m x g x h
Ep: énergie potentielle en joules (J)
m: masse du corps en kilogrammes (kg)
g: accélération gravitationnelle en mètre par seconde au carré (m/s2)
h: hauteur du corps en mètres (m)
c) Quel est votre énergie potentielle gravitationnelle en ce moment? Elle dépend
de la hauteur de référence. Elle diffèrera selon que je la calcule à partir du
plancher de la classe, du derrière ou du devant de l’école.
Exercice: Quelle est l’énergie potentielle gravitationnelle d’un litre d’eau situé à
70,0 m de hauteur? Ep = 686 J
masse volumique de H2O = 1,00 g/mL
V = 1,00 L mH2O = 1 000 mL x 1,00g/mL = 1 000 g = 1,00 kg
h = 70,0 m Ep = m x g x h
E
p = 1,00 kg x 9,80 m/s2 x 70,0 m
Ep = 686 J

B) Quand ça bouge, y a-t-il de l’énergie?
1) Qu’est que l’énergie cinétique? C’est l’énergie que possède un corps en
mouvement, de tout corps ayant une vitesse.
Symbole: Ek Unité: le joule (J)
2) De quoi dépend l’énergie cinétique? 1˚) de la masse du corps;
2˚) de la vitesse du corps.
formule algébrique: Ek = 1/2 x m x v2
EK: énergie cinétique en joules (J)
m: masse du corps en kilogrammes (kg)
v: vitesse du corps en mètre par seconde (m/s)
Exercice: Quelle est la quantité d’énergie cinétique d’un mètre cube d’air de 1,29
kg qui se déplace à une vitesse de 50,0 km/h? Ek = 124 J
m = 1,29 kg v = 50 000 m/3 600 s = 13,88888889 m/s
v = 50,0 km/h Ek = 1/2 x m x v2
Ek = 1/2 x 1,29 kg x (13,88888889 m/s)2 = 124,4212963 J
C) L’énergie se transforme-t-elle?
Pour un système donné, comment sont reliées l’énergie potentielle et l’énergie
cinétique? Quand on perd de l’un, on gagne de l’autre. L’énergie totale reste la
même: Esystème = Et = Ep + Ek
Exemple 1: Tarzan, dont la masse est de 90,0 kg, est debout sur une branche à
3,00 m du sol. Il prend sa liane et se laisse aller dans le vide.
Quelle sera sa vitesse lorsqu’il rasera le sol? v = 7,67 m/s
m = 90,0 kg Et=Ep1+Ek1 ------> Et = 90,0 kg x 9,80 m/s2 x 3,00 m + 0 J = 2 646 J
h = 3,00 m Et = Ep2 + Ek2 ------> 2 646 J = 0 J + 1/2 x 90,0 kg x v2
√ (2 646 J x 2/90,0 kg) = v
v = 7,668115805 m/s
Exemple 2: Un chariot de 500 g se déplace sur une table avec une vitesse de
10,0 m/s. Au bout de la table, il y a un plan incliné sans frottement.
Quelle hauteur atteindra-t-il sur ce plan incliné? h = 5,10 m
m = 0,500 kg Et = Ep1 + Ek1 ------> Et = 0 J + 1/2 x 0,500 kg x (10,0 m/s)2 = 25,0J
v = 10,0 m/s Et = Ep2 + Ek2 ------> 25,0 J = 0,500 kg x 9,80 m/s2 x h + 0 J
25,0 J/(0,500 kg x 9,80 m/s2) = h
h = 5,102040816 m

Exercices d’application
1) Zachary, dont la masse est de 55,0 kg, monte sur une chaise. Ses pieds se
retrouvent à 50,0 cm du sol.
a) Quelle quantité de travail a fait Zachary pour monter sur la chaise? Wf = 270 J
h = 50,0 cm = 0,500 m Fg = m x g = 55,0 kg x 9,80 m/s2 = 539 N
F = 200 N W = Fg x h = 539 N x 0,500 m = 269,5 J
b) Quelle serait sa vitesse en touchant le sol lorsqu’il se laisse tomber?
v = 3,13 m/s
m = 55,0 kg Et = Ep + Ek = 294 J + 0 J = 269,5 J (sur la chaise)
W = 200 N 269,5 J = 0 J + Ek ------> Ek = 269,5 J (au sol)
∆s = 50,0 cm Ek = m x v2/2 ------> 269,5 J = 55,0 kg x v2/2
Ff = 200 N v = √ (269,5 J x 2/55,0 kg) = 3,130495168 m/s
2) Un chat de 4,00 kg saute sur une branche située à 3,00 m de hauteur.
Quelle était sa vitesse de départ? v = 7,67 m/s
mchat = 4,00 kg Et = Ep + Ek = m x g x h + 0 J
h = 3,00 m Et = Ep = 4,00 kg x 9,80 m/s2 x 3,00 m = 117,6 J
g = 9,80 m/s2 Et = Ep + Ek = 0 J + m x v2/2 ------> 117,6 J = 4,00 kg x v2/2
v = √ (117,6 J x 2/4,00 kg) = 7,668115805 m/s
3) Une goutte d’eau de 0,0500 g quitte un nuage à 300 m d’altitude.
Quelle sera sa vitesse lorsqu’elle atteindra le sol? v = 76,7 m/s
m = 0,0500 g Ep = m x g x h = 0,0500 g x 1 kg/1 000 g x 9,80 m/s2 x 300 m
h = 300 m Et = Ep + Ek = 0,147 J + 0 J = 0,147 J
g = 9,80 m/s2 Et = Ep + Ek = 0 J + m x v2/2
0,147 J = 0,000 0500 kg x v2/2
v = √ (0,147 J x 2/0,000 0500 kg) = 76,68115805 m/s
4) Louis-Félix, avec son équipement de “snow”, a une masse de 65,0 kg. Il va à
une station de ski alpin où le sommet de la montagne est à 700 m.
Quelle quantité de travail mécanique doit faire le remonte-pente pour amener
Louis-Félix au sommet de la montagne? Wremonte-pente = 445 900J = 446 kJ
m = 65,0 kg Wremonte-pente = Ep = m x g x h
h = 700 m Wremonte-pente = 65,0 kg x 9,80 m/s2 x 700 m
g = 9,80 m/s2 Wremonte-pente = 445 900 J

5) Un train de montagnes russes pèse 1 500 kg. Le train est au repos à 40,0 m
du sol. On le laisse aller et il descend à 3,00 m du sol puis remonte et redescend
à 12,0 m du sol. (On néglige les forces de frottements.)
a) Quelle est l’énergie totale du train au point de départ? Et = 588 000 J
m = 1 500 kg Et = Ep + Ek = m x g x h + 0 J
hdépart = 40,0 m Et = 1 500 kg x 9,80 m/s2 x 40,0 m
Et = 588 000 J
b) Quelle est l’énergie cinétique du train au point le plus bas? Ek = 543 900 J
m = 1 500 kg Et = Ep + Ek = m x g x h + Ek
hbas = 3,00 m 588 000 J = 1 500 kg x 9,80 m/s2 x 3,00 m + Ek
Ek = 588 000 J - 44 100 J
E
k = 543 900 J
c) Quelle est la vitesse du train à 12,0 m du sol? v3 = 23,4 m/s
m = 1 500 kg Et = Ep + Ek = m x g x h3 + m x v32/2
h3 = 12,0 m 588 000 J = 1 500 kg x 9,80 m/s2 x 12,0 m + 1 500 kg x v32/2
v3 = √ ((588 000 J - 176 400 J) x 2/1 500 kg)
v
3 = 23,42648074 m/s
6) Simon lance un ballon de basketball, dont la masse est de 600 g, d’une
hauteur de 1,90 m jusqu’à une hauteur de 3,40 m.
Le panier est situé à 3,10 m.
a) Quelle quantité de travail a-t-il fournie pour lancer le ballon? WSimon = 8,82 J
m = 0,600 kg WSimon = Ep max - Ep départ = m x g x hmax - m x g x hdépart
hdépart = 1,40 m WSimon = 0,600 kg x 9,80 m/s2 (3,40 m - 1,90 m)
hmax = 3,40 m WSimon = 8,82 J
b) Quelle vitesse aura le ballon en entrant dans le panier? vballonl = 2,42 m/s
m = 0,600 kg Ek ballon = Ep max - Ep paniert = m x g x hmax - m x g x hpanier
hmax = 3,40 m Ek ballon = 0,600 kg x 9,80 m/s2 x (3,40 m - 3,10 m) = 1,764 J
hpanier = 3,10 m Ek ballon = m x vballon2/2
1,764 J = 0,600 kg x vballon2 /2
v = √ (1,764 x 2/0,600 kg) = 2,424871131 m/s