bac blanc 2015 / correcti̇on

BAC BLANC 2015 / CORRECTİON
1.1. Formule semi-développée de la molécule d'acide benzylique : (0,25 + 0,5 + 0,5)
C
CH
CH
CH
CH
CH
CC
COHO
CH
CH
CH
CH
CH
OH
1.2.1. Le carbone fonctionnel des groupements cétone est un site accepteur de doublets électroniques
du fait de la polarisation de la liaison C=O liée à la différence d’électronégativité χ(C) < χ(O)
L’oxygène de l’ion hydroxyde est donneur de doublets électroniques puisqu’il porte une charge
entière négative (et donc un doublet non liant). (0,5 + 0,5)
1.2.2. (0,25)
1.2.3. Le réactif A est l’ion hydronium H3O+.(0,25)
1.4. La phéromone proposée possède un atome de carbone asymétrique : d'où l'existence de deux
énantiomères.
Cette phéromone possède également une double liaison carbone carbone; ces carbones doublement liés
portent des substituants différents: d'où l'existence de deux diastéréoisomères (isomérie de type Z / E).
(1)
1.5.Pour qu'une molécule ait un effet biologique, elle doit interagir avec un site récepteur particulier de
l'organisme. Cette interaction se fait par l'intermédiaire d'un atome de carbone asymétrique : un seul des
deux énantiomères est donc efficace. (0,5)
1.6.Les pesticides, les insecticides se dégradent difficilement ; ils peuvent s'accumuler dans la chaîne
élémentaire et contaminer les milieux naturels. Ils ne sont donc plus adaptés. Par contre les phéromones
agissent à grande distance et à dose très faible. Elles n'ont pas les inconvénients des pesticides. Elles
sont donc mieux adaptées.(0,5)
2.1.La chlorose est due à un manque de chlorophylle. Ce manque peut être dû à un manque de fer. Un
produit anti-chlorose est donc riche en élément fer.(0,5)
EXERCİCE 1 : La chimie au service de la protection des plantes (9pts)
Groupe carboxyle ; fonction acide carboxylique
Groupe hydroxyle ; fonction hydroxyle
δ+
δ-
Θ

2.2.1.Dans le cas où une solution absorbe dans un seul domaine de longueur d’onde, sa couleur perçue
est la couleur complémentaire de celle des radiations absorbées.
Ainsi, la solution S1est de couleur pourpre car elle absorbe principalement dans le bleu (entre 500 et
520 nm).(0.5)
En travaillant à 510 nm, c.a.d au maximum d’absorbance de la solution on favorise la détection de l’infime
variation de la coloration.(0.25)
2.2.2.Lorsque la loi de Beer-Lambert est vérifiée, l’absorbance de la solution est proportionnelle à la
concentration de l’espèce colorée : A = k.c.
En traçant la courbe A=f(concentration), on obtient une droite passant par l’origine, ce qui correspond
bien à une situation de proportionnalité. (0.5Explications + 0.5 pour la courbe)
2.3.1. À partir de ce titrage, le jardinier désire déterminer le nom du produit commercial mis à sa
disposition.
Pour cela, tracer la droite moyenne passant au plus près de tous les points expérimentaux. On lit
l’abscisse du point d’ordonnée A = 0,302. On obtient une concentration en ions Fe2+d’environ
[Fe2+]’ = 3,6 mmol.L-1 (précision limitée due à une lecture graphique). Mais il s’agit là de la solution
diluée. D’après le protocole du document 6, une dilution par 100 a été réalisée donc
[Fe2+] = 3,6 .10-1mol.L-1
CmFe2+ = C * M = 3,6.10-1 * 56 = 2,0.101g.L-1
D’après le tableau du document 5, le produit anti-chlorose utilisé est le fer soni H39F.(1)
2.4.1.En utilisant les fonctions statistiques de la calculatrice :
moyenne :  = 3,64.10-3g.L-1 (0.25) et écart-type expérimental : σn–1 = 1,0656.10-4 (0.25).
L’incertitude élargie sur la moyenne est :
1
( ) . n U m k n
avec k =2 pour un intervalle de confiance de 95%
AN :U( ) = 2 *1,0656.10-4 /  = 7.10-5g.L-1(0.25) (on ne garde qu’un seul chiffre significatif sur
l’incertitude).
2.4.2.Cm = U( )
Cm = (3,64 0,07).10-3 ou 3,57mg.L-1< m <3,71mg.L-1avec un niveau de confiance de 95%. (0.25)

1. Détermination du caractère négatif de la charge de l’électron par J.J.Thomson
1.1. 
 dansle repère orthonormal et d’après l’échelle de 1,0 cm pour 5,0 kV.m-1, et
comme E = 15,0 kV.m-1, on en déduit que
E
sera représenté par une flèche de 3,0 cm.(0,25 )
Annexe exo2
1.2. Le document 3 indique que des particules de charges opposées s’attirent. Le faisceau d’électrons
étant attiré par la plaque chargée positivement, c’est que les électrons sont porteurs d’une charge
négative.(0,25 )
1.3.  (0,25 )
1.4. 
 soit 
 et enfin on a
(0,25 ). Ce qui fera 2,4 cm sur l’annexe exo 2, suivant (Oy) (0,25 )
1.5. Le poids 
du proton donc est sur (Oy) comme 
mais opposé à  .
Calculons l’intensité de P : P = mg = 9,11.10-31 9,80 = 8,9310-30 N. (0,25 )
Ainsi le rapport entre les intensités du poids et la force électrique est :
14
30
15
e102,69
108,93
102,40
P
F
La force électrique est environ 300 mille milliards de fois plus intense que le poids. Ce dernier
peut donc être largement négligé lors de l’étude du mouvement de l’électron entre les plaques.
(0,25 )
1.6. Entre les plaques, l’électron n’est soumis qu’à la force électrostatique (voir 1.5) qui le dévie vers la
plaque chargée positivement. Cette force est donc de sens opposé au champ électrostatique, et
comme , cela impose que q < 0. (0,25 )
2. Quelle condition sur E, pour que l'électron puisse ressortir sans toucher la plaque ?
2.1. On applique la deuxième loi de Newton au système électron, dans le référentiel terrestre supposé
galiléen.
dt
pd
Fext 
soit
amFext 
car la masse de l’électron est constante donc :
amFe
(0,25 )
soit
y
x
a
a
m
eE
0
d’où 
(0,25 )
Canon à
électrons
0
v
x
O
L
y
+ + + + + + + + + + + + +
–––––––––––––
E
A
H
EXERCİCE 2 : La deuxième expérience de J.J Thomson (6 points)

Le vecteur accélération est de sens opposé au vecteur champ
E
.
2.2. En intégrant l’accélération afin de trouver les équations horaires de la vitesse, on trouve :
 avec 
 d’où 
 (0,25 )
De la même façon, on intègre la vitesse afin de trouver les équations horaires de position et on
trouve :
² avec 
 d’où 
² soit 
(0,25 )
2.3. L’équation de la trajectoire est : d’après (1) on a : t = 
 soit en remplaçant dans (2) :
soit 
(0,25 )
2.4. Soit A le point de sortie du proton. Pour que l’électron ressorte des plaques sans en toucher une, il
faut que lorsqu’il atteint l’abscisse xA = L, son ordonnée yA soit inférieur à d. Donc, en utilisant
l’équation de la trajectoire, cela donne :
dyA
(0,25 ) soit
dx
mv
eE A 2
2
0
2
donc
dL
mv
eE  2
2
0
2
d’où
2
2
0
2eL dmv
E
(0,25 )
3. Comment varie la vitesse de l’électron entre les deux plaques ?
3.1. 
(0,25 )
3.2.  .
(0,25 ) donc 
 soit  (0,25 )
3.3. Ce travail étant positif, il est donc moteur. (0,25 )
3.4. é (0,25) or é 
 et 
 donc
(0,25 )
3.5. On a 
 donc  (0,25 ) soit 
 donc
soit (0,25 )
3.6. Il y a deux méthodes : soit on calcule numériquement vA et on compare vA et v0 soit on le fait sans
calcul numérique.
Méthode 1 : A.N : 
 soit 2,48.107 m.s-1
donc 
Méthode 2 (plus rapide) : 
 donc 
 or  sont positives donc
 soit (0,25 )

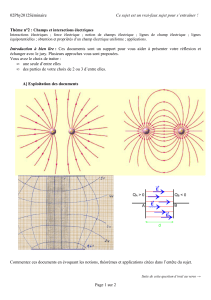
1) Dans l'océan la vitesse du son dépend de la profondeur.
D'après les documents 1 et 2, la profondeur optimale pour qu'une onde se propage dans un SOFAR
est situé à l'endroit pour lequel la variation de la vitesse du son s'annule.
Sur le doc 2, on mesure graphiquement une profondeur de 1100m (2 )
2) D'après le doc 3, le son émis par une baleine doit être atténué de 170-50=120 dB pour être au seuil
d'audibilité de la baleine. (1 )
Toujours d'après le doc3, la baleine émet des sons à une fréquence de 4000Hz
D'après le doc 4, à 4000 Hz, l'absorption par l'eau de mer est égale à 0,2 dB.km-1 (1 )
Pour trouver la distance maximale entre deux baleines pour qu'elles puissent communiquer, on fait
un calcul de proportionnalité :
120 dB ↔ dmax 0,2 dB ↔ 1 km
dmax = 120 / 0,2 = 600 km (1 )
Le résultat correspond à l'indication du texte d'introduction : " Ces messages peuvent, pour les grandes
espèces, être perçus à plusieurs centaines de kilomètres."
EXERCİCE 3 : La communication des baleines (5 s)