correction

FA1 correction
Partie 1!: Les caractéristiques de la croûte continentale
L’an dernier vous avez travaillé sur le domaine océanique.
Cette année, nous allons nous intéresser à la croûte continentale.
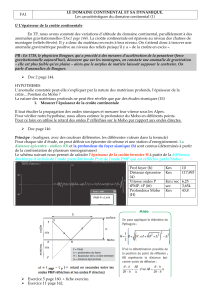
Le domaine continental se distingue du domaine
océanique par la nature de la croûte constitutive
de la lithosphère; ainsi
- Des zones immergées peuvent appartenir
au domaine continental (plateau
continental)
- Tandis que des zones émergées peuvent
être océaniques (Islande, la Réunion)
Croûte océanique
Croûte continentale
Schéma du profil A/B
A B
MANTEAU
?
A
B

I/ L’épaisseur de la croûte continentale
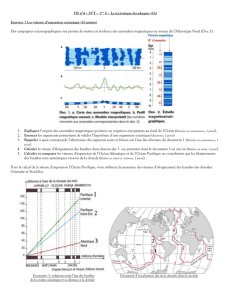
PB!: En 1738, le physicien Bouguer, qui a procédé à des mesures d’accélération de la pesanteur (force
gravitationnelle aujourd’hui), découvre que sur les montagnes, on constate une anomalie de gravitation
– elle est plus faible qu’en plaine – alors que le surplus de matière laissait supposer le contraire. On
parle d’anomalies de Bouguer.
 Doc 2 page 144. et ci-dessous!: anomalies gravimétrique au niveau des Alpes.
En TP, nous avons constaté des variations d’altitude du domaine
continental, parallèlement à des anomalies gravitationnelles (Doc1
page 144). La croûte continentale est épaissie au niveau des chaînes de
montagne (reliefs élevés). Il y a donc du matériau en excès à leur
niveau. On s’attend donc à trouver une anomalie gravimétrique
positive au niveau des reliefs puisqu’il y a « de la croûte en excès ».
HYPOTHESES
L’anomalie constatée peut-elle s’expliquer par la nature des matériaux
profonds, l’épaisseur de la croûte…Position du Moho ?
La nature des matériaux profonds ne peut être révélée que par des
études sismiques (1S)
Grâce à Google-earth, nous avons pu construire le profil de
profondeur du Moho. Il fait apparaître une «!racine!» crustale sous les
reliefs élevés.
Mais comment MESURER cette épaisseur!?
1. Mesurer l’épaisseur de la croûte continentale
Rappel sur la propagation des ondes P!: http://www.biologieenflash.net/animation.php?ref=geo-0031-1
Il faut étudier la propagation des ondes sismiques et mesurer leur vitesse sous les Alpes.
Pour vérifier notre hypothèse, nous allons estimer la profondeur du Moho en différents points.

Pour ce faire on utilise le retard des ondes P réfléchies sur le Moho par rapport aux ondes directes.
 Doc page 146
Comprendre le principe!:
La profondeur du Moho peut être calculée grâce aux enregistrements des séismes, en connaissant :
• La profondeur du foyer du séisme (= profondeur focale)
• La distance épicentrale (= distance de l'épicentre à la station d'enregistrement)
• La vitesse des ondes P (= 6,25 Km / s)
• Le retard des ondes PMP par rapport aux ondes P (calculé en secondes)
Il suffit de choisir une station sismique sur la carte des Alpes, par exemple, et d’appliquer la formule
tirée de la démonstration suivante!:
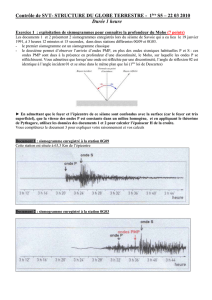
Données : les points remarquables!:
C : épicentre du séisme
D : station où le séisme est enregistré
F : Foyer du séisme
B : Point de réflexion des ondes P
!
Données : les distances!:
FD : trajet des ondes P directes
CD : distance de l'épicentre à la station
H : profondeur du Moho
h : profondeur du foyer du séisme
Données : les temps!: (lues sur le sismogramme)
t1 : temps d'arrivée des ondes directes P à la station D
t2 : temps d'arrivée des ondes PMP à la station D
δt = t2-t1
Au point D parviennent d'abord les ondes P directes selon le trajet FD puis un second train d'ondes P (=
ondes PMP) selon le trajet FB et BD; on nomme! dt! le retard des ondes PMP par rapport aux ondes P
Calcul de la profondeur du Moho
On connaît la vitesse des ondes P dans la croûte continentale dans les Alpes (V = 6,25 Km . s-1).
Si on considère le triangle rectangle FCD, le théorème de
Pythagore! permet d'écrire : FD2=FC2+CD2! .
En remplaçant par leurs valeurs, on obtient
*(Vt1)2 = h2+D2! * = distance FD2
soit t12 = (h2 + D2)/ V2.!!
De la même façon, si on considère le triangle rectangle CF'D,
le théorème de Pythagore permet d'écrire : F'D2 =CF'2+CD2.
En remarquant que FB+BD (trajet des ondes PMP) = F'B+BD!
et en remplaçant par leurs valeurs les diverses expressions, on
obtient!:
(Vt2)2 = (2H-h)2+D2! soit t22=(2H-h)2+D2/V2.
La suite du calcul est donnée ci-contre sachant que dt = t2-t1:
Calcul de la position du point de réflexion (distance AB)!:
Le théorème de Thalès appliqué au triangle F'CD permet
d'écrire l'égalité des rapports ci-contre :!
Il ne vous reste plus qu’à appliquer la 1ère formule pour connaître la profondeur du Moho et la 2de pour
connaître la position du point de réflexion.
Après avoir effectué le calcul, à la main et calculette pour le 1er exemple, afin de bien comprendre le
principe, pour les suivants, utilisez le tableau Excel appelé!: «!Calculs de la profondeur du Moho!» joint
à l’article.

 Exercice 5 page 160. + fiche exercice. (voir rubrique correction)
2. Résultats!: l’épaisseur de la croûte continentale.
Correction exercice 11 page 162
- Sous les Alpes!: (profil Ecors)
On note bien la présence d’un épaississement crustale sous les Alpes. On notera que le Moho y est
discontinu (voir chapitre suivant)
Profondeur du Moho à l’échelle de la
planète!:
Profondeur moyenne sous les océans!: 10
Km
Profondeur moyenne sous les
continents!: 30 Km
Zones de profondeur
- Très élevée!: Sous les chaînes de
montagnes
- Moyenne!: Centre des plaques
continentales
- Moins élevée!: Plateaux continentaux
30 Km
50 Km

PB!: comment expliquer les anomalies gravimétriques négatives sont localisées dans les zones
d’épaisseur maximale!?
3. La densité de la croûte continentale.
 Nous avons évalué en TP la densité des roches caractéristiques (Doc page 147)
Du manteau
péridotite
3,3
De la croûte océanique
Gabbro
3
De la croûte continentale
Granite
2,5
Ainsi l’excès de masse induit par la racine crustale est compensé par la plus faible densité de la croûte
continentale.
Comment expliquer ces différences de densité!?
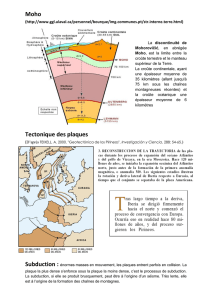
Plateau
Talus
D o m a i n e c o n t i n e n t a l
D o m a i n e o c é a n i q u e
Croûte continentale
croûte océanique
Lithosphère continentale (100 km)
L i t h o s p h è r e
Manteau lithosphérique
Asthénosphère -570 km-
Roche!: péridotite
Densité!: 3,3
Roche!: granite
Densité!: 2,6
Roche!: gabbro
Densité!: 3
Moho
LVZ