I Partie

CEA 16 Juin 2006
I Partie
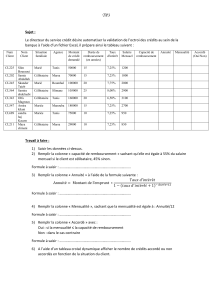
On étudie un crédit immobilier portant sur 300 000€ remboursable par mensualités
constantes payables à terme échu.
Pour toutes les formules étudier on retient un taux mensuel de im = 0.35%
1°) Calculer la mensualité pour des remboursements en 15 ans, 20 ans et 25 ans
im = 0.35%
k=12
n= 15, 20, 25
Avec a = annuité, i = taux d’intérêt annuel, V0 =Valeur actuelle, n = nombre d’annuité
constantes versées en fin de période
Suite géométrique de raison  

Calcul de l’annuité constante payable en fin de
période 
durée
15
20
25
capital initial
300000
300000
300000
taux nominal
4.20%
4.20%
4.20%
taux proportionnel
0.35%
0.35%
0.35%
nombre de périodes
12
12
12
annuités constantes
27361.03
22467.23
19611.67
périodicité constante
2249.25
1849.71
1616.83
2°) Pour chaque durée, 15 ans, 20 ans et 25 ans, Calcul le montant des
intérêts payés ainsi que le montant des intérêts payés au titre de la 10° année
de remboursement
Intérêts total payer IT pour l’emprunt

Le paiement périodique s’écrit
L’amortissement périodique de capital s’écrit
durée
15
20
25
capital initial
300 000.00
300 000.00
300 000.00
taux nominal
4.20%
4.20%
4.20%
taux proportionnel
0.35%
0.35%
0.35%
nombre de périodes
12
12
12
annuités constantes
27 361.03
22 467.23
19 611.67
périodicité constante
2 249.25
1 849.71
1 616.83
Intéréts totaux
104 865.19
143 930.93
185 048.09
intérêts 10 année
5 594.39
7 928.36
9 288.79

Intérêts cumulé payer ITp pour l’emprunt après le p° paiement
Le paiement périodique s’écrit
L’amortissement périodique de capital s’écrit
Calcul du capital remboursé Rp après le paiement du Pieme remboursement

durée
15
20
25
capital initial
300 000.00
300 000.00
300 000.00
taux nominal
4.20%
4.20%
4.20%
taux proportionnel
0.35%
0.35%
0.35%
nombre de périodes
12
12
12
annuités constantes
27 361.03
22 467.23
19 611.67
périodicité constante
2 249.25
1 849.71
1 616.83
Intéréts totaux
104 865.19
143 930.93
185 048.09
intérêts 10 année
5 594.39
7 928.36
9 288.79
IT9
85 851.44
95 029.44
100 379.15
IT10
91 445.83
102 957.79
109 667.95