Pour une fonction

BEP date :
Ph. Georges Maths 1/3
Error!
Error!
(C)
x
O
FONCTIONS et COURBES REPRÉSENTATIVES
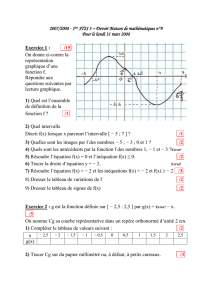
Quelques rappels pour distinguer par la suite les fonctions et de leurs courbes représentatives.
Il s'agit entre autre de ne pas confondre l'écriture d'une fonction numérique et celle de l'équation de sa
courbe représentative.
 Une fonction numérique transforme un nombre réel en un et un seul autre nombre réel par une
combinaison d'opérations.
Le nombre réel qui subit la transformation est appelé la variable.
Par exemple, la fonction numérique f fait correspondre à la variable x (ou n'importe quel
symbole) un nombre réel f(x), l'image de x par f.
La fonction f peut être définie :
- par son expression algébrique f(x) = … ou f : x
Error!
… ;
- par la connaissance de l'image pour certaines valeurs de la variable ;
Ces valeurs regroupées un tableau constituent un tableau de valeurs.
- par sa représentation graphique;
 La courbe représentative d'une fonction numérique f est l'association des couples (x, f(x)) a des points
du plan.
Dans le plan rapporté à un repère (O;
Error!
,
Error!
) d'axes x'Ox et y'Oy, l'ensemble des points M,
dont les coordonnées sont x et y = f(x) constitue la représentation graphique de la fonction f.
La relation y = f(x) est appelée équation de la courbe représentative de la fonction f.
Remarque 1 : on peut écrire :
Error!
= x
Error!
+ f(x)
Error!
dans un repère (O;
Error!
,
Error!
).
Remarque 2 : Toutes les courbes ne sont pas des représentations de fonctions numériques.
Exemple : A la variable x correspond 2 images.
(C) n'est pas une représentation d'une fonction numérique.

BEP date :
Ph. Georges Maths 2/3

BEP date :
Ph. Georges Maths 3/3
Propriétés et vocabulaire associés à une fonction ou à une courbe
Pour une fonction
On étudie ses variations.
Elle peut être croissante, décroissante ou
constante sur un intervalle.
Une fonction peut admettre un extremum,
(maximum ou minimum).
Une fonction peut être paire, impaire ou ni
paire ni impaire.
Une fonction peut être périodique.
Pour une courbe
Une courbe peut être représentative d'une
fonction
Une courbe peut admettre des équations.
L'équation réduite est de la forme y = f(x).
Une courbe est une droite, une parabole, une
hyperbole, une sinusoïde, etc.
Une courbe peut être parallèle, perpendiculaire
ou orthogonale.
Minimum et maximum d'une fonction
On considère une fonction numérique f définie sur [a;b].
f(xM) est une valeur maximum de la fonction f sur [a;b] si f(xM) f(x) pour tout x de [a;b].
f(xm) est une valeur minimum de la fonction f sur [a;b] si f(xm) f(x) pour tout x de [a;b].
Exemple:
Propriétés des fonctions
1- Fonction paire - Fonction impaire
Une fonction f définie sur un intervalle est paire si, pour tout x de cet intervalle, (-x)
appartient à cet intervalle et f( – x) = f(x).
Une fonction f définie sur un intervalle est impaire si, pour tout x de cet intervalle, (-x)
appartient à cet intervalle et f(– x) = – f(x).
Conséquence graphique:
La représentation graphique d'une fonction paire admet l'axe Oy comme axe de symétrie.
La représentation graphique d'une fonction impaire admet le point O(0,0) comme centre
de symétrie.
2- Fonction périodique
Une fonction f est périodique de période T si, quel que soit le nombre x, f(x) = f(x + T).
Conséquence graphique:
La représentation graphique d'une fonction périodique se complète.
f(xm)
f(xM)
b
a
x
y