Dérivation de la Courbe de Phillips Néo-Keynésienne Hybride

Dérivation de la Courbe de Phillips
Néo-Keynésienne Hybride∗
Abel KUTANGILA Lufutu†
Contact: kutangila.ab[email protected]
Web: http://www.lareq.com
27 avril 2015
Résumé
After several controversies, the famous Phillips curve left then from
its initial version, to the advanced Phillips curve (of anticipations), to
the Neo-keynesian Phillips Curve (NKPC) and finally to the hybrid neo-
keynesian Phillips curve. Derived of the explicit microeconomic founda-
tions on the optimal behavior of the economic agents, the present versions
of the Phillips curve have succeeded to avoid of the Lucas critique. They
often served to the reproduction as well of the inflation dynamics as of
the empiric persistence in inflation.
Keywords : Neo-keynesian Phillips Curve, Degree of persistence in
inflation, inflation dynamics
Introduction
Toutes les politiques économiques contemporaines reposent implicitement ou ex-
plicitement sur une formulation issue de l’analyse keynésienne (ou d’une critique
de celle-ci ; il s’agit d’un point de vue indiscutable (Abrahama-Frois, 1986).
Deux objectifs essentiels des politiques économiques sont un faible niveau d’in-
flation et un chômage réduit, mais ces deux objectifs sont souvent conflictuels
(Mankiw, 2005). L’inflation étant procyclique et le chômage contracyclique,
cette incompatibilité rend difficile la maîtrise simultanée de ces deux maux.
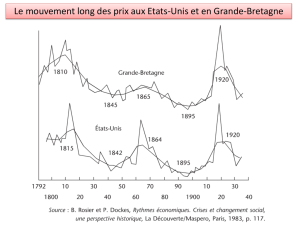
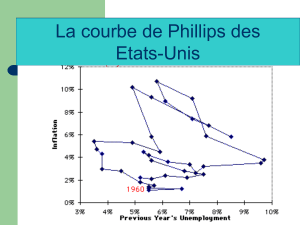
La célèbre courbe dite de Phillips, mettant en dualité le taux de chômage et
celui d’inflation, renseigne de l’existence, en période croissance, d’une relation
négative entre les deux agrégats macroéconomiques. Précisément quand le chô-
mage est faible l’inflation est forte et vice-versa ; il peut même arriver le cas où
l’inflation est négative : c’est la déflation.
∗ONE PAGER LAREQ 2015. Web: http://www.lareq.com/one-pager-lareq.ws
†Chercheur au Laboratoire d’analyse-recherche en économie quantitative.
1

La courbe de Phillips est certainement la plus controversée en économie, car
son examen pour différents pays révèle l’instabilité de la relation empirique
entre inflation et chômage. Cependant, chaque remise en cause a donné lieu
à une reformulation, à telle enseigne que le concept de cette courbe demeure
central dans nombre d’analyses macroéconomiques, plus singulièrement dans le
domaine de politique monétaire.
La courbe de Phillips sous sa forme moderne est donc très éloignée de la for-
mulation initiale. On est parti de la courbe de Phillips à la courbe de Phil-
lips augmentée (des anticipations), puis à la courbe de Phillips néo-keynésienne
(NKPC) 1, qui a réussit de se soustraire de la critique de Lucas 2. Car, en ef-
fet, comme le note Le Bihan (2009), la NKPC est une relation entre l’inflation
et une variable réelle, obtenue dans le cadre d’un modèle théorique de fixation
optimale des prix par les entreprises dans un contexte inter-temporel.
Mais très vite, la version canonique de la nouvelle courbe de Phillips a aussi
révélé certaines faiblesses entre autres d’une part, l’inflation courante ne dépend
pas de l’inflation passée ; et d’autre part, l’inertie de l’inflation ne peut être due
qu’à celle de la variable explicative. Pour autoriser plus de persistance, un grand
nombre de travaux (Gali et Gertler (1999),. . .) ont obtenu la courbe de Phillips
hybride qui, elle, introduit de la persistance et permet de rendre compte de
la dynamique inertielle de l’inflation après un choc. C’est donc cette dernière
version qui fait l’objet de ce papier.
Encadré d’une introduction et d’une conclusion, ce papier gravite autour de
quatre sections. La première section fixe les hypothèses qui sous-tendent la dé-
rivation de la courbe de Phillips hybride. Les trois autres sections exploitent
respectivement en détail la concurrence monopolistique, la rigidité des Prix avec
le modèle de Calvo ainsi que le modèle de Gali et Gertler.
Hypothèses de base du modèle
La Macro Néo-Keynésienne cherche principalement à développer un cadre d’ana-
lyse macroéconomique qui est basé sur les concepts néoclassiques de maximi-
sation de la fonction objectif et des anticipations rationnelles. Mais dans cette
maximisation, il est incorporé l’hypothèse keynésienne selon laquelle les prix
sont rigides à court terme à cause des coûts d’ajustement, mais aussi de l’im-
perfection de l’information.
1. La NKPC est apparue au milieu des années 1990 dans les travaux d’analyse de la poli-
tique monétaire et a été popularisée par Gali et Gertler (1999)
2. Lucas postule que les agents forment leurs anticipations en tenant compte de toute infor-
mation disponible afin de ne pas commettre des erreurs de prévision : ils font des anticipations
rationnelles. Il vient que leur comportement peut être soudainement affecté par des change-
ments d’environnement économique (politiques économiques), ce qui est de nature à affecter
les anticipations. Les anticipations faites de manière prédéterminée ne devraient donc pas être
employées dans l’évaluation des politiques économiques alternatives.
2

La courbe de Phillips néo-keynésienne est une relation entre l’inflation et l’ac-
tivité réelle (il s’agit ici de l’output gap, c’est-à-dire l’écart de la production).
Elle est obtenue dans le cadre d’un modèle théorique de fixation optimale des
prix par les entreprises dans un contexte inter-temporel. A l’égard des modes
de fixation des prix, elle renseigne sur le comportement d’agents.
Trois hypothèses sont faites pour obtenir la courbe de Phillips Néo-keynésienne
hybride, savoir :
H1 : L’entreprise évolue dans un environnement de concurrence monopolistique
et dispose, de ce fait, d’un pouvoir de fixation des prix.
H2 : Les prix sont rigides : l’entreprise ne peut ajuster le prix au niveau désiré
à toutes les dates. L’ajustement des prix se fait de manière non fréquente et
non simultanée dans l’économie.
H3 : Les entreprises fondent leurs décisions sur des anticipations rationnelles.
Nous pouvons à présent, analyser plus ou moins profondément chaque hypo-
thèse.
Concurrence monopolistique
Le point de départ de la mise en évidence de la NKPC c’est un environne-
ment de concurrence imparfaite. Il est de bon aloi, avant d’aller plus loin, de
rappeler avec Médan (1999) qu’un marché est un concurrence monopolistique
lorsqu’il comporte un grand nombre de vendeurs dont les produits sont diffé-
rentiés et qu’il y a libre entrée. Pour des raisons liées à la qualité des produits,
à la publicité, ou encore à la localisation, la firme détient une clientèle captive :
elle possède un certain pouvoir de monopole. par conséquent, la demande qui
s’adresse à la firme est plus ou moins décroissante ; elle n’est donc plus égale,
comme en monopole pur, à la demande du marché. La concurrence monopo-
listique rassemble les éléments de la concurrence pure et parfaite (qui existent
surtout en longue période) et des éléments de monopole (qui existent surtout
en courte période).
La concurrence monopolistique est le type de marché le plus souvent rencontré
dans les cas pratiques, mais dont l’analyse n’est pas aisée à réaliser. Si nous
considérons que l’entreprise évolue dans un environnement de concurrence mo-
nopolistique, on s’accorde alors qu’elle dispose d’un pouvoir de fixation de prix.
Dans ce cas, le prix devient une variable d’ajustement pour la firme. Contrai-
rement aux modèles de concurrence parfaite où la firme agit sur les quantités
vendues et considère le prix du produit comme une donnée, ici les firmes sont
price-maker.
Les ménages
Considérons le modèle de Blanchard et Kiyotaki (1987), est un modèle standard
de concurrence monopolistique au sein de la littérature néo-keynésienne. Ici
3

l’environnement de concurrence imparfaite se base sur l’hypothèse selon laquelle
les ménages s’intéressent à la consommation de produits différenciés et que les
firmes choisissent leur prix afin d’optimiser les profits. Supposons singulièrement
que l’index de consommation agrégée ctsoit composé d’un continuum de biens et
services de consommation ct(z), avec z∈[0,1]. Ainsi, l’index de consommation
agrégée ct, formé par l’ensemble des zbiens est donné par :
ct=Z1
0
ct(z)(µ−1)
µdz
µ
µ−1
(1)
où µ1est un paramètre interprété comme l’élasticité de substitution (constante)
entre les biens différenciés. Dans ce cas, on s’approche de la compétition parfaite
à mesure que µest proche de 1.
Puisque les consommateurs sont tournés vers l’objectif de minimisation de coût
(de consommation), il vient qu’à l’optimum la demande ct(z)du consommateur
pour le z-ième bien est donnée :
ct(z) = Pt(z)
Pt−µ
ct(2)
où Pt(z)est la prix du produit zet Ptle prix de l’index de consommation
agrégée ctqu’on peut dériver comme
Pt≡Z1
0
Pt(z)1−µdz
1
1−µ
.(3)
D’autre part, nous supposons, comme il en est le cas dans une économie de
marché et de propriété privée, que tous les facteurs de production sont détenus
par les ménages, qui les font louer aux firmes. Les ménages peuvent également
détenir les droits de propriété sur les firmes. Ceci est matérialisé principalement
par l’attribution des droit de propriété qu’ils détiennent. La valeur de ces profits
est mesurée en termes d’utilité marginale de la consommation que chaque unité
de profit apporte.
Les firmes
Revenus et coûts des firmes
Toute firme poursuit la maximisation des revenus qui passe par la maximisation
de ses recettes d’une part et la minimisation de ses coûts 3d’autre part.
Supposons que la fonction de coût nominal de la firme soit donnée par Φt(ct(z)),
où l’indice tde Φindique la présence des facteurs autres que ct(z)susceptibles
3. Font partie des coûts de la firme : la rémunération de la main d’œuvre, les coûts de
capital et le paiement de tout autre facteur de production (énergie et matériaux)
4

d’effecter les coûts de la firme. Dans ce cas, la fonction de coût réel sera donnée
par le rapport φ(ct(z)) = Φ(ct(z))/Pt. Ainsi, les profits réels de la firme zsont
donnés par la différence entre ses recettes et ses coûts réels :
qt(z) = Pt(z)
Pt
ct−φ(ct(z))(4)
Connaissant le coût nominal et le coût réel de la firme z, nous pouvons déjà à
ce niveau en déterminer respectivement les expressions des coûts marginaux y
relatifs tels que :
Ψt(z) = ∂Φ(ct(z))
∂ct(z)et ψt(z) = ∂φ(ct(z)) ∂ct(z)(5)
Détermination du prix optimal
Partant de l’hypothèse d’une flexibilité parfaite des prix, nous considérons qu’après
avoir pris connaissance de l’état de la demande et des coûts, le prix nominal peut
être établi sans coût à chaque période.
Par ailleurs, connaissant que le programme du producteur du bien zse résume
dans la maximisation des profits, il s’ensuit que si le monopoleur veut maximiser
ses profits réels q(.), il fixe le prix nominal en respectant les conditions de premier
ordre qui établissent que le prix qui maximise les profits réels sera obtenu en
annulant la dérivée première des profits réels par rapport au prix de ce bien.
Formellement
∂qt(ct(z))
∂Pt(z)=1 Pt
ct+Pt(z)
Pt
∂ct(z)
∂Pt(z)−∂φt(ct(z)) ∂ct(z)
∂ct(z)
∂Pt(z)= 0.(6)
Après manipulation de cette équation, il s’établit que les conditions d’efficience
du monopoleur égalise le revenu marginal aux conséquences sur les coûts :
1
Pt
ct(z) + Pt(z)
Pt
∂ct(z)
∂Pt(z)=ψt(z)∂ct(z) ∂Pt(z).(7)
La fonction de la demande pour le z-ième bien est connue, et donnée par l’équa-
tion (2). On peut donc l’insérer dans l’expression (7) pour avoir, après résolution,
la fonction du prix relatif que le monopoleur – qui fait face à une courbe d’élas-
ticité constante – détermine comme une marge ajoutée fixe sur le coût marginal
réel à chaque période tdu temps. C’est ce qu’établissent Blanchard et Kiyotaki
(1987) :
Pt(z)
Pt
=µ
µ−1ψt(z)(8)
avec µ/(µ−1) la taille de cette marge ajoutée fixe qui doit toujours être positive
car dépendant de l’élasticité de la demande µ1.
5