Retour à l`applet Expérience de Millikan Retour à l`applet

Retour à l’applet
Expérience de Millikan
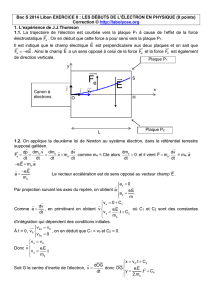
Avec un pulvérisateur, on insuffle des gouttelettes d’huile entre les armatures d’un
condensateur plan horizontal. La distance entre les armatures est d = 1 cm. La différence de
potentiel V entre ces armatures est réglable entre 0 et 300 V. Le module du champ électrique
E est donc égal à Vd. Le champ, vertical, est dirigé vers le haut. Les gouttelettes sont chargées
soit par frottement sur le bec du pulvérisateur soit avec une source ionisante. Chaque
gouttelette de rayon a en mouvement est soumise à :
Son poids ga
3
4
gmP3rr
r
ρπ== (avec ρ = 800 kg.m–3).
La poussée d’Archimède g'a
3
4
'P3r
r
ρπ−= (avec ρ’ = 1,29 kg. m–3).
Le frottement du à l’air av6F1πη−=
r
(avec η = 1,8.10–5 Nsm–2)
La force électrique EqF2
r
r
= q = k.1,6.10–19 C (k entier)
En agissant sur la valeur de V, il est possible d’immobiliser des gouttelettes chargées
négativement.
Le principe de la dynamique appliqué à une gouttelette en mouvement donne :
av6qEga
3
4
dt
dv
m3πη−−ρπ=
qui admet comme solution :
−
πη
−ρπ
=ηπ−m
ta6
3
e1
a6
qEga
3
4
v
Compte-tenu de la valeur du coefficient de t dans l’exponentielle, on arrive très vite à la
vitesse limite a6qEga
v3
3
4
πη −ρπ
=
Si le champ est nul, la mesure de la vitesse de chute ηρ= 9/ga2v2 permet de déduire a.
Si la goutte est immobile, on tire : gaqE 3
3
4ρπ= et donc : E/va6q
πη
=
Pour mesurer la charge d’une goutte, on l’immobilise en ajustant V puis on annule la ddp et
on mesure la durée de chute sur une distance connue ce qui permet d’obtenir la valeur de v.
Pratiquement, on utilise le réticule gradué du viseur d’observation des gouttelettes.
(Observation sur un fond sombre avec un éclairage latéral).
L’applet proposée simule cette expérience en créant des gouttelettes de rayons a et de charges
ke avec des valeurs aléatoires pour k (entier négatif ou nul) et pour a. Toutefois, la majorité
des valeurs de a générées permet d’immobilisation de la goutte choisie.
Retour à l’applet