8 - Modélisation et Méthodes Mathématiques

Analyse Mathématique
Exercice proposé du 8/10/1999.
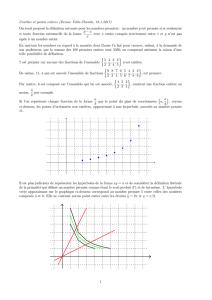
Montrer que les hyperboles
222 axy =− et 2
bxy =
se coupent à angle droit quelles que soient les constantes a et b.
Solution :
On peut résoudre cet exercice de deux manières différentes.
Première méthode
Recherchons le(s) point(s) d’intersection des deux hyperboles et montrons que les tangentes à chacune des
courbes sont perpendiculaires en ce(s) point(s)
Résolvons le système suivant : 
=−
=(1) (2)
222
2axy bxy
⇔ 0 si
2
2
4
2
2≠
=−
=y
a
y
b
y
y
b
x
⇔ 0 si
0
4224
2
2≠
=−−
=y
byay
x
b
x
0 si
0
22
2=
=− =y
ax
b
0 si
0
0==
=
=ba
x
y
⇒
2
4442
2baa
y+± =
Comme 0
2≥y, on doit retenir la solution
2
4442
2baa
y++ =
⇒ 24442
0baa
y++ =ou 24442
0baa
y++ −=
⇒ 444
4422
442
2
04
4.2
4
.2
aba
baab
baa
b
x−+ ++− =
++
=ou 442
2
04
.2
baa
b
x++
−
=
24442
0baa
x++− =ou 24442
0baa
x++− −=

Si les deux courbes sont perpendiculaires en un point, le produit des coefficients angulaires de leur tangente
respective en ce point vaut
1
−
⇒ 22
1xay+±=
⇒ 22
'
12
2
xa
x
y+ ±=
et
442
444
442
442442
442
442
0
'
14
4
4
)4)(4(
2
4
24
)( baa
aba
baa
baabaa
baa
baa
xy ++ −+
=
++
++++−
=
++
++−
±
±=
les signes
±
se correspondent car 2 bxy = ⇒
x
et
y
sont de même signe.
442
2
0
'
14
2
)( baa
b
xy ++ =
(2) ⇒
x
b
y2
2=
⇒ 2
2
'
2
x
b
y− =
et 442
2
0
'
24
2.
)( baa
b
xy ++− − =
Il vient ensuite,
1
44
)4)(4(
4
)().(444
4
442442
4
0
'
20
'
1−=
−+−
=
++++− −
=aba b
baabaa
b
xyxy CQFD
Si 0
=
x,les hyperboles deviennent
a
y
±
=
et 0
=
b. On a donc deux droites, chacune étant parallèle
à un axe de coordonnée. Elles sont donc perpendiculaires.
Si 0
=
y,les hyperboles deviennent 
=−=
22
0ax b ⇒ 0
=
a et donc 0
=
=
yx .
Les deux hyperboles se réduisent alors à un point et le problème n’a plus beaucoup de sens.

Deuxième méthode
Les relations
=− =(1) )( (2) )(
22
11
2
12
222
axxy bxyx
définissent implicitement les fonctions )( 111 xyy = et )( 222 xyy =. Par dérivation, on obtient :
=− =+ 02)(20)()( 1
'
111
2
'
2222
xyxy xyxxy
De là,
=
−
=
1
1
1
'
1
2
2
2
'
2
)(
)(
y
x
xy
xy
xy
Le vecteur directeur de la tangente à une courbe est donné par ))(,1())(,(''' xyxyx =
1. on obtient
−
(1)pour ),1(
(2)pour ),1(
1
1
2
2
y
x
xy
Si les deux tangentes sont perpendiculaires, le produit scalaire de leur vecteur directeur est nul.
Ici, on a : 01
2
2
1
1=− x
y
y
x pour les points d’intersection car dans ce cas,
=
=21
21
xx yy
et les deux hyperboles se coupent bien perpendiculairement.