chapitre 3 : droites remarquables du triangle

Mathé matiques Niveau 1 et 2 Troisième partie Fonctions
Collège Sismondi (S.Z., cours G.E.) 2007 - 2008 chap.3, p.1
CHAPITRE 3 :
CHAPITRE 3 :
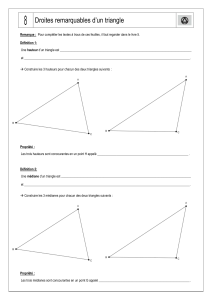
DROITES REMARQUABLES DU TRIANGLE
DROITES REMARQUABLES DU TRIANGLE
§ 3.1 Les médiatrices
Définition
La médiatrice d'un segment de droite est l'ensemble des points situés à égale distance des
extrémités de ce segment.
Cela signifie que si X est un point de la médiatrice du segment AB, alors δ(A,X) = δ(B,X).
On peut démontrer que la médiatrice d'un segment est une droite perpendiculaire à ce segment et passant
par son milieu.
En effet, si A et B sont les extrémités du segment et M son
point milieu, il est évident que M appartient à la médiatrice de
AB. Si maintenant X est un autre point de la médiatrice de AB,
alors X est tel que δ(A,X) = δ(B,X). Mais alors le triangle ABX
est isocèle et selon ce qui a été démontré à la fin du chapitre
précédent, la droite MX est perpendiculaire à la droite AB.
Donc tous les points de la médiatrice de AB sont situés sur
une droite passant par M et perpendiculaire au segment AB.
A
B
X
M
Théorème
Les trois médiatrice d'un triangle se coupent en un même point.
Démonstration
Appelons D le point d'intersection des médiatrices de AB et BC et montrons que D est un point de la
médiatrice de AC.
A
B
C
médiatrice de BC
médiatrice de AB
D

Mathé matiques Niveau 1 et 2 Troisième partie Fonctions
Collège Sismondi (S.Z., cours G.E.) 2007 - 2008 chap.3, p.2
Par définition, δ(A,D) = δ(B,D) et δ(B,D) = δ(C,D), donc δ(A,D) = δ(C,D), ce qui montre que D (étant à
la même distance de A et de C) appartient à la médiatrice de AC, donc que les trois médiatrices se
coupent en un même point (le point D).
De plus, comme D est à égale distance des trois sommets du triangle, un cercle centré en D et passant par
l'un des sommets passe aussi par les autres sommets.
E
F
G
C
médiatrice de EF
médiatrice de EG
Le point d'intersection des médiatrices d'un triangle est le centre du cercle circonscrit au triangle.
§ 3.2 Les bissectrices
Définition
La bissectrice d'un angle est l'ensemble des points situés à égale distance des deux demi-droites
délimitant cet angle.
Cela signifie que si X est un point de la bissectrice de l'angle formé par les demi-droites d1 et d2,
alors δ(d1,X) = δ(d2,X).
On peut démontrer que la bissectrice d'un angle est une droite qui divise l'angle en deux parties égales.
En effet, il est évident que le sommet de l'angle est
un point de la bissectrice (car ce point est sur les
deux droites, donc à la même distance de chacune
d'elles !). Si maintenant X est un autre point de la
bissectrice de l'angle formé par les demi-droites d1
et d2, alors δ(d1,X) = δ(d2,X). Mais dans ce cas, les
triangles SQX et SPX sont rectangles et
QX =PX
S
P
Q
X
d2
d1
2
!1
!
Alors, selon le théorème de Pythagore,
SQ2=SX2!XQ2=SX2!XP2=SP2
, c’est-à-dire
SQ =SP
.
Ceci montre que les triangles SQX et SPX sont égaux et qu'ils ont les mêmes angles, donc α1 = α2.
La bissectrice partage donc l'angle en deux parties égales.

Mathé matiques Niveau 1 et 2 Troisième partie Fonctions
Collège Sismondi (S.Z., cours G.E.) 2007 - 2008 chap.3, p.3
Théorème
Les trois bissectrices d'un triangle se coupent en un même point.
Démonstration
Appelons D le point d'intersection des bissectrices de α et β, et montrons que D est un point de la
bissectrice de γ.
A
C
B
D
d1
d3
d2
bissectrice de
bissectrice de
!
"
Par définition, δ(d2,D) = δ(d3,D) et δ(d1,D) = δ(d3,D), donc δ(d1,D) = δ(d2,D) ce qui montre que D
(étant à la même distance de d1 et de d2 ) est un point de la bissectrice de γ, donc que les trois
bissectrices se coupent en un même point (le point D).
De plus, comme D est à égale distance des trois côtés, un cercle centré en D tangent à l'un des côtés est
tangent aux autres côtés.
A
B
C
bissectrice de
bissectrice de
!
"
GG est le centre du cercle inscrit
Le point d'intersection des bissectrices d'un triangle est le centre du cercle inscrit du triangle.

Mathé matiques Niveau 1 et 2 Troisième partie Fonctions
Collège Sismondi (S.Z., cours G.E.) 2007 - 2008 chap.3, p.4
§ 3.3 Les hauteurs
Définition
Une hauteur d'un triangle est une droite issue d'un sommet et perpendiculaire à la droite contenant le
côté opposé.
Théorème
Les trois hauteurs d'un triangle se coupent en un même point.
Démonstration
Par chacun des sommets du triangle ABC, on fait passer une droite parallèle au côté opposé. On
obtient ainsi un nouveau triangle A'B'C'.
C
B
A
A'
B'
C'
hauteur issue de A
Par construction, le quadrilatère ACBC' est un parallèlogramme, donc
CB =AC'
; de la même façon
CB =B' A
: ceci montre que le sommet A est au milieu du côté B'C'. Comme les côtés BC et B'C' sont
parallèles, la hauteur issue de A (dans le triangle ABC) est la médiatrice du côté B'C' (dans le triangle
A'B'C'). Donc les hauteurs du triangle ABC sont les médiatrices du triangle A'B'C'. Mais nous savons
que les médiatrices (du triangle A'B'C') se coupent en un même point, donc nous pouvons conclure
que les hauteurs (du triangle ABC) se coupent en un même point.
Remarque :
Le terme hauteur est utilisé dans deux sens différents : d'une part c'est la droite issue d'un sommet et
perpendiculaire à la droite contenant le côté opposé et d'autre part, c'est la distance du sommet à la
droite contenant le côté opposé (c'est cette distance que l'on utilise pour déterminer l'aire d'un
triangle). Le contexte suffit en général à préciser de quelle "hauteur" il s'agit.

Mathé matiques Niveau 1 et 2 Troisième partie Fonctions
Collège Sismondi (S.Z., cours G.E.) 2007 - 2008 chap.3, p.5
§ 3.4 Les médianes
Définition
Une médiane d'un triangle est une droite issue d'un sommet et passant par le milieu du côté opposé.
Théorème
Les trois médianes d'un triangle se coupent en un même point.
Démonstration
Soit le triangle ABC et les points M, N et P
respectivement milieux des segments AB, BC et
AC.
On a donc
BM
BA =1 2
et
BN
BC =1 2
, ce qui montre
que les droites MN et AC sont parallèles.
Soit maintenant R le point d'intersection des
droites BP et MN.
A
B
C
M
N
P
R
Selon Thalès,
MR
AP =BM BA =1 2
, donc
MR =1
2AP
et de la même façon
NR =1
2PC
; mais comme
AP =PC
, il en résulte que
MR =NR
et que R est le milieu de MN. La médiane BP du triangle ABC
est aussi médiane du triangle MNP.
Imaginons maintenant une suite infinie de triangles
construits de la façon suivante : les sommets d'un
triangle sont les milieux des côtés du triangle
précédent.
D'après ce qui précède, les médianes du premier
triangle sont aussi les médianes des autres ! Et
comme les triangles sont toujours plus petits, il n'y
a pas la place à l'intérieur de ces triangles pour plus
qu'un point. Ce qui montre que les médianes du
triangle de départ ne peuvent pas se rencontrer
autrement qu'en un point.
A
B
C
M
N
P
R
T
S