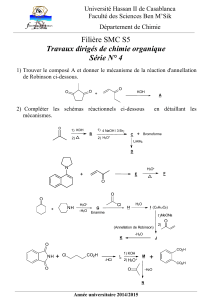
04/10/00 1ère S - cours

Oct 2014 TS Devoir de physique–chimie n°1 (1 h environ) NOM : ……………………………..
FAIRE DES PHRASES POUR REPONDRE
CHIMIE : Le venin des fourmis /20,0 CALCULATRICE AUTORISEE
Données :
Produit ionique de l’eau : Ke = 1,0.10–14 dans les conditions de l’expérience. pKa(HCOOH/HCOO–) = 3,75.
Masses molaires : M(H) = 1,0 g.mol–1 ; M(C) = 12,0 g.mol–1 ; M(N) = 14,0 g.mol–1 ; M(O) = 16,0 g.mol–1 ;
Pour se défendre les fourmis utilisent deux moyens : leurs mandibules et la projection d’acide formique. Les mandibules servent à immobiliser l’ennemi tandis que l’acide formique brûle la victime. Une
fourmi se sentant menacée se dresse sur ses deux pattes arrières et peut projeter sur l’ennemi un jet d’acide formique à plus de 30 centimètres grâce à son abdomen. L’acide formique (ou acide méthanoïque)
a pour formule semi développée HCOOH. Il réagit avec l’eau selon l’équation suivante : HCOOH(l) + H2O(l) HCOO–
(aq) + H3O+ (aq)
En laboratoire, il existe une solution d'acide formique S0 de concentration C0 = 0,20 mol.L–1. Une solution d'acide formique S1 de concentration C1 = 1,0.10–2 mol.L–1 est préparée à partir de la
solution S0. Cette solution S1 a une concentration en ion oxonium [H3O+]f = 1,3.10–3 mol.L–1.
A. Préparation de la solution
A.1. Donner le protocole expérimental pour former 100,0 mL de solution S1 à partir
de la solution S0.
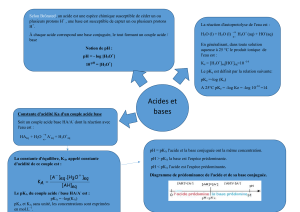
A.2. Donner les définitions d'un acide et d'une base dans la théorie de Bronsted.
A.3. Pour former 100 mL de la solution initiale d'acide formique S0 de concentration
C0, quelle quantité de matière d'acide formique n0(HCOOH) a été utilisée ?
B. Etude de l'acide formique
B.1. Calculer le pH de la solution S1.
B.2. Faire un diagramme de prédominance du couple acide méthanoïque/ion méthanoate.
En déduire l'espèce prédominante dans la solution S1.
B.3. Compléter de façon littérale le tableau d’avancement ci-dessous correspondant à
la transformation précédente (à faire sur la feuille d'énoncé)
HCOOH(l) + H2O(l) HCOO–(aq) + H3O+(aq)
État initial (x = 0)
État final (x = xf)
État si réaction
totale
(x = xmax)
B.4. Cette transformation est–elle totale ou limité ? Justifier par le calcul (xf et xmax)
B.5. L’acide formique est–il un acide fort ou un acide faible ? Justifier.
B.6. Calculer la concentration finale en ions hydroxyde.
B.7. Donner l’expression de la constante d’acidité du couple HCOOH(aq)/HCOO–(aq).
B.8. Démontrer que Ka = [H3O+]2
f
C1 – [H3O+]f
B.9. Sachant [H3O+]f = 1,3.10–3 mol.L–1, calculer la constante d'acidité du couple
étudié et retrouver la valeur du pKa de ce couple.
C. Neutralisation
Afin de neutraliser (rendre le pH neutre) les solutions S0 et S1, les 2 solutions sont mélangées et on
ajoute une certaine quantité de solution d'hydroxyde de sodium Na+ + HO–.
C.1. Ecrire l'équation de la réaction entre les solutions d'acide méthanoïque et
d'hydroxyde de sodium.
C.2. BONUS : Faire un schéma de l'expérience servant à la neutralisation (avec le matériel
permettant de contrôler précisément la neutralité de la solution finale).
D. Effet tampon
Le laborantin veut préparer une solution tampon avec le couple de l'acide méthanoïque
HCOOH(aq)/ HCOO–
(aq).
D.1. Qu'est ce qu'une solution tampon ?
D.2. Quelle doit être la composition de la solution tampon formée ?
D.3. Autour de quelle valeur le pH de la solution tampon former va se stabiliser ?

Correction DS 1
CHIMIE : Le venin des fourmis /20,0
A. Préparation de la solution 2+1,5+1,5 = 5,0
A.1. C0
C1 = 0,20 1,0.10–2 = 20 La solution S0 est diluée par un facteur 20 pour faire la solution S1.
Si on veut préparer 100,0 mL de S1, il faut prélever donc 5,0 mL de S0 (100,0
5,0 = 20)
Protocole expérimental de la préparation de la solution S1 :
Prélever 5,0 mL de la solution S0 avec une pipette jaugée de 5,0 mL.
Verser ce prélèvement dans une fiole jaugée de 100 mL.
Ajouter de l'eau distillée jusqu'au trait de jauge (attention au ménisque).
Boucher et agiter pour homogénéiser.
A.2. Un acide est une espèce capable de céder un proton H+.
Une base est une espèce capable de capter un proton H+.
A.3. C0 = n0(HCOOH)
V n0(HCCOH) = C0.V = 0,20 x 100.10–3 = 2,0.10–2 mol
B. Etude de l'acide formique 0,5+1,5+2+1,5+0,5+1,5+1+1,5+1,5 = 11,5
B.1. pH = –log [H3O+]f = –log 1,3.10–3 = 2,9
B.2.
A pH = 2,9, l'acide formique (ou acide méthanoïque) est prédominant dans S1 (pH <pKa).
B.3.
B.4. 1ère méthode :
xf = nf(H3O+) = [H3O+]f.V = 1,3.10–5 x 100.10–3 = 1,3.10–6 mol
Si la réaction est totale, n0(HCCOH) – xmax = 0
donc xmax = n0(HCOOH) = C1.V = 1,0.10–2 x 100.10–3 = 1,0.10–3 mol
On a donc xf << xmax donc la réaction est limitée
2ème méthode :
Si la réaction était totale, n0(HCCOH) – xmax = 0 donc xmax = n0(HCOOH)
D'autre part, nmax(H3O+) = xmax donc nmax(H3O+)
V = xmax V= n0(HCOOH) V
On obtient donc [H3O+]max = C1 = 1,0.10–2 mol.L–1
On a ainsi [H3O+]f << [H3O+]max donc la réaction est limitée.
3ème méthode :
[H3O+]f = 10–pH = 10–2,9 = 1,3.10–3 mol.L–1
Donc xf = nf(H3O+) = [H3O+]f .V = 1,3.10–3 x 100.10–3 = 1,3.10–4 mol
nf(HCOOH) = n0(HCOOH) – xf = 1,0.10–3 – 1,3.10–4 = 8,7.10–3 mol
Il reste de l'acide formique à la fin de la réaction donc la réaction est limitée.
B.5. La réaction de l'acide formique avec l'eau est limitée donc l'acide est faible.
B.6. Ke = [H3O+]f.[HO–]f donc [HO–]f = Ke
[H3O+]f = 1,0.10–14 1,3.10–3 = 7,7.10–12 mol.L–1
B.7. Ka = [HCOO–]f.[H3O+]f
[HCOOH]f
B.8. D'après le tableau d'avancement,
xf = nf(HCOO–) = nf(H3O+) donc [HCOO–]f = [H3O+]f
nf(HCOOH) = n0(HCOOH) – xf = n0(HCOOH) – nf(H3O+)
donc nf(HCOOH)
V = n0(HCOOH)
V – nf(H3O+)
V d'où [HCOO]f = C1(HCOOH) – [H3O+]f
On obtient ainsi : Ka = [HCOO–]f.[H3O+]f
[HCOOH]f = [H3O+]f.[H3O+]f C1(HCOOH) – [H3O+]f = [H3O+]2
f
C1 – [H3O+]f
B.9. D'après 1.9., Ka = [H3O+]2
f
C1 – [H3O+]f = (1,3.10–3)2 1,0.10–2 – 1,3.10–3 = 1,8.10–4
pKa = –log Ka = – log 1,8.10–4 = 3,7
C. Neutralisation 1 (+1,5) = 1 (+1,5)
C.1. HCOOH (aq) + HO–(aq) HCOO–(aq) + H2O(l)
C.2. cf. schéma ci–contre
D. Effet tampon 1+1+ 0,5 = 2,5
D.1. Une solution tampon est une
solution dont le pH varie peu par
un ajout modéré d'acide, de base
ou par une dilution modérée.
D.2. Pour qu'une solution soit
tamponnée, il faut qu'elle contienne
la même quantité d'acide et de base
conjuguée du couple soit
nf(HCOOH) = nf(HCOO–)
D.3. Le pH de la solution tampon va se
stabiliser autour du pKa du couple
soit autour de 3,75.
Équation
HCOOH(l) + H2O(l) HCOO–(aq) + H3O+(aq)
Etat initial (x = 0)
n0(HCOOH)
Solvant
0
0
Etat final (x = xf)
n0(HCOOH) – xf
Solvant
xf
xf
Etat si raaction est
totale (x = xmax)
n0(HCOOH) – xmax = 0
Solvant
xmax
xmax
pH
pKa
3,75
HCOOH prédominant
[HCOOH]f > [HCOO–]f
HCOO– prédominant
[HCOOH]f < [HCOO–]f
potence
Burette graduée
contenant la solution de
soude
pH–mètre relié à la
sonde pH–métrique
Agitateur magnétique
et turbulent
Becher contenant les
solutions S0 et S1.