Physique :

Série n°1 4
èmes
Maths Prof : B EN K AHLA J AWHER Page 1
4
ème
Maths & Sc.exp
Série d’exercices N°1
Le Condensateur – Dipôle RC
Cinétique chimique
Lycée S OUKRINE - T EBOULBA
Prof : B EN K AHLA J AWHER
Physique
PhysiquePhysique
Physique :
::
:
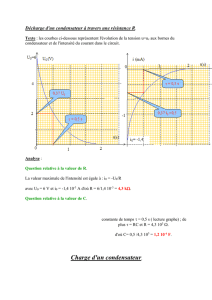
Exercice n°1:
1/ Compléter le montage ci-contre afin de charger le
condensateur de capacité C par un courant constant.
2/ Une carte d'acquisition et un logiciel permettent de tracer,
avec un ordinateur, la courbe u
AB
= f ( t ) suivante:
a) Déduire de la courbe si le condensateur est chargé ou déchargé au départ.
b) Comment varie la tension u
AB
en fonction du temps t dans ce cas?
c) Déterminer la relation entre u
AB
et t.
3/ a) Ici, le générateur est un générateur de courant constant. Ce générateur possède un débit constant
de charges électriques. On pose q
A
et q
B
les charges électriques acquises respectivement par les
armatures A et B a la date t.
Choisir les bonnes relations et corriger les autres : * q
B
= C.u
AB
* q
A
= C.u
AB
* q
A
= I.t *q
B
= I.t
.
b) Déterminer la valeur de la capacité C de condensateur sachant que I = 0,25 mA.
c) De quoi dépend la capacité C d’un condensateur ?
4/ Calculer la valeur de l'énergie électrostatique emmagasinée par le condensateur à la date t
1
= 48ms.
5/ Calculer la valeur de la constante de temps de ce dipôle RC. On donne : R = 5 KΩ.
Exercice n°2:
1/ Etude de la charge d'un condensateur à travers
un conducteur ohmique de résistance R.
Le générateur de tension possède une f.é.m. E, sa résistance interne
est négligeable ; Le condensateur est initialement déchargé.
a) A la date t = 0s, on relie K à P.
Montrer que l'équation différentielle reliant u
AB
(t) à sa dérivée première s'écrit
sous la forme:
Eu
dt
du
AB
AB
=+τ
en posant τ = RC.
b) Vérifier que
−=
−
τ
t
e1E(t)u
AB
est une solution de l'équation différentielle ci-dessus.
c)* Calculer la constante de temps τ du circuit avec R = 10 kΩ et C = 0,5 µF.
L'interrupteur K est fermé à une date
choisie t = 0 s (origine de temps).
K
C
A
B
La masse
M
Vers
l'ordinateur
u
AB
I
R
M
I
M
R
A
B
K
E
C
P
D

Série n°1 4
èmes
Maths Prof
* Calculer la tension u
AB
aux dates t
d) Tracer l'allure de la courbe représentant u
e) Déterminer la date t
1
, a laquelle la tension
f)
Calculer la valeur de l'énergie emmagasinée dans le condensateur
g) Déterminer l’expression de la tension u
de u
R
(t) en précisant les conditions aux limites.
h)
Préciser sur un schéma, comment doit
l’évolution de la tension u
R
(t)
sur la voie Y
2/ Etude de la décharge d'un condensateur à travers la résistance R.
Le
condensateur étant chargé, on relie K à D à la date t = 0 lue sur un nouveau chronomètre.
a) Etablir la nouvelle équation différentielle reliant u
b)
Sachant que la solution de cette équation est sous la forme
réelle, déterminer l’expression de α
.
c) Donner l'allure de la courbe u
AB
Exercice n°3:
On associe en série un générateur de tension de
f.é.m E avec un
resistor de résistance R et un
condensateur de capacité C = 10 µF.
1/a) Faire un schéma du montage et préciser les
connexions à faire pour visualiser à l'aide d'un
oscilloscope numérique, les tensions
u
R
(t)
respectivement aux bornes du
condensateur et du resistor.
b) Quelle autre grandeur peut-
on étudier à partir
de u
R
(t)? Expliquer.
c) Quelle autre grandeur peut-
on étudier à partir
de u
C
(t)? )? Expliquer.
2/
Le montage, étant réealisé, on obti
l’oscillogramme ci-contre.
Identifier (en le justifiant) les
courbes de cet oscillogramme
3/ Déterminer à partir des oscillogrammes les valeurs de E et de la constante de temps
4/ En déduire la valeur de R.
5/ On donne l'expression de u
C
(t) correspondante
a) Montrer que   .
b
) Déduire l'expression de l'intensité de courant i(t) correspondante.
c
) Déduire la valeur de l'intensité initiale I
d) Déterminer la valeur de I
0
en utilisant l'oscillogramme.
6/ Déterminer l’expression et la
valeur de la charge maximale Q
condensateur.
Exercice n°4:
Pour charger un condensateur, on a réalisé le circuit
L'équation différentielle, donnant la charge q (t) dans un circuit
Maths Prof
: B EN K AHLA J
AWHER
aux dates t
1
= τ , t
2
= 5 τ et lorsque t devient tr
ès grand. On donne E = 100 V.
d) Tracer l'allure de la courbe représentant u
AB
(t).
, a laquelle la tension
 atteint la moitié de E.
Calculer la valeur de l'énergie emmagasinée dans le condensateur
a la date t
g) Déterminer l’expression de la tension u
R
(t) aux bornes de résistor ;
Représenter
(t) en précisant les conditions aux limites.
Préciser sur un schéma, comment doit
-
on brancher un oscilloscope à mémoire pour visualiser
sur la voie Y
1
et la tension de générateur sur la voie Y
2/ Etude de la décharge d'un condensateur à travers la résistance R.
condensateur étant chargé, on relie K à D à la date t = 0 lue sur un nouveau chronomètre.
a) Etablir la nouvelle équation différentielle reliant u
AB
à sa dérivée première.
Sachant que la solution de cette équation est sous la forme
u
AB
(t) = E e
α t
.
AB
(t) dans ce cas.
On associe en série un générateur de tension de
resistor de résistance R et un
condensateur de capacité C = 10 µF.
1/a) Faire un schéma du montage et préciser les
connexions à faire pour visualiser à l'aide d'un
oscilloscope numérique, les tensions
u
C
(t) et
respectivement aux bornes du
on étudier à partir
on étudier à partir
Le montage, étant réealisé, on obti
ent
courbes de cet oscillogramme
.
3/ Déterminer à partir des oscillogrammes les valeurs de E et de la constante de temps
(t) correspondante
: 
 1  
.
) Déduire l'expression de l'intensité de courant i(t) correspondante.
) Déduire la valeur de l'intensité initiale I
0
de courant.
en utilisant l'oscillogramme.
valeur de la charge maximale Q
max
que peut atteindre la charge q(t) de
Pour charger un condensateur, on a réalisé le circuit
schematisé dans la page 3
.
L'équation différentielle, donnant la charge q (t) dans un circuit
fermé constitué d'un générateur
0
u (V)
AWHER
Page 2
ès grand. On donne E = 100 V.
a la date t
2
= 2 ms.
Représenter
l’allure de la courbe
on brancher un oscilloscope à mémoire pour visualiser
et la tension de générateur sur la voie Y
2
.
condensateur étant chargé, on relie K à D à la date t = 0 lue sur un nouveau chronomètre.
à sa dérivée première.
avec α est une constante
3/ Déterminer à partir des oscillogrammes les valeurs de E et de la constante de temps
τ du dipôle RC.
que peut atteindre la charge q(t) de
.
fermé constitué d'un générateur
Courb
e a
Courb
e b
t (s)

Série n°1 4
èmes
Maths Prof : B EN K AHLA J AWHER Page 3
de tension continue de f.é.m. E
et de résistance interne nulle associé en série avec un dipôle RC,
est :
( )
5
1012tq
dt
dq
120
−
=+ .,
: relation ( A ).
(Initialement, à t = 0, le condensateur est non chargé.)
1/ Déterminer l'équation différentielle en q (t) au cours de la charge de condensateur.
2/ Par identification, déduire la valeur de la constante de temps τ de ce dipôle (R,C).
3/ Sachant que E = 12 V, déterminer les valeurs de R et C.
4/a) On admet que la solution de l'équation différentielle est sous la forme  1  
avec A
et α sont des constantes. Déterminer l'expression de q (t). b) Tracer l'allure de la courbe q (t).
c) Déterminer les valeurs de la charge de condensateur aux dates t
1
= 0,12 s et t
2
= 1,2 s. Déduire les
valeurs Ec
1
et Ec
2
de l'énergie potentielle électrique stockée par le condensateur respectivement aux
dates t
1
et t
2
.
d) Déduire de la question 4/a) l'expression de la tension u
C
(t) aux bornes de condensateur.
5/ On décharge le condensateur, et on refait sa charge en remplaçant R par un autre résistor R
1
de
résistance R
1
= 6 kΩ, en gardant le même générateur. Tracer en le justifiant l'allure de la courbe de la
nouvelle charge q
1
(t) (sur le graphique précèdent et avec une autre couleur).
Chimie
ChimieChimie
Chimie :
::
:
Exercice n°1:
Dans un bécher, sont introduits un volume V
1
= 20 mL d’une solution aqueuse de diiode I
2
de
concentration C
1
= 3.10
-2
mol.L
-1
et un volume V
2
= 20 mL d’une solution de thiosulfate de sodium
Na
2
S
2
O
3
( 2 Na
+
+ S
2
O
3 2-
) de concentration C
2
= 4.10
-2
mol.L
-1
.
L’équation chimique qui symbolise la réaction modélisant la transformation chimique qui se produit
dans le bécher est :
I
2
+ 2 S
2
O
3 2 -
S
4
O
6 2 -
+ 2 I
–
1/ Préciser les couples redox mis en jeu au cours de cette transformation.
2/ Dresser le tableau d’avancement de la transformation chimique ayant lieu.
3/ La réaction est totale. Déduire de tableau précédent le réactif limitant de la transformation.
4/ Préciser la couleur de la solution obtenue à l’état final.
Exercice n°2:
On considère la réaction totale et lente : S
2
O
8 2 -
+ 2 I
-
2 SO
4 2 -
+ I
2
On a représenté ci-dessous la courbe de variation de l’avancement x au cours de temps : x = f ( t ).
1/ Comment varie l'avancement x au cours de temps ?
2/ Déterminer graphiquement l'avancement final x
f
.
3/ Déterminer graphiquement le temps de demi réaction
21
t
/
.
4/a) Sachant qu'initialement ( t = 0): n
i I
- = 2.10
- 2
mol, n
i S2O8
2 - = 5.10
- 4
mol n
i I2
= 0 et n
i SO4
2 - = 0;
Dresser un tableau d'avancement de la réaction;
b) Déterminer la composition molaire finale de système ; Quel est le réactif limitant ?
c) Déterminer la composition molaire de système à t = 10 min.
5/ Déterminer en utilisant la figure la valeur de la vitesse moyenne υ
moy
(t
1
,t
2
) de la réaction entre les
dates t
1
= 2 minet t
2
= 9 min et préciser l'unité.
Sens positif
choisi
E
R
C

Série n°1 4
èmes
Maths Prof : B EN K AHLA J AWHER Page 4
6/ Déterminer la valeur de la vitesse initiale υ
0
de la réaction à la date t
0
= 0 min et la valeur de la
vitesse instantanée υ
1
de la réaction à la date t
3
= 6 min.
7/a)Déduire comment évolue la vitesse de la réaction au cours de temps ? Justifier.
b) Préciser le facteur cinétique responsable de cette évolution.
Exercice n°3:
On considère la réaction lente et totale suivante: S
2
O
8 2 -
+ 2 I
-
2 SO
4 2 -
+ I
2
Dans un bécher, on mélange, à l’instant t = 0 s, un volume V
1
= 40 mL d’une solution aqueuse d’iodure
de potassium KI de concentration molaire C
1
= 0,20 mol.L
-1
, avec un volume V
2
= 40 mL d’une solution
aqueuse de peroxodisulfate de potassium K
2
S
2
O
8
de concentration molaire C
2
= 0,05mol.L
-1
. Par une
méthode convenable, on suit la formation du diiode I
2
au cours du temps.
Les résultats expérimentaux ont permis de tracer
la courbe d’évolution de la quantité de matière de
diiode au cours de temps : n
I2
= f (t).
(figure ci-contre)
1/a) Déterminer les quantités initiales des ions I
-
et S
2
O
82-
dans le mélange, notées respectivement n
01
et n
02
.
c) Préciser, en le justifiant, le réactif limitant.
2/ Dresser le tableau d’avancement du système chimique
contenu dans le bécher.
3/ Montrer, à l’aide du graphique, qu’à l’instant t
1
= 30 min, la réaction n’est pas terminée.
a) Donner la composition du système chimique à l’instant t
1
= 30 min.
b) * Déterminer graphiquement la valeur de la vitesse de la réaction à l’instant t = 0 s.
* L’exprimer en mol.s
-1
.
c) Déterminer graphiquement la vitesse volumique de la réaction à l’instant
t
2
= 25 min.
4/ Préciser en le justifiant, si la réaction est terminée ou non, après 55 minutes.
5/ On refait l’expérience mais, en utilisant une solution d’iodure de potassium de concentration
t (min)
n
I2
( 10
-
3
mol)
0
10
50
1
2
t (min)
x ( 10
-
4
mol)
0
2
10
30
1
5

Série n°1 4
èmes
Maths Prof : B EN K AHLA J AWHER Page 5
C
1
’ = 0,40 mol.L
-1
. Préciser en le justifiant, si les grandeurs suivantes sont modifiées ou non par rapport
à l’expérience initiale :
a) L’avancement final de la réaction.
b) La vitesse de la réaction à l’instant t = 0 s.
Exercice n°4:
L'eau oxygénée H
2
O
2
peut oxyder lentement les ions iodures I
-
en milieu acide. On étudie cette
réaction à une température de milieu réactionnel θ
1
.La réaction est totale.
Le conjugué de H
2
O
2
est l'eau H
2
O.
1/ A t = 0, une solution renferme : n
0
( I
-
) = 30 mmol, n
0
(H
2
O
2
) et un excès d'une solution acide.
a) Ecrire l'équation chimique de la réaction qui modélise cette transformation.
b) Citer un catalyseur propre à la réaction entre I
–
et H
2
O
2
.
2/ Une étude expérimentale de la réaction a permis de représenter la courbe ci-dessous.
a) Déduire si la réaction est rapide ou lente ?
b) Déduire de la courbe, lequel parmi les
ions iodures et l’eau oxygéné le réactif limitant ?
3/ a) Dresser un tableau d'avancement de la
réaction étudiée.
b) En exploitant la courbe, déterminer la
valeur de l’avancement final de la réaction.
c) Déterminer la quantité de matière de I
-
restante à la date t
1
= 2 min.
d) Déterminer le temps  de demi-réaction.
4/ Déterminer la vitesse de la réaction à la
date t
2
= 8 min.
5/ Calculer la vitesse moyenne de la réaction
entre l'instant initial t
1
= 0 et l'instant t
2
= 8 min.
6/a)Calculer la vitesse instantanée υ (t
0
= 0) de la réaction à l'instant initial t
0
.
b) Comparer la vitesse υ (t
0
= 0) à celle υ ( t
2
). Interpréter (préciser le facteur cinétique mis en jeu).
7/ On refait l'expérience à une température θ
2
> θ
1
.
Tracer la nouvelle allure de la courbe n (H
2
O
2
) = f(t) (justifier et préciser le facteur cinétique mis en
jeu).
t (min)
n
(H
2
O
2
) ( mmol)
0
6
4
18