Décharge d`un condensateur à travers une résistance R. Texte : les

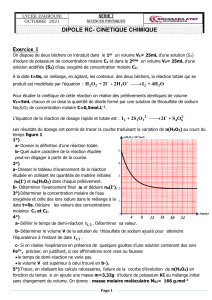
Décharge d'un condensateur à travers une résistance R.
Texte : les courbes ci-dessous représentent l'évolution de la tension u=uc aux bornes du
condensateur et de l'intensité du courant dans le circuit.
Analyse :
Question relative à la valeur de R.
La valeur maximale de l'intensité est égale à : i0 = -U0/R
avec U0 = 6 V et i0 = -1,4 10-3 A d'où R = 6/1,4 10-3 = 4,3 k.
Question relative à la valeur de C.
constante de temps = 0,5 s ( lecture graphe) ; de
plus = RC et R = 4,3 103 .
d'où C= 0,5 /4,3 103 = 1,2 10-4 F.
Charge d'un condensateur.

Texte :
Analyse :
Question relative à la charge initiale du condensateur.
La tension initiale aux bornes du condensateur étant nulle, le condensateur est déchargé et la
charge des armatures vaut :
q = CUAB(t=0) = C*0 = 0 coulomb.
Question relative à la tension uAB(t).
additivité des tensions : uAB + Ri = E avec i = dq/dt et q=CUAB soit i = CduAB/dt
uAB + RCduAB/dt= E
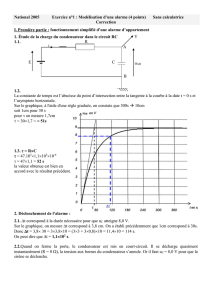
uAB(t) est une fonction exponentielle du temps t de la forme :
uAB(t) = E(1-exp(-t/(RC)).
Lorsque le condensateur est chargé : uAB(t) = E.
Question relative à l'intensité i(t).
uAB(t) =E[1-exp(-t/RC))] et duAB(t)/dt = -E/(RC)exp(-t/RC))
i= CduAB/dt = -E/Rexp(-t/RC).
Valeur maximale de l'intensité |i0|=| -E/R|.
Question relative à la continuité.
La conservation de l'énergie impose la continuité de la tension aux bornes du condensateur et
discontinuité de l'intensité.