Vibrations des arbre..

____________________________________________________
_______________________________________________
ICAM2 – Nantes / Génie-Mécanique
T.P. Comportement Dynamique (J. Besnier, R. Tarbadar) 1/8
TP5. VIBRATIONS
des arbres rotatifs
MONTAGE
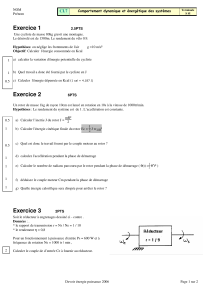
L'arbre est guidé en rotation par deux paliers rotulants.
Vue de dessus
15 Mils = 0.4 mm ( ≈ 3 Volt )

____________________________________________________
_______________________________________________
ICAM2 – Nantes / Génie-Mécanique
T.P. Comportement Dynamique (J. Besnier, R. Tarbadar) 2/8
I) Introduction :
Une des causes les plus fréquentes de vibration est certainement la force tournante
(centrifuge) due au fait qu’il n’est généralement pas possible de faire coïncider l’axe de
rotation avec le centre de gravité du rotor. Il en résulte que l’arbre est soumis à un
champ de force qui le déforme. Ces déformations à leur tour déplacent les centres de
gravité, donc augmentent les forces.
Les équations de la mécanique permettent de déterminer les déformations de l’arbre si
l’on connaît les efforts appliqués et les caractéristiques mécaniques du rotor et des
appuis. A l’inverse, connaissant les déformations, on peut en déduire les efforts, et par
conséquent savoir comment les compenser (équilibrage des arbres).
Le principe de base de l’équilibrage consiste en théorie à faire coïncider l’axe de rotation
avec la ligne des centres de gravité. En pratique, on se contente de placer des masses
correctrices dans des plans d’équilibrages accessibles. On n’équilibre pas, mais on crée un
autre déséquilibre !!!
Le rotor dans sa vibration constitue un système vibrant continu et admet une infinité
ordonnée de modes propres. Chacune correspond à une pulsation propre ω
p
associée à une
forme du rang p . En fait, on n’en observe généralement qu’un petite nombre, car les
formes propres qui correspondent à des fréquences élevées sont assez amorties pour que
les modes correspondants n’existent réellement pas (amortissement plus que critique).
L’objectif de ce TP :
• Se familiariser avec le calcul des deux fréquences propres fondamentales par les
méthodes d’énergie simplifiées « la méthode de RAYLEIGH »
• Analyser le comportement vibratoire d’un arbre tournant.
• Apprendre à déterminer la position du balourd par des simples mesures de
déplacement.
II) Caractéristiques du rotor
1) Aspects théoriques
Nous allons étudier le cas simple d’un rotor constitué d’un arbre flexible et d’un disque
rigide dont le centre de masse et le centre géométrique ne coïncident pas, ce qui peut
être modélisé par deux masses : M masse centrée et m la masse excentrée qu’on va
appeler la masse du balourd (m <<< M). L’arbre est porté par deux paliers rotulants.
- M masse du rotor ,
- m masse du balourd ,
- R rayon du balourd ,
- φ
φφ
φ position angulaire du balourd ,
- Ω
ΩΩ
Ω vitesse angulaire du rotor ,

____________________________________________________
_______________________________________________
ICAM2 – Nantes / Génie-Mécanique
T.P. Comportement Dynamique (J. Besnier, R. Tarbadar) 3/8
L’équation générale du mouvement
En analysant les forces agissantes sur la masse M, on distingue quatre types de forces :
les forces d’inertie,
les forces de raideur,
les forces d’amortissement interne ou externe
les forces d’excitation (force centrifuge)
L’objectif de cette analyse est de déterminer le
déphasage Ф entre la force d’excitation et le déplacement
accessible à la mesure. On commence par la
détermination des relations de phase entre les trois
forces : raideur, inertie et amortissement
R APPEL DES RELATIONS ENTRE LES GRANDEURS D ’ UN MOUVEMENT
VIBRATOIRE EN REGIME PERMANENT HARMONIQUE :
déplacement : d(t) = d cos(Ω t)
vitesse : v(t) = Ω d cos(Ω t + Л/2)
accélération : a(t) = Ω² d cos(Ω t +Л)
On en déduit les relations d’amplitudes et de phases suivantes :
1) Les relations d’amplitudes : a = Ω² d et v = Ω d
2) La vitesse et l'accélération sont respectivement en quadrature et en opposition de
phase avec les déplacements
En factorisant le terme de déplacement, il
apparaît la raideur dynamique Z = F/d
On note que :
2
.
tan
.
d
K M
φ
Ω
=−Ω

____________________________________________________
_______________________________________________
ICAM2 – Nantes / Génie-Mécanique
T.P. Comportement Dynamique (J. Besnier, R. Tarbadar) 4/8
à basses vitesses:
Pour des valeurs de
Ω
faibles, le terme de
K
F
d
0
= , 0
≈
Φ
la raideur est dominant, les
deux forces d’amortissement et d’inertie restent négligeables.
L’équation se réduit à : )(. tFdk
=
et,
0
Φ ≈
La raideur dynamique est quasiment en phase avec la raideur statique.
à la résonance, Ω = ω
n
= √(K/M), le terme dominant est le terme d’amortissement car
les termes d’inertie et de rappel élastique se compensent, l’équation (1) se réduit à :
)(. tfvD
=
,
ω
D
F
d
0
= et φ = -90°
Nous observons aussi au voisinage de ω
n
une variation rapide de phase et d’amplitude
(voir fig. et vitesse critiques)
Pour Ω >> ω
n,
le terme dominant de l’équation (1) est le terme d’inertie et l’équation se
réduit à : )(. tFaM
=
,
ω M
F
d
0
≈ et
π
Φ ≈ −
, la déformation est opposée à la force
(m tente d’être immobile)
III) VITESSES CRITIQUES, PULSATIONS PROPRES
La vitesse critique
c
ω
est celle qui correspond à un maximum de l’amplitude de
vibrations de flexion. C’est donc pour cette vitesse que les contraintes supportées par
le rotor seront maximales. La détermination théorique de cette vitesse n’est pas
évidente car il nécessite notre connaissance de l’amortissement.
D’autre part, l’analyse précédente a mis en évidence un autre critère concernant la
phase de la vibration par rapport à l’effort. Sa variation est rapide autour de la
pulsation propre ω
n.
Le déphasage est égal à 90° lorsque Ω = ω
n

____________________________________________________
_______________________________________________
ICAM2 – Nantes / Génie-Mécanique
T.P. Comportement Dynamique (J. Besnier, R. Tarbadar) 5/8
Les deux pulsations étant très voisines dans le cas des rotors réels, peu dissipatifs, on
pourra les confondre et utiliser les deux critères précités pour détecter la vitesse
critique mesurée. C’est pour cette raison que l’analyse théorique utilisée pour la
détermination des vitesses critiques traite un système conservatif.
1) Calcul (Méthode de RAYLEIGH)
La méthode de Rayleigh est l’une des méthodes approchées permettant le calcul des
premières pulsations propres d’un système continu. La base théorique de cette
méthode fait l’objet du T.P. « vibration des poutres continues en flexion », où nous
avons obtenu l’expression de la pulsation propre :
Application numérique :
1-Principe de discrétisation :
Un rotor continu, aussi compliqué soit-il, peut toujours être discrétisé en un
nombre fini de nœuds délimitant des éléments droits, représentant des tronçons du
rotor.
Si l’on suppose que les propriétés massiques des éléments sont concentrées aux
nœuds (centre de gravité de chaque tronçon), et que leurs propriétés élastiques
apparaissent comme des raideurs tenant compte des degrés de libertés (déformation) ;
un rotor continu peut être transformé en un système couplé de masses, d’amortissements
et de raideurs.
Avec la discrétisation du rotor en 5 tronçons (i) de longueur l
i
:
L
1
= L
5
= 110 mm ; L
3
= 220 mm ; L
2
= L
4
= 25 mm ; diamètre de l’arbre =10 mm,
ρ = 7,8 Kg/dm
3
; E = 190 000 Mpa, masse de chaque disque = 800 g.
∫
∫
=⇒
l
l
dxxSu
dxxEIu
0
0
)²(
)"²(
²
ρ
ω