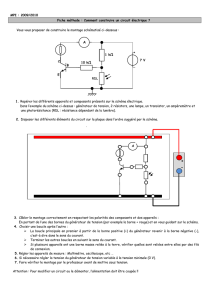
Construction de R par les quasi-morphismes de Z

Construction de Rpar les quasi-morphismes de Z
Salim Rostam
Journées 4a de l’ENS Rennes
23 janvier 2015

Sommaire
1Anneaux des classes de quasi-morphismes
2Structure de corps commutatif ordonné vérifiant la propriété de
la borne inférieure

1Anneaux des classes de quasi-morphismes
Quasi-morphismes
Deux lois de composition
2Structure de corps commutatif ordonné vérifiant la propriété de
la borne inférieure
Structure de corps commutatif
Ordre garantissant la propriété de la borne inférieure

1Anneaux des classes de quasi-morphismes
Quasi-morphismes
Deux lois de composition
2Structure de corps commutatif ordonné vérifiant la propriété de
la borne inférieure
Structure de corps commutatif
Ordre garantissant la propriété de la borne inférieure

Quasi-morphismes
Définition
Pour k∈N, une fonction f:Z→Zest un élément de QHksi :
∀m,n∈Z,|f(m+n)−f(m)−f(n)| ≤ k
♣
Exemples
QH0=Hom(Z,Z)
Pour α∈Qon a n7→ E(αn)∈QH2
Définition (Quasi-morphismes)
L’ensemble des quasi-morphismes de Zest QH := ∪k∈NQHk
♣