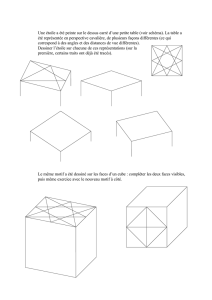
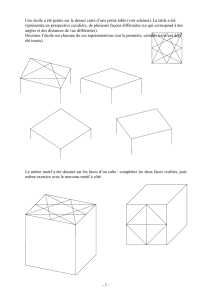
Axiome du cube et foncteurs de Quillen.

ANNALES DE L’INSTITUT FOURIER
JEAN-PIERRE DOERAENE
DANIELTANRÉ
AxiomeducubeetfoncteursdeQuillen.
Annales de l’institut Fourier, tome 45, no4 (1995), p. 1061-1077.
<http://www.numdam.org/item?id=AIF_1995__45_4_1061_0>
© Annales de l’institut Fourier, 1995, tous droits réservés.
L’accès aux archives de la revue « Annales de l’institut Fourier »
(http://annalif.ujf-grenoble.fr/), implique l’accord avec les conditions
générales d’utilisation (http://www.numdam.org/legal.php). Toute
utilisation commerciale ou impression systématique est constitu-
tive d’une infraction pénale. Toute copie ou impression de ce fi-
chier doit contenir la présente mention de copyright.
Article numérisé dans le cadre du programme
Numérisation de documents anciens mathématiques
http://www.numdam.org/
1

Ann. Inst. Fourier, Grenoble
45, 4 (1995), 1061-1077
AXIOME DU CUBE ET FONCTEURS DE QUILLEN
par J.-P. DOERAENE et D. TANRÉ
La LS-catégorie a été définie par Lusternik et Schnirelmann en 1934
dans [7] pour minorer le nombre de points critiques d'une variété compacte
sans bord. Plusieurs caractérisations équivalentes montrent qu'il s'agit d'un
invariant du type d'homotopie; leur extension au cadre des catégories à
modèles fermées, M, fait l'objet de [3] et [5].
Dans [3], le premier auteur a montré que les présentations de
Whitehead et Ganea sont équivalentes lorsqu'un axiome supplémentaire
est requis : l'axiome du cube. La philosophie de ce dernier axiome est
que les sommes amalgamées homotopiques sont préservées par les produits
fibres homotopiques.
Le cadre choisi dans [3] pour cette démonstration présente deux
restrictions importantes :
• L'axiome du cube est un axiome global sur toute la catégorie. Or il
peut exister des catégories à modèles ne vérifiant pas l'axiome du cube et
dans lesquelles les définitions de Whitehead et Ganea coïncident pour une
certaine classe d'objets. Seule une caractérisation au niveau des morphismes
de la catégorie peut permettre d'appréhender cette situation.
• Un axiome supplémentaire, la propreté, est requis pour M. alors
que plusieurs catégories à modèles fermées ne le vérifient pas, par exemple,
la catégorie des ensembles simpliciaux r-réduits, (<?r).
Dans ce travail, nous nous affranchissons de ces deux restrictions,
en définissant d'abord les produits fibres homotopiques dans le cas d'une
catégorie à modèles sans axiome de propreté. Nous introduisons ensuite
les familles «de flèches du cube» qui permettent d'obtenir l'équivalence
Mots-clés : Catégorie de Lusternik-Schnirelmann - Catégorie homotopique - Axiome
du cube.
Classification math. : 55M30 - 55U35.

1062 J.-P. DOERAENE ET D. TANRÉ
entre les définitions de Whitehead et Ganea. Enfin, nous montrons que les
fondeurs de Quillen « conservent » les flèches du cube.
En particulier, bien que la catégorie Sr ne vérifie pas l'axiome du cube
et ne soit pas propre, notre approche permet de montrer que l'équivalence
des définitions de Whitehead et Ganea pour une classe d'ensembles
simpliciaux de Sr s'étend à une sous-catégorie de la catégorie des algèbres
de Lie différentielles (r — l)-réduites. Cet exemple de la catégorie Sr est
développé en appendice aux deux premiers paragraphes.
1. Produit fibre homotopique.
Cette section est une présentation des principaux objets ; elle contient
notamment la définition et les principales propriétés des produits fibres
homotopiques. Les démonstrations sont regroupées à la fin du paragraphe.
En appendice, un exemple de produit fibre homotopique dans la catégorie
des ensembles simpliciaux r- réduits est développé.
Rappelons qu'une catégorie à modèles fermée est une catégorie M.
munie de trois classes de flèches, appelées respectivement fibrations (fib, +^),
cofibrations (cof, +->), équivalences faibles (we, -^), vérifiant les axiomes
suivants :
(CMi) : M, est fermée pour les limites inductives et projectives finies.
(CMs) : Si le composé gf est défini dans M. et si deux quelconques de /, g,
gf sont des équivalences faibles, le troisième l'est également.
(CMs) : Un rétracte d'une fibration, (resp. d'une cofibration, resp. d'une
équivalence faible), est une fibration, (resp. cofibration, resp. équi-
valence faible).
(CM4) : Tout diagramme commutatif en trait plein
A ———. X
+ ^ i
B———> Y
peut être complété en un diagramme commutatif par une flèche en
pointillé si l'une des conditions suivantes est satisfaite :
a) i est une cofibration et une équivalence faible, p est une
fibration ;

AXIOME DU CUBE ET FONCTEURS DE QUILLEN 1063
b) i est une cofibration, p est une fibration et une équivalence
faible.
(CMs) : Toute flèche / peut se factoriser de deux façons :
a) / = jn, où i est une cofibration et une équivalence faible, p
est une fibration ;
b) / = çj, où j est une cofibration, q est une fibration et une
équivalence faible.
Dans la catégorie A4 , deux objets A et B sont faiblement équivalents
s'ils sont reliés par une suite finie d'équivalences faibles.
Rappelons également qu'un objet A est fibrant si l'application A—^e
est une fibration, où e est un élément final dans M.. Remarquons que toute
fibration de but un objet fibrant a un objet fibrant en source. L'axiome
(CM5) a) implique que tout objet A admet un modèle fibrant £', A ^ E.
Considérons la catégorie M.2 des flèches de M. ; ses objets sont les
flèches de M. et ses morphismes sont les carrés commutatifs
A-^B
^ représentés par (a; / | g\ b).
4-
X-^Y
Notons b [ g le produit fibre de b et g ainsi que (a, /) : A —> b [ g la
flèche obtenue par propriété universelle.
Remarque 1. — À partir des axiomes précédents de catégorie à
modèles fermée, il est facile de montrer (voir [l], [9]) que, si le carré
b[f —f— B
"i l6
4- „ 4,
X ——^ Y
est un produit fibre dans lequel b est une fibration (resp. fibration et
équivalence faible), alors h' est une fibration (resp. fibration et équivalence
faible).
On munit M2 d'une structure de catégorie à modèles fermée, (voir [l],
II, 1.5.), en choisissant :

1064 J.-P. DOERAENE ET D. TANRÉ
• pour équivalences faibles les flèches (a; / | g', b) telles que / et g sont
des équivalences faibles ;
• pour fibrations les flèches (a; / | g\ b) telles que /, g et (a, /) sont des
fibrations.
Remarque 2.
• La catégorie des cubes, Al3, peut être considérée comme la catégorie
des flèches de A42 .
• Un objet fibrant dans A42, (resp. AI3), est une fibration entre
objets fibrants de M. , (resp. A42). Par conséquent, tout carré commutatif
(c'est-à-dire un objet de A43) admet un modèle constitué de fibrations entre
objets fibrants.
• Deux flèches de A4 sont dites faiblement équivalentes si elles le sont
comme objets de Al2.
DÉFINITION 1. — Un carré dans A4 est appelé fibrant-fibre, s^il est un
produit fibre constitué de fibrations entre objets fibrants, c'est-à-dire s'il
est à la fois un produit fibre dans Al. et un objet fibrant dans Al2.
DÉFINITION 2. — Un carré dans A4 est appelé produit fibre
homotopique (pfh) si, comme objet de A43, il est faiblement équivalent
à un carré fibrant-fibré.
PROPOSITION 1. — Soit (/,/') un couple de flèches de A4 de même
but. Considérons des décompositions f = pi = pï et f = p' i1 = p' î de f
et /', dans lesquelles p,p,p1,p1 sont des fibrations, î, î, i', V des équivalences
faibles. Alors les produits fibres p [ p' et p [ p' sont faiblements équivalents.
DÉFINITION 3. — Avec les hypothèses de la proposition 1, le produit
fibre p [ p' est un produit fibre homotopique de f et f. Par abus de
notation, il sera désigné par / U /'.
Cette notion est un invariant du type d'homotopie, comme le montre :
PROPOSITION 2. — Considérons deux couples de flèches de A4, de
même but, faiblement équivalents, (/, /') et (/, /'). Alors les produits fibres
homotopiques f [h f et f [h f sont faiblement équivalents.
Les objets définis ci-dessus sont reliés par :