Les effets d`une force sur un solide dépendent, non seulement de

STI2D \ ET \ -Forces & Moments- 1
Les effets d’une force sur un solide dépendent, non seulement de son intensité et de
sa direction, mais aussi du moment quelle peut engendrer. Le moment d’une force mesure
l’effet à causer une rotation aux objets sur lesquels elle agit.
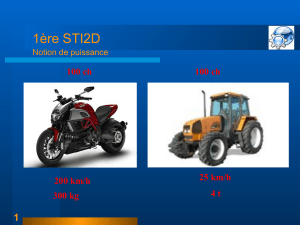
Exemple :
Moment scalaire d’une force par rapport à un point
1-Définition :
Le moment d’une force £F par rapport au point A, noté MA(£F ),
est égal au produit de F par le bras de levier d :
MA(£F ) : est exprimé en Nm
F : est exprimé en N
d : est exprimé en m (distance entre A et £F)
Par convention :
Si £F fait tourner le solide autour de A dans le
sens trigonométrique, le moment est ……………..
Si £F fait tourner le solide autour de A dans le
sens des aiguilles d’une montre, le moment est
…………………………………
Exemple 1 :
Déterminer MA(£F ) sachant que :
 F= 300 N
 AB= 0,5m
 α = 40°
Il faut calculer la distance d :
MA(£F ) =

STI2D \ ET \ -Forces & Moments- 2
Exemple 2 :
Déterminer la valeur de || £F 2 || lorsque le solide So
est à l’équilibre : MA(£F 1) + MA(£F 2)= 0
MA(£F 1) =
MA(£F 2)=
Exercice 3:
Pour serrer un écrou, on utilise une clé à
molette. Pour évaluer l’effort de serrage
calculez le moment £B 3/2 par rapport au
centre A de l’écrou dans les cas suivants :
MA(££B 3/2) =
α = 0°
MA(££B 3/2)=
α = 30°
MA(££B 3/2)=
α = 45°
MA(££B 3/2)=
α = 60°
MA(££B 3/2)=
α = 90°
MA(££B 3/2)=
Conclusion :
…………………………………………………………………………………………………………………………………………..

STI2D \ ET \ -Forces & Moments- 3
2-Théorème de Varignon
Le moment de la force £F par rapport au point A est égale à la somme des moments de
ses composantes £U et £V par rapport au même point .
MA(£F )= F.d
MA(£U )= - U. dU
MA(£V )= V. dV
MA(£F )= V. dV - U. dU
Exercice 4 :
Déterminer MA(£F ) de la force £F .
Fx =
Fy =
MA(£F ) = MA(£U )+ MA(£V)

STI2D \ ET \ -Forces & Moments- 4
Vecteur -moment
Dans l’espace le moment d’une force doit être décrit sous forme vectorielle.
1- Définition :
O
x
y
z
()
A
B
)F(
A
M
£F
Le moment d’un vecteur £F d’origine A, par
rapport à un point de l’espace B, est le
vecteur défini par la relation :
F ^ AB)F(
AM
Ce moment est un vecteur lié dont les caractéristiques sont :
- Son origine : le point A
- Sa direction : la droite perpendiculaire au plan formé par _AB et £F
- Son sens : tel que le trièdre (_AB , £F ,
)F(
A
M
soit direct
- Son intensité :
)F,ABsin( . F . ABF)(
AM
Attention : Les caractéristiques du vecteur
)F(
A
M
dépendent de la position du point A.

STI2D \ ET \ -Forces & Moments- 5
2- Vecteur – moment en coordonnées cartésiennes :
Déterminer le moment en A de la force £F
_AB = 0.5 x + 0.3 y + 0 z
£F = Fx x + Fy y + Fz z
Fx = ………………………………
Fy = ………………………………
Fz = ………………………………
F ^ AB)F(
AM
…………………………………………………..
_AB ^ £F …………………………………………………..
…………………………………………………..
)F(
A
M
…………..x + ………….. y +……….z
Couple et vecteur-couple
1- Définition :
2- Signe du couple
Couple positif
Couple négatif
Le moment engendré par forces égales et opposées ayant des
lignes d’action différentes ( non colinéaires) constitue un
couple ( M)
M=