autre cours au format PDF

LYSZYK HACHEUR SERIE
Étude du Hacheur série
La version 1 considère que tout est idéal .
Cette version suppose que le courant de charge n'est plus constant mais contient une ondulation de type
linéaire non négligeable .
I) Généralités
1) Introduction
C’est un interrupteur électronique qui hache une tension continue en portion plus ou moins large .
ce qui permet d’obtenir une tension de forme créneau et de valeur moyenne réglable à partir d’une
tension fixe et ceci, avec un rendement voisin de 1.
Il joue le même rôle en continu que le transformateur en alternatif.
Il commande le débit d’un générateur de tension dans un générateur de courant.
On dit aussi que c’est un hacheur à liaison direct car il n’y a pas d’élément de stockage de l’énergie
entre son entrée et sa sortie .
Son symbole
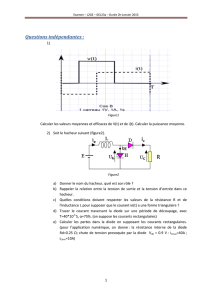
2) Schéma de principe
Le hacheur est formé d’un interrupteur électronique K commandée et d’une diode .
U
K
D
ic
K fermé
D bloquée
U
ic
uc
h
K ouvert
D conduit
U
ic
uc

LYSZYK HACHEUR SERIE
II) Étude du fonctionnement sur charge R,L
1) Montage
U
K
D
RL
R
L
U
ch
i
H
i
ch
i
D
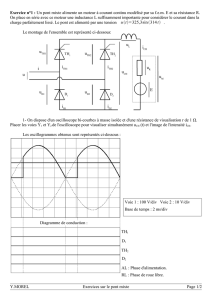
2) Formes d’ondes :(Voir courbes de TP )
3) Équations générales et résolution.
a) Équations de fonctionnement
Quelque soit l’instant , nous pouvons écrire la maille :
ucht= R∗ichLdich
dt
équation (1)
Il suffit ensuite de remplacer uch par sa valeur suivant l’instant considéré .
0 < t < T
T < t < T
U
K
Est fermé
R
L
U
ch
i
H
i
ch
D
RL
R
L
i
ch
i
D
Uch=0
La diode de roue libre conduit
d’où uch = 0 , ce qui donne pour l’équation (1)
0=R∗ich+Ldich
dt
La diode de roue libre est bloquée
la tension uch est égale à U , ce qui donne pour
l’équation (1)
U=R∗ichLdich
dt
(3)
(2)

LYSZYK HACHEUR SERIE
b) Valeur moyenne de la tension uc
Ucmoy =R∗Ichmoy +[ Ldich
dt ]
moy
=R∗Ichmoy
ceci du coté droit de uc(t)
Ucmoy=α U
du coté gauche de la diode de uc(t)
on fait l'égalité entre les deux expressions
Ucmoy =α U=R∗Icmoy
c) Expressions de i(t)
On considère les deux cas précédents , ce qui nous amène à donner deux expressions de ich(t).
0 < t < T
Si on suppose que la constante de temps
= L
R
est très grande devant la
période ( rapport de 10 )
T
≪1
alors l'équation
U=R∗ich+Ldich
dt
(2)
donne comme solution une droite . Le courant est minimal à l'instant où l'interrupteur K se ferme
( voir les courbes expérimentales )
On voit à partir de la courbe que la
valeur moyenne du courant sera
donnée par
Ichmoyen=Imax+Imin
2
dans le cas où le rapport
T
n'est pas très inférieur à 1 on a une forme exponentielle qui
apparaît dans le cas contraire
i1t= U
R Imin−U R1−t
i1t= U
R
t
Imin1−t
(4) .
i1t=Imint
U
R−Imin
T < t < T
uch=R∗ich Ldich
dt
(2) devient
0=R∗ichLdich
dt
K se ferme
K se ferme
Ich est minimal
Ich
t
Ichmin
Ichmax
K s'ouvre
0T2T
Ichmax
0=R∗ich Ldich
dt
0=R∗ich Ldich
dt
0=R∗ich Ldich
dt

LYSZYK HACHEUR SERIE
La résistance R ne peut pas être négligée mais on peut avoir le rapport
L
R≪T
l'équation
0=R∗ichLdich
dt
nous donne
L
R
t
Maxtr
eIiti
*
12
*)(
(5) elle peut être remplacée par celle d'une
droite partant de Icmax et de pente R/L
ich2=Ichmax 1−T
avec
= L
R
ich2=Ichmax 1−R
LT
d) Calcul de  ich
En utilisant les expressions de ich1 et ich2 précédentes nous pouvons en tirer une relation entre Imax
et Imin . Nous obtenons
ax
T
I
R
U
R
U
Ti Im)1(*)(
min1
in
T
IiTi
Maxtr
Im)
)1(
1(*)1(
12
T
R
U
III
Max
1
min
Comme = L/R en remplaçant dans l’expression précédente nous obtenons
T
L
U
III
Max
1
min
On constate que l'ondulation dépend de l'inductance L mais aussi de la période de hachage .
b) Étude du  i en fonction de 
L’étude se fera à partir de la dérivée . Nous obtenons le maximum pour  = 0,5
Ich max=Ichmax−Ichmin=T∗U
4∗L
III) Étude sur charge R,L,E ( cas où R est suffisamment faible pour linéariser les équations )
1) Formes d’onde et équations
➢Dans le cas du fonctionnement en conduction continue les formes d’onde sont les mêmes que pour
la charge RL .
0 < t < T
La diode de roue libre est bloquée la tension uch est égale à U , ce qui donne pour l’équation (1)
U=E+R ich +Ldich
dt
(11)
T < t < T
La diode de roue libre conduit d’où uch = 0 , ce qui donne pour l’équation (1)
0=E+Rich+Ldich
dt
Le hacheur est alimenté sous U .
La valeur moyenne de uc est donnée par <uch> = Ucmoy
Ucmoy=α U

LYSZYK HACHEUR SERIE
mais c'est aussi Ucmoy = E + R <ich> +0
car la valeur moyenne de la tension aux bornes d'une inductance pure est nulle .
On en déduit que :
Ucmoy=αU=E+R Ichmoy
➢Si le courant de charge s'annule lorsque k est ouvert alors nous verrons apparaître un
palier de valeur égale à la tension E .
2) Équations de fonctionnement
Quelque soit l’instant , nous pouvons écrire la maille :
ucht= ER∗ichLdich
dt
équation (10)
Il suffit ensuite de remplacer uch par sa valeur suivant l’instant considéré .
0 < t < T
La diode de roue libre est bloquée la tension uch est égale à U , ce qui donne pour l’équation (1)
U = E + R ich + L dich/dt (11)
T < t < T
La diode de roue libre conduit d’où uch = 0 , ce qui donne pour l’équation (1)
0 = E + R ich + L dich/dt (12)
T< t < T
L’intensité de ich est nulle , la diode de roue libre est bloquée et l’interrupteur K est ouvert, nous avons
uch = E (13)
3) Valeur moyenne de uch(t)
Utilisons l’équation générale de la maille et prenons la valeur moyenne .
uch ( t ) = E + R ich + L dich/dt équation (10)
< uch ( t )> = E + <R ich> + <L dich/dt> la valeur moyenne de la tension aux bornes d’une inductance est
nulle .
Ich conduction discontinue
0aTbTT
Ichmax
U
E
0aTbTT
U
EE
U
uch
t
t