exercices sur la mcc

Tset2 07/08
1 /
I) Problème 1
Pour un moteur à excitation indépendante, parfaitement compensé, on dispose des caractéristiques suivantes :
résistance de l'induit : R= 1 Ω
tension nominale aux bornes de l'induit : Un = 220 V
intensité nominale du courant dans l'induit : In = 20 A
fréquence de rotation nominal : nn = 1500 tr/min
intensité nominale du courant d'excitation : in = 1.5 A
Dans tout le problème, on supposera que les pertes dans le fer et les pertes mécaniques sont négligeables.
ce moteur entraîne une machine dont le couple résistant Cr varie en fonction de la fréquence de rotation n. La
caractéristique Cr = f(n) peut être assimilée à une droite passant par les points n = 0 Cr = 12 N.m et n =
2000tr/min Cr = 30 N.m .
L'intensité du courant d'excitation est maintenue constante et égale à 1.5 A
I.1) Calculer le rapport K = E'/n de la f.c.é.m du moteur à fréquence de rotation n (en tr/min)
I.2) Donner la relation entre le moment du couple moteur C et l'intensité i du courant
I.3) Après avoir exprimé l'intensité I en fonction de la tension U aux bornes de l'induit et de E', montrer que
la caractéristique mécanique du couple a pour expression : C = (4/π).(U -K.n ) avec C : moment du couple
électromagnétique . Calculer les points de fonctionnements correspondants à U = Un et U = 200 V puis la
tension d'alimentation minimum de démarrage.
II) Problème 2
Un moteur à courant continu , dont la réaction magnétique d'induit est parfaitement compensée, est utilisé à
la traction d'un véhicule.
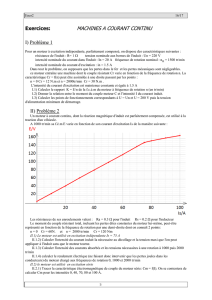
A 1000 tr/min sa f.é.m E varie en fonction de son courant d'excitation Is de la manière suivante :
Is (A) 0 10 20 30 40 50 60 70 75 80 90 100
E (V) 5 24 43 63 82 101 120 140 150 154 161 167
Les résistances de ses enroulements valent :
Ra = 0.3 Ω pour l'induit
Rs = 0.2 Ω pour l'inducteur
Le moment du couple résistant total, incluant les pertes dites constantes du moteur lui-même, peut-être
représenté en fonction de la fréquence de rotation par une demi-droite dont on connaît 2 points:
n = 0 Cr = 60N. et n = 2000 tr/min Cr = 120 Nm
II.1) Le moteur est utilisé en excitation indépendant Is = 75 A
II.1.1) Justifier le choix du courant d'excitation IS
II.1.2) Calculer l'intensité du courant induit Ia nécessaire au décollage et al tension maxi que l'on peut
appliquer à l'induit sans que le moteur tourne.
II.1.3) Calculer l'intensité des courants absorbés et les tensions nécessaires à une rotation à 1000 puis 2000
tr/min
II.1.4) calculer le rendement électrique (ne faisant donc intervenir que les pertes joules dans les
conducteurs) du moteur chargé aux fréquences de rotation 0, 1000 et 2000 tr/min
II.2) le moteur est utilisé en excitation série
II.2.1) Tracer la caractéristique électromagnétique de couple du moteur série: Cm = f(I). On se contentera de
calculer Cm pour les intensités 0, 40, 70, 80 et 100 A.
II.2.2) En déduire l'intensité des courants absorbés au décollage, puis aux fréquences de rotation 1000 et
2000 tr/min
II.2.3) calculer les tensions à appliquer au moteur pour obtenir ces 3 fonctionnements

Tset2 07/08
2 /
II.2.4) calculer le rendement électrique (défini comme dans la question précédente) lors de ces 3
fonctionnements.
III) Problème 3
On considère un moteur série bipolaire dont les caractéristiques sont les suivantes :
Nombre de conducteurs actifs : 500 ( avec 2 voies d'enroulements)
Résistance de l'induit : Ra = 0.8 Ω
Résistance de l'inducteur : Rs = 1.2 Ω
Courant nominal : 15 A
Tension d'alimentation nominale : 480 V
Dans tout le problème, on négligera les pertes autres que par effet Joule.
On admet que le flux est proportionnel à l'intensité du courant si celle-ci ne dépasse pas 15 A et que, pour des
intensités supérieures à cette valeur , le flux reste constant égal à 60 mWb.
III.1) Donner l'équation du flux en fonction de l'intensité si I < 15 A
III.2) Le moteur fonctionne à son point nominal. Déterminer les valeurs de la f.c.é.m, de la fréquence de
rotation, de la puissance utile et du couple utile.
III.3) Déterminer les mêmes valeurs pour I = 20A puis pour I = 10A
III.4) Déterminer le courant absorbé si le couple fourni devient :
+ la moitié du couple nominal
+ les 5/4 du couple nominal
IV) problème IV L’énergie d’un treuil est fournie par un moteur à courant continu à excitation
indépendante dont l’induit et l’inducteur sont alimentés sous une tension U = 230 V.
En charge, le treuil soulevant verticalement une charge à la vitesse de 4 m/s, le moteur tourne à une vitesse de
1200 tr/min et son induit absorbe une puissance électrique de 17,25 kW. La résistance de l’induit est de 0,1
Ω
;
celle de l’inducteur de 46
Ω
; les pertes dites constantes ont pour valeur 1 kW; l’accélération de la pesanteur sera
prise égale à g = 10 m/
s
2; le rendement du treuil est de 0,75.
Calculer:
a. les courants absorbés par l’induit et l’inducteur;
b. la force électromotrice du moteur;
c. la puissance utile du moteur;
d. le couple utile du moteur;
e. le rendement du moteur;
f. le rendement global de l’équipement;
g. la masse soulevée par le treuil.
V) Un moteur shunt est alimenté sous une tension constante de 200 V.
Il absorbe un courant I = 22 A. La résistance de l’inducteur est R = 100
Ω
, celle de l’induit
R
a
=
0
5
,
Ω
. Les
pertes constantes sont de 200 W.
V.1. Calculer:
a. les courants d’excitation et d’induit;
b. la force contre-électromotrice;
c. les pertes par effet Joule dans l’inducteur et dans l’induit;
d. la puissance absorbée, la puissance utile et le rendement global.
V.2. On veut limiter à 30 A l’intensité dans l’induit au démarrage. Quelle doit être la valeur de la résistance du
rhéostat de démarrage?
V.3. On équipe le moteur d’un rhéostat de champ. Indiquer son rôle. Dans quelle position doit se trouver le
rhéostat de champ au démarrage? Justifier votre réponse.
VI) On considère un moteur à courant continu, son excitation possède une valeur telle qu’à
350 tr/min la force électromotrice est égale à 250V. La résistance totale de l’induit est 0,005
Ω
et le courant
maximum admissible est 2000 A.
On met brusquement ce moteur sous tension à l’aide d’un réseau dont la tension est 250 V.

Tset2 07/08
3 /
Le démarrage se produit sans couple résistant sur l’arbre et l’on néglige les frottements. Le moment d’inertie est
J = 230 kg.
m
2.
VI.1. Quel rhéostat de démarrage faut-il prévoir pour que le courant ne dépasse pas la valeur admissible ?
VI.2. Ce rhéostat étant en place, quelle est la loi de variation en fonction du temps de la vitesse de rotation N?
Au bout de combien de temps le moteur aura-t-il atteint à 5% près sa vitesse à vide?
VI.3. Au bout de combien de temps le courant est-il réduit à 1000 A?
VII) Extrait de la SESSION DE 1995
Le moteur étudié est un moteur à aimant permanent. Son rotor est constitué d’un disque isolant sur
lequel sont collés des conducteurs en lamelles. L’induit ne comportant pas de fer, les pertes
ferromagnétiques sont négligeables.
Caractéristiques du moteur :
Résistance d’induit : R = 1,5 Ω ; inductance d’induit négligeable ;
Moment d’inertie : J = 2,35 10-4 kg.m2
Valeurs nominales :
Tension : U = 65 V
Courant absorbé : I = 8 A
Vitesse : 3000 tr/mn
1. ETUDE DU MOTEUR
Le moteur étudié doit vaincre dans tous les cas un couple de frottement mécanique dont le moment est donné par
la relation :
Tp = Tf + KdΩ où Tf = 2,6 10-2 N.m
et Kd = 1,43 10-4 N.m/rad.s-1
Ω représente la vitesse angulaire du rotor exprimée en radians par seconde.
1.1.Pour le fonctionnement nominal, calculer :
Les pertes mécaniques, la puissance utile et le rendement du moteur.
1.2.Calculer la constante k liant la f.é.m E à la fréquence Ω par E = kΩ. Montrer que le moment Tem du couple
électromagnétisme est égal à kI ( I : intensité du courant dans l’induit)
1.3. Calculer la vitesse Ωv en rad.s-1 du moteur et l’intensité Iv du courant dans son induit, à vide sous la tension
nominale U = 65 V.
1.4.Le moteur étant à vide et à l’arrêt, on applique brusquement la tension U = 65 V .
1.4.1. Ecrire la relation fondamentale de la dynamique pour le moteur en mouvement.
1.4.2. Etablir la relation donnant le moment du couple Tem en fonction de U, Ω et k
1.4.3. En déduire l’équation différentielle vérifiée par Ω.
1.4.4. Mettre cette expression sous la forme aErreur ! + Ω = b.
Exprimer a et b.
1.4.5. En déduire la constante de temps mécanique τm et la vitesse finale Ωvf atteinte par le
moteur ?