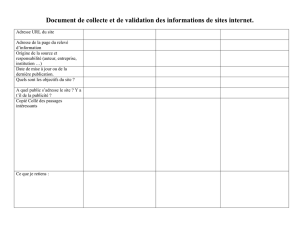
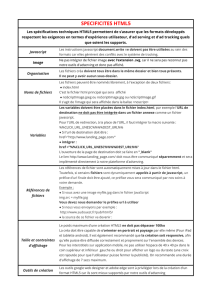
Exemples d`algorithmes 65 - Les leçons de mathématiques à l`oral

9
Exemples d’algorithmes
65
Leçon n°
Niveau Lycée
Prérequis
notions de programmation, notions d’arithmétique (PGCD), notions d’analyse
(fonctions, croissance), notions de probabilités (calcul de probabilités et loi forte
des grands nombres)
Références [169], [170], [171], [172], [?], [173]
65.1 Définition d’un algorithme
Définition 65.1 — Algorithme. Un algorithme est une suite finie d’opérations et d’instructions per-
mettant de résoudre un problème.
Exemple 65.2 On donne l’exemple d’un algorithme (un peu tordu) pour savoir ce qu’on doit faire
quand une lampe ne fonctionne plus mis sous forme d’un organigramme.
Dans ce qui va suivre, les algorithmes seront programmés grâce au logiciel de calcul formel, Xcas.
65.2 Algorithmes en arithmétique
65.2.1 Algorithme d’Euclide
Soient aet bdeux entiers relatifs. L’algorithme d’Euclide permet de calculer le plus grand commun
diviseur des entiers aet b.
R65.3 Puisque l’algorithme a pour objet le calcul d’un PGCD, il est possible de se restreindre aux entiers positifs,
un PGCD de deux entiers relatifs étant égal au PGCD de leurs valeurs absolues.
Description de l’algorithme.
— Le cas où aet best nul est trivial car PGCD(a, 0) = a.

10 Leçon n°65 •Exemples d’algorithmes
— On définit une suite (an)n∈Npar récurrence telle que a0=aet a1=bpuis tant que an+1
n’est pas nul, an+2 est défini comme le reste de la division euclidienne de anpar an+1.
On commence donc par calculer le reste de la division de apar b, qu’on note r; puis on
remplace apar b, puis bpar ret on réapplique le procédé depuis le début.
On obtient ainsi une suite, qui vaut 0à un certain rang ; le PGCD cherché est le terme précé-
dent de la suite.
Dv
•Démonstration — On montre que l’algorithme s’arrête à un moment donné.
La définition meme de la suite (an)par division euclidienne montre que, pour tout ntel que
an+1 est non nul, il existe un entier qn+2 tel que an=qn+2 ×an+1 +an+2 avec de plus
0≤an+2 < an+1 pour tout ntel que an+1 non nul. La suite d’entiers naturels (an)est donc
strictement décroissante (tant qu’elle est non nulle) à partir du rang 1, et donc vaut 0à un
certain rang. L’existence d’un dernier reste non nul est ainsi établie. •
Exemple 65.4 On calcule, par exemple, le PGCD de 1071 et de 1029 à l’aide de l’algorithme
d’Euclide :
1071 = 1029 ×1 + 42
1029 = 42 ×24 + 21
42 = 21 ×2+0
Il faut prendre le dernier reste avant le zéro donc PGCD(1071,1029) = 21.
Voici l’algorithme implémenté sur Xcas :
pgcdeuclide(a,b):={
local r;
tantque b <> 0 faire
r := irem(a,b)
a := b
b := r
ftantque
retourne(a)
}
pgcdeuclide(1071,1029)
21
65.2.2 Crible d’Eratosthène
Pour dresser la liste des nombres premiers entre 2et 100, la méthode du crible d’Eratosthène
consiste à :
— écrire la liste des nombres entiers inférieurs ou égal à 100 ;
— éliminer successivement les multiples propres de 2, de 3, . . . puis ceux de p, où pest le premier
nombre non encore élimié, etc.
Les entiers éliminés (en rouge) sont les entiers non premiers entre 2et 100. Les entiers (en vert)
sont donc les nombres premiers inférieur à 100.
R65.5

65.3 Algorithmes en analyse et probabilités 11
FIGURE 65.1 – Crible d’Erastosthène pour les entiers inférieurs ou égaux à 100
1. Pour éliminer les multiples propres de 7, commencer à 72, car les multiples inférieurs ont déjà été
éliminés.
2. Il est possible de savoir à l’avance « jusqu’où aller ». En effet, grâce au critère d’arrêt, tout entier
composé nadmet un diviseur premier ptel que :
2≤p≤n.
Si n≤10, alors √n≤√100 = 10. Tous les entier non premier sera éliminé en tant que multiple
propre de 2,3,5,7et 11.
On peut écrire un algorithme qui permet d’établir le crible d’Eratosthène (qu’on peut implémenter
sur Xcas) :
erato(n):={
local j,k,P;
P:=[seq(k,k=1..n)];
P[0]:=0;
pour jde 2jusque floor(sqrt(n)) faire
si P[j-1]>=1 alors
pour kde 2jusque floor(n/j) faire
P[j*k-1]:=0;
fpour;
fsi;
fpour;
retourne(select(x->(x>=1),P));
}:;
erato(100)
[2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97]
65.3 Algorithmes en analyse et probabilités
65.3.1 Dichotomie
Problème
Soient I= [a, b]un intervalle de Ret f:I→Rune fonction continue telle que f(a)< f(b). On
veut calculer mtel que f(m)=0. Pour cela, on construit deux suites (an)et (bn)convergentes vers
m.

12 Leçon n°65 •Exemples d’algorithmes
Principe
— On pose a0=aet b0=b.
— Soit m0le milieu de [a, b]:
— Si f(m0)>0alors on pose a1=a0et b1=m0
— Sinon on pose a1=m0et b1=b0.
— Ainsi de suite, si on veut construire le keterme de la suite, on pose mk−1le milieu de
[ak−1, bk−1]:
— Si f(mk−1)>0alors ak=ak−1et bk=mk−1
— Sinon on pose ak=mk−1et bk=bk−1.
L’algorithme sur Xcas
dicho(F,p,a,b):={
local aa,bb,k,f;
aa:=a;
bb:=b;
epsilon:=1e-100;
f:=unapply(F,x);
k:=0;
tantque evalf(bb-aa,p)>10^(-p) faire
si sign(evalf(f((bb+aa)/2),p))==sign(evalf(f(bb),p))
alors bb:=evalf((aa+bb)/2,p);
sinon aa:=evalf((aa+bb)/2,p);
k:=k+1;
fsi;
ftantque;
retourne evalf((bb+aa)/2,p)+" est la solution trouvée apres " +k+ " itérations";
}:;
dicho(x^4-x^2+x-4,5,0,5)
1.47198 est la solution trouvée apres 11 itérations
et sa version récursive :
dicho_rec(f,a,b,eps,compteur):={
si evalf(b-a)<eps alors 0.5*(b+a),compteur+1
sinon si f(a)*f(0.5*(b+a))>0
alors dicho_rec(f,0.5*(b+a),b,eps,compteur+1)
sinon dicho_rec(f,a,0.5*(b+a),eps,compteur+1)
fsi
fsi
}:;
dicho_rec(x->x^4-x^2+x-4,0,5,10^(-6),0)
(1.47198408842,24)
Le théorème des valeurs intermédiaires
Théorème 65.6 — Théorème des valeurs intermédiaires. Soient Iun intervalle, aet bdans Itels que
a<b. Soit fune application continue sur l’intervalle I. Soit λ, un réel compris entre f(a)et f(b).
Alors il existe (au moins) un réel cdans [a , b]tel que f(c) = λ.

65.3 Algorithmes en analyse et probabilités 13
Dv
•Démonstration du théorème 65.6 —Supposons f(a)< f(b). Nous allons construire deux
suites adjacentes (an)n∈N∗et (bn)n∈N∗par l’algorithme suivant :
— Si le milieu mde l’intervalle [a , b]est tel que f(m)≥malors on pose a1=aet b1=m.
— Sinon, on pose a1=met b1=b.
On recommence le découpage :
— Si le milieu mde l’intervalle [a1, b1]est tel que f(m)≥λalors on pose a2=a1et
b2=m.
— Sinon, on pose a2=met b2=b1.
On a ainsi :
a≤a1≤a2≤b2≤b1≤bet f(a2)≤λ≤f(b2).
a
f(a)
b
f(b)
?
λ
Cf
b1
a1b1
b2
?
En réitérant le procédé, on construit ainsi une suite de segments emboîtés a:
[a , b]⊃[a1, b1]⊃ ··· ⊃ [an, bn]⊃ ··· .
De plus, par construction, la longueur de [an, bn]est b−a
2n. Les segments [an, bn]ont donc
des longueurs qui tendent vers 0. Les suites (an)n∈N∗et (bn)n∈N∗sont donc adjacentes.
Notons cleur limite commune (ce réel cest dans l’intervalle [a , b]). Montrons que f(c) = λ.
On a, pour tout n∈N∗:
f(an)≤λ≤f(bn)
et par passage à la limite :
lim
n→+∞f(an)λ≤lim n→+∞f(bn).
Or, fest continue en cdonc :
f(c)≤λ≤f(c)
et ainsi f(c) = λ. On a bien montré qu’il existe un réel cdans [a , b]tel que f(c) = λ. •
a. Il s’agit d’une méthode de dichotomie.
R65.7
1. Le théorème des valeurs intermédiaires nous dit que l’équation f(x) = λ(f(a)< λ < f(b)) admet au
moins une solution dans [a , b].