correctionds2 20112012

EXERCICE I : FERMENTATION DANS LE VIN (8 points)
0,25 pt sur l’ensemble de l’exercice pour les chiffres significatifs.
A – Première partie: détermination du degré alcoolique d'un vin
I Questions préliminaires (0,75 pts)
1. Les demi-équations électroniques associées aux couples: CH
3
CHO / CH
3
CH
2
OH et NAD
+
/ NADH sont:
oxydation de l'éthanol: CH
3
CH
2
OH = CH
3
CHO + 2 e
–
+ 2 H
+
réduction du NAD
+
: NAD
+
+ 2e
–
+ H
+
= NADH
CH
3
CH
2
OH + NAD
+
= CH
3
CHO + NADH + H
+
On retrouve bien l'équation (1) donnée dans l'énoncé.
Au cours de la réaction (1), l'éthanol CH
3
CH
2
OH est oxydé en éthanal CH
3
CHO avec libération de deux électrons
tandis que NAD
+
est réduit en NADH avec capture de deux électrons. On a transfert de deux électrons entre
l'éthanol et NAD
+
. (0,25 pour chaque ½ équation)
2. Un catalyseur est une espèce chimique capable d'accélérer une réaction chimique: le catalyseur n'intervient pas
dans l'écriture de l'équation de la réaction, car en fin de réaction il se retrouve inchangé. Il s'agit ici d'une catalyse
enzymatique. (juste pour le fait d’accélerer la réaction)
II. Étalonnage du spectrophotomètre (3,75 pts)
1. Lors du réglage initial du spectrophotomètre, la valeur de l'absorbance de la solution de référence doit être
nulle. On dit qu'on réalise "le blanc" du spectrophotomètre (0.25 pt réponse)
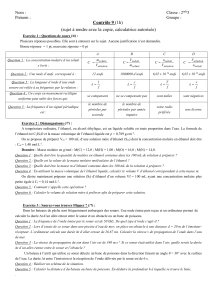
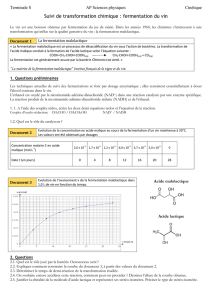
2. Graphe A = f(C
m
) (0,5 pt pour la courbe dont 0,25 pt pour la qualité de la courbe + 0,25 légende+ axe des
ordonnées et des abscisses corrects)
3. Le graphe est une droite qui passe par l'origine du repère. L'absorbance A est donc proportionnelle à la
concentration massique C
m
, soit: A = k . C
m
avec k coefficient directeur de la droite.(0,25 justification)
À l'aide des points (0; 0) et (300 ; 0,48), on détermine: k =
_
_
0,48 0
300 0
= 1,6×
××
×10
–3
L.mg
–1
. (0,25 pt la valeur)
III – Préparation et dosage de l'éthanol contenu dans le vin
1. Solution D: Échantillon E:
C
D
= ? C
E
= ?
V
D
= 1 mL V
E
= 50 mL
Au cours de la dilution de la solution D pour préparer l'échantillon E, la quantité d'éthanol est conservée, donc:
Absorbance en fonction de la concentration massique
0
0,1
0,2
0,3
0,4
0,5
0 50 100 150 200 250 300
C
m
(mg.L
-1
)
A
0,5 pt
0,25
pt
0,25
pt
0,50
pt
0,5
pt

n
D
= n
E
⇔ C
D
.V
D
= C
E
.V
E
⇔
50
1
== E
D
D
EV
V
C
C
⇔
50
=
D
E
C
C
L'échantillon correspond donc à une dilution au 1/50
e
de la solution D. (0,5 démonstration)
2. On a A
e
= 0,30 donc d'après la relation précédente: C
m,e
=
e
A
k
C
m,e
=
_
3
0,30
1,6.10
≈1,9.10
2
mg.L
-1
. (0,25 méthode + 0,25 valeur : si méthode que graphique 0,25 pt)
On aurait pu utiliser le graphe A = f(Cm) du II.2. mais cette méthode serait moins précise.
3. a) La solution D ayant été diluée 50 fois, il vient: C
m,D
= 50 ×C
m,e
C
m,D
= 50 × 1,9.10
2
≈9,4×10
3
mg.L
–1
≈9,4 g.L
–1
(calcul effectué avec la valeur de C
m,e
stockée)
(0,25 formule littérale + 0,25 pt la valeur)
3.b) Le distillat de vin (20 mL) ayant été dilué 10 fois pour préparer 200 mL de solution D, la concentration
massique du vin est en éthanol est: C
m,vin
= 10 ×C
m,D
C
m,vin
= 10 × 9,4 ≈94 g.L
–1
. (0,25 formule littérale + 0,25 pt la valeur)
4. 1 L de vin contient 94 g d'éthanol donc 100 mL de vin contient 9,4 g d'éthanol.
Or la masse volumique de l'éthanol étant µ(ol) = 0,80 kg.L
-1
= 8,0×10
2
g.L
–1
, le volume d'éthanol V(ol) en L
correspondant à une masse m(éthanol) = 9,4 g est:
V(ol) =
2
( ) 9,4
( ) 8,0 10
m ol
ol µ
=×
≈1,2.10
-2
L = 12 mL
Ainsi d'après la définition du degré alcoolique, ce vin a un degré alcoolique de 12 % vol.(0,25 formule +
explications +0,25 valeur)
B – Deuxième partie: cinétique de la fermentation malolactique (3,25 pts)
1. La concentration molaire en acide malique [acide malique] et concentration massique en acide malique C
m
sont
liées par la masse molaire M selon:
[acide malique ] =
n
V
or n =
m
M
donc [acide malique ] =
.
m
M V
et C
m
=
m
V
donc [acide malique] (t) =
M)t(C
m
La masse molaire de l'acide malique est: M = 4 ×M(C) + 5 × M(O) + 6 × M(H)
M = 4 × 12,0 + 5 × 16,0 + 6 × 1,0 = 134,0 g.mol–1
D'où la relation: [acide malique] (t) =
134
)t(C
m (0,5 démonstration)
À t = 0, on a Cm(0) = 3,5 g.L–1 donc [acide malique] (0) =
134
53 ,
= 2,6×
××
×10
–2
mol.L
-1
.
La quantité initiale d'acide malique à l'instant initial pour 1 L de vin est donc:
n
acide malique
(t = 0) = 2,6×
××
×10
–2
mol (0,25 valeur)
2. Le tableau d'avancement de la réaction (en mol) est:
acide malique = acide lactique + CO
2
État initial (t=0) 2,6×10
-2
0 0
En cours t 2,6×10
-2
– x(t) x(t) x(t)
A l'instant t, la quantité d'acide malique restante est: n
acide malique
(t) = 2,6.10
-2
– x(t) (0,25 l’expression+0.25
tableau)
D'où: x(t) = 2,6×10
–2
– n
acide malique
(t)
3.a) La vitesse volumique v, à l'instant t, de la réaction est définie par: v =
1.
t
dx
V dt
avec V le volume du mélange réactionnel (en L), x en mol, et t en jours (ici) (0,25 pt rappel de la formule)
0,5
pt
0,5
pt
0,5
pt
0,5
pt
0,5
pt
0,75
pt
0,5
pt

Or le terme
t
dx
dt
est égal au coefficient directeur de la tangente au graphe x(t) à l'instant t. Pour évaluer la
vitesse de réaction à l'instant t, il suffit de calculer le terme
t
dx
dt
et de multiplier ce terme par 1 / V (0,25 pt
méthode)
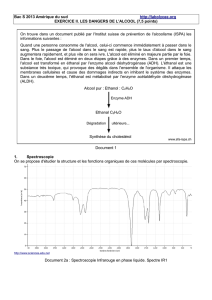
3.b) La vitesse volumique est proportionnelle au coefficient directeur de la tangente au graphe x(t) à l'instant t. Au
cours du temps, on observe que ce coefficient directeur diminue donc la vitesse volumique de la réaction diminue
au cours du temps. Ceci est la conséquence de la diminution de la concentration en réactifs qui est un facteur
cinétqiue (0,25 pt réponse + 0.25 pt justification)
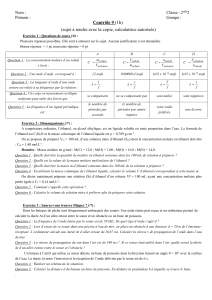
4. Le temps de demi-réaction t
1/2
est la durée pour laquelle l'avancement x atteint la moitié de sa valeur finale x
f
:
x(t
1/2
) = x
f
/ 2 (0,5 pt définition)
Or ici on a x
f
= 0,026 mol pour t = 28 jours donc x(t
1/2
) = x
f
/ 2 = 0,013 mol.
Graphiquement on obtient t
1/2
= 6,1 jours. (0,25 justification + 0,25 valeur)
EXERCICE II :La physique au service de l’acoustique des théâtres antiques (12 points)
1. On appelle onde mécanique progressive, le phénomène de propagation d’une perturbation dans un milieu
matériel élastique sans transport global de matière mais avec transport d’énergie (0,25 pt pour l’aspect
mécanique + 0.25 pt l’aspect progressif)
2. L’onde sonore se propage dans l’air dans un espace à trois dimensions.
B. Simulation d’un théâtre à l’aide d’une maquette
1. Utilisation d’un émetteur ultrasonore
1.1. La longueur d’onde λ est la distance parcourue par une onde périodique pendant une durée égale à une
période T (définition complète exigée)
1.2. v
T
λ
=
= λ.f donc
v
f
λ =
ou λ=v.T (0,25 pt une des 2 formules)
1.3. D’après le texte, la célérité des ultrasons v
US
est égale à celle des sons de la voix v
Son
.
Son
Son
Son
v
f
λ = et
Son
US
US
v
f
λ =
0
0,005
0,01
0,015
0,02
0,025
0,03
0 5 10 15 20 25 30
x en mol
t en jours
t
1/2
0,5
pt
0,5
pt
1 pt
0,5
pt
0,25
pt
0,5
pt
0,25
pt

Et les fréquences des sons audibles sont telles que 20 Hz < f
son
< 20 × 10
3
Hz, tandis que fréquence des ultrasons :
f
US
> 20×10
3
Hz.
f
US
> f
Son
donc 1/f
US
< 1/f
Son
ce qui implique en multipliant cette inégalité par v
son
: λ
US
< λ
Son
.
Ainsi la longueur d’onde des ultrasons est inférieure à la longueur d’onde moyenne des sons de la voix. (0,5 pt
démonstration)
1.4. Les dimensions de la maquette du théâtre sont réduites. Il faut alors que les longueurs d’onde des sons utilisés
soient réduites du même facteur.
La relation v = λ
λλ
λ.f montre que pour v constante si λ diminue alors f augmente. Les fréquences des ultrasons étant
supérieures aux fréquences des ondes sonores, on utilise les ultrasons dans le cadre de la simulation avec une
maquette (1 des 2 explications acceptées)
1.5. Un milieu est dispersif si la célérité des ondes qui s’y propagent dépend de la fréquence. Ce qui revient à dire
que la célérité varie quand la fréquence de l’onde varie. (0,25 pt définition).
1.6. La célérité des ondes ultrasonores dans l’air est égale à celle des ondes sonores(340 m.s
−1
) : l’air n’est pas un
milieu dispersif pour les ondes sonores et ultrasonores. Sauf cas particulier pour des ondes sonores de grande
amplitude (tonnerre)ou dans ce cas particulier l’air est dispersif (pas le cas ici). (0,5 pt justification +0,5 pt réponse)
2. Influence d’un plafond
2.1.
D
v
=
τ
donc
D
v
τ =
soit
1
3
2
0,68 6,8 10
2,0 10
340 3,40 10
−
−
×
τ = = = ×
×
s. (0,25 pt formule
+ 0,5 pt valeur)
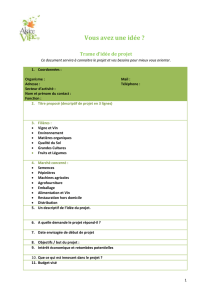
2.2. On constate que l’amortissement des échos est plus marqué
dans l’expérience 2 (couvercle + moquette) que dans l’expérience 1
(couvercle). L’expérience 3 (sans le couvercle) montre qu’il n’y a
quasiment plus d’échos dans le signal reçu, les échos sont très
amortis. (0,5 pt pour chaque constat = 1 pt)
2.3. Plus les échos sont amortis et meilleure est la qualité du son perçu par le spectateur. Ainsi l’absence de
couvercle (exp. 3) est plus intéressante d’un point de vue acoustique.(0,25 pt réponse + 0,5 pt justification)
2.4. Les plafonds des salles de concert sont recouverts de dalles alvéolées absorbantes afin de diminuer
l’amplitude des échos sur le plafond. (0,25 pt réponse)
3. Rôle du mur : simulation à l’aide d’une cuve à onde
3.1. Les ondes créées à la surface de l’eau sont transversales car la direction de la perturbation (verticale) est
perpendiculaire à la direction de propagation de l’onde (horizontale).(0,25 pt réponse + 0,5 pt justification)
3.2. Les vaguelettes à la surface de la cuve sont moins visibles lors de l’expérience 1 (mur plan) que lors de
l’expérience 2 (mur plan alvéolé). On peut penser qu’elles possèdent une plus faible amplitude. Ainsi, l’intensité
des ondes sonores reçues par les spectateurs dans les gradins, est plus faible avec un mur plan qu’avec un mur
alvéolé (0,5 pt justifications + 0,5 pt constat)
3.3.
avec
couvercle
avec couvercle
« moquette »
sans
couvercle
0,5
pt
0,25
pt
0,25
pt
1 pt
0,75
pt
1 pt
0,75
pt
0,2
5
pt
0.75
pt
1 pt

(0,5 pt méthode + 1 pt calcul détaillé avec la valeur)
3.4. Le pulpitum est alvéolé du coté de l’orchestre grâce à la présence des niches et des colonnes. Le son de
l’orchestre n’est pas amorti par le pulpitum. (= expérience 2 où le vibreur est équivalent à l’orchestre)
Du coté de la scène, le pulpitum est plan. Dès lors, les sons de l’orchestre réfléchis par le mur situé derrière la
scène sont amortis par la face plane du pulpitum (= expérience 1).( 0,25 pt pour chaque comparaison avec les
expériences=0,5 pt)
3.5.1. B étant le symétrique de A par rapport au mur, on a : AB = 2d. (0,5 pt formule)
3.5.2.
2d
v
t
=
∆
donc ∆t =
2d
v
( 0,5 pt formule)
3.5.3. Il faut que ∆t < 1/25 s donc :
2d 1
v 25
≤ doit
v
d
50
≤
Finalement pour d = d
max
et v = 350 m.s
−1
on a :
max
v 350
d
50 50
= = =
7,0 m.
(0,5 raisonnement avec formule + 0,5 pt valeur)
Valeur cohérente avec celle donnée dans la conclusion (6,60 m).
Cliché réel
2,5 cm ⇔ 10 cm
7λ
cliché
= 2,5 cm ⇔ 7λ
réel
= ?
Donc 7λ
réel
= 2,5 × 10 / 2,5 = 10 cm
λ
λλ
λ
réel
= 10 / 7 ≈ 1,4 cm
(1,4 × 7 = 9,8)
7λ
cliché
= 2,5 cm
1,5
pt
0,5
pt
0,5
pt
0,5
pt
1 pt